Формула Стірлінга
Розглядаючи|розглядуючи| комбінаторні завдання|задачі|, ми часто стикаємося з|із| факторіалами. Факторіал – це функція, що дуже швидко росте|зростає|, вона росте|зростає| швидше за експоненту. При достатньо|досить| великих n (n > 10) для визначення факторіалу n! Можна використовувати наближену формулу Стірлінга:
. (5.5)
Погрішність такого наближення визначається формулою
. (5.6)
Неважко|скрутно| показати, що
.
Підстановки
Взаємно
однозначна функція
називається підстановкою
на
.
Якщо множина|безліч|
кінчена (
),
то можна вважати|лічити|,
що
.
В цьому випадку підстановку
зручно задавати таблицею з|із|
двох рядків. У першому рядку – значення
аргументів, в другій – відповідне
значення функції. Нижче приведені
приклади|зразки|
довільних дискретних підстановок
і
:
, 
.
Добичею|добутком|
підстановок
і
називається їх суперпозиція
.
Суперпозиція
– це результат послідовного
застосування|вживання|
двох підстановок. Твір|добуток|
двох приведених вище підстановок рівний
.
Для
обчислення|підрахунку|
результату був використаний наступний|такий|
алгоритм. Перший по номеру елемент
підстановки
рівний 5. Тому звертаємося|обертаємося|
до п'ятого по номеру елементу підстановки
і бачимо, що він також рівний 5.
Означає|значить|,
перший елемент твору|добутку|
буде рівний 5.
Другий елемент рівний 2. Тому звертаємося|обертаємося| до другого елементу і бачимо, що він рівний 1. Останнє значення приймаємо як другого елементу добичі|добутку| . Діючи аналогічним чином, одержуємо|отримуємо| всі останні елементи добичі|добутку|.
Як можна бачити, добич|добуток| підстановок також є|з'являється,являється| підстановкою. Добич|добуток| підстановок визначена для підстановок однакового розміру. Добич|добуток| підстановок в загальному|спільному| випадку не володіє властивістю комутативності, тобто|цебто|
.
Одинична|поодинока|
(або тотожна)
підстановка – це підстановка
така, що
.
Наприклад:
.
Зворотна
підстановка
по відношенню до підстановки
– це підстановка, що задовольняє
співвідношенню:
. (5.7)
Таблицю зворотної підстановки можна одержати|отримати|, якщо просто поміняти місцями рядки таблиці початкової|вихідної| підстановки. Наприклад:
, 
.
Підстановки
можна представляти|уявляти|
в графічній формі, проводячи стрілки
від кожного елементу
до елементу
.
Приклад|зразок| 5.6. Задана постановка
.
Графічне представлення цієї підстановки показане на мал. 5.2.
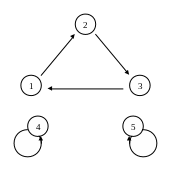
Мал. 5.2
У сучасній математиці операції, алгебри, застосовують не тільки|не лише| до скалярних чисел, але і до інших об'єктів. Наприклад, до матриць або підстановок. Безліч різних об'єктів, для яких визначені відповідні операції алгебри, називаються алгеброю в широкому сенсі|змісті,рації| цього слова. Якщо визначені чотири дії: складання, віднімання, множення і ділення|поділка,розподіл,поділ| – така алгебра називається полем.
Таким чином, звичайна|звична| алгебра (у вузькому сенсі|змісті,рації| цього слова) є|з'являється,являється| полем. Якщо операція ділення|поділки,розподілу,поділу| в алгебрі не визначена, така алгебра називається кільцем. Якщо визначена тільки|лише| одна операція, то алгебра називається групою. Причому, ця операція повинна володіти властивістю асоціативності:
,
сама алгебра повинна мати одиничний|поодинокий| елемент з|із| властивістю:
,
і для
кожного об'єкту
мати зворотний елемент
:
.
Тепер ми можемо стверджувати, що безліч підстановок утворюють групу щодо|відносно| операції суперпозиції. Ця група називається симетричною ступеню|мірі| n.
Цикл – це послідовність елементів, така що
Цикл довжини 2 називається транспозицією.
Якщо
прийняти угоду, що елементи верхнього
рядка (аргументи) завжди розташовуються
в певному порядку|ладі|
(наприклад, за збільшенням), то верхній
рядок можна не указувати|вказувати|
– підстановка однозначно визначається
нижнім рядком. Такі підстановки в один
рядок називаються перестановками.
Перестановку елементів
позначатимемо
|значитимемо|,
де усі
– різні числа з|із|
діапазону
.
Якщо в
перестановці
для елементів
і
має місце нерівність
при, то пара
називається інверсією.
Позначимо
– число
інверсій в
перестановці
.
Теорема 5.5. Довільну підстановку можна представити|уявити| у вигляді суперпозиції транспозицій сусідніх елементів.
Доказ.
Хай|нехай|
.
Переставимо 1 на перше місце,
міняючи|змінюючи,замінюючи|
її місцями з|із|
сусідніми зліва|ліворуч|
елементами. Позначимо послідовність
цих транспозицій через
.
При цьому всі інверсії, в яких брала
участь 1, пропадуть. Потім переставимо
2 на друге місце і т.д. Таким чином,
і по властивості групи, причому
.
Слідство|наслідок|. Всяке|усяке| сортування може бути виконане перестановкою сусідніх елементів.
Такий метод сортування відомий як бульбашковий метод. Цей метод простий, але|та| є|з'являється,являється| далеко не найефективнішим алгоритмом сортування.