2. Доказать, что множество перестановок с четным числом инверсий образует группу.

3. По заданной матрице смежности определить число циклов длины 3 и длины 4. Записать матрицу инцидентности и матрицу фундаментальных циклов.

4. Теоретический вопрос: Преобразование Лапласа и z-преобразование.

ВАРИАНТ № 27

1. Докажите методом математической индукции, что сумма первых квадратов равна

.

2. Используя метод операционного исчисления, решить следующее дифференциальное уравнение: с нулевым начальным условием .

3. Найти хроматический полином показанного на рисунке графа.

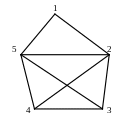
4. Теоретический вопрос: Дайте определение ориентированного графа.

ВАРИАНТ № 28

1. Докажите следующую формулу:

.

2. Доказать, что для сочетаний справедлива формула: .

3. Построить матрицу смежности и матрицу инцидентности приведенного на рисунке графа.

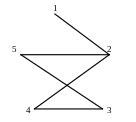
4. Теоретический вопрос: Дайте определение неориентированного графа.

ВАРИАНТ № 29

1. Докажите, что .

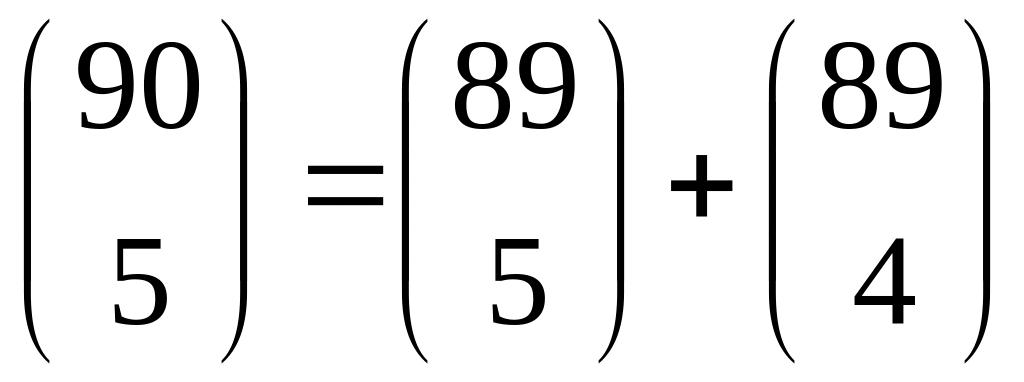2. Найти решение рекуррентного уравнения с начальными условиями .

3. Найти компоненты сильной связности графа.

4. Теоретический вопрос: Дайте определение матрицы смежности и матрицы инцидентности графа.

ВАРИАНТ № 30

1. Докажите, что .

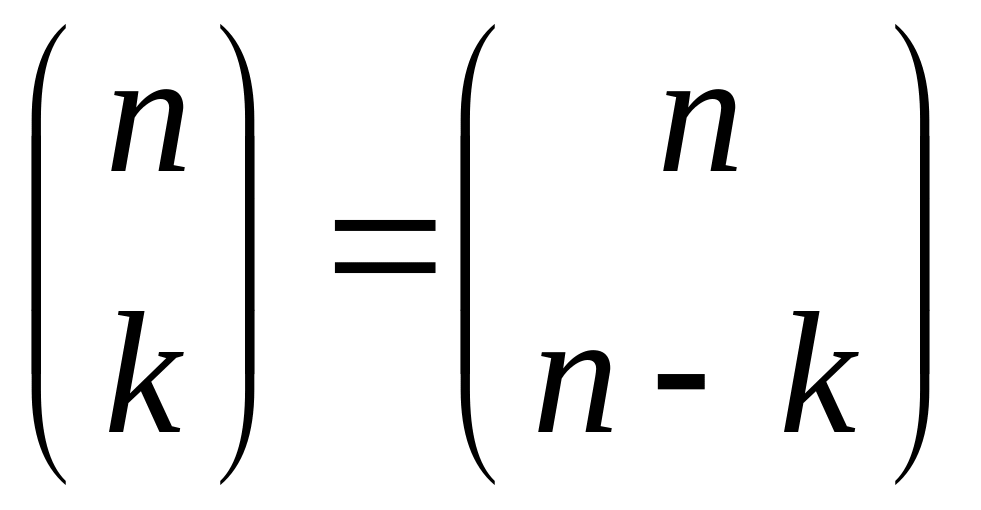2. Решите рекуррентное уравнение с начальными условиями: .

3. Построить матрицу смежности и матрицу инцидентности приведенного на рисунке графа.

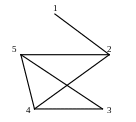
4. Теоретический вопрос: Дайте определение взвешенного графа.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. – 304 с.

2. Кирсанов М.Н. Графы в Maple. Задачи, алгоритмы, программы. – М.: ФИЗМАТЛИТ, 2007. – 168 с.

3. Владимирский Б.М., Горстко А.Б., Ерусалимский Я.М. Математика. Общий курс. – СПб.: Издательство «Лань», 2004. – 960 с. (глава V. Дискретная математика).

4. Фудзисава Т., Касами Т. Математика для радиоинженеров: Теория дискретных структур: Пер. с япон. – М.: Радио и связь, 1984. – 240 с.

5. Lovasz L., Vesztergombi K. Discrete Mathematics. – Yale: by Yale University Publishing, 1999. – 139 p.

6. Яблонский С. В. Введение в дискретную математику. – М.: Наука, 1986.

7. Мендельсон Э. Введение в математическую логику. М.: Наука, 1984.

8. Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по курсу дискретной математики – М.: Наука. – 1992.

9. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990.

10. Нефедов В. Н., Осипова В. А. Курс дискретной математики. – М.: Издательство МАИ, 1992.

11. Булос Дж., Джеффри Р. Вычислимость и логика. М.: Мир, 1994.

12. Курант Р., Роббинс Г. Что такое математика? – М.: МЦНМО, 2007. – 568 с.