1. В спортивном магазине продают рубашки 5-ти различных цветов, шорты 4-х различных цветов и носки 3-х различных цветов. Сколько различных комбинаций форм можно составить в этом случае?

2. Найти число сочетаний из 8 различных элементов по 5 с повторениями и без повторений.

3. По заданной матрице смежности определить число циклов длины 3 и длины 4. Записать матрицу инцидентности и матрицу фундаментальных циклов.

4. Теоретический вопрос: Размещения и сочетания без повторений.

Вариант № 17

1. Мы имеем 20 различных подарков, которые нужно распределить между 12 детьми. Мы не будем требовать, чтобы каждый ребенок получил что-нибудь. Может случиться, что все подарки получит один ребенок. Определите количество комбинаций распределений подарков в этом случае.

2. Найти производящую функцию последовательности чисел: 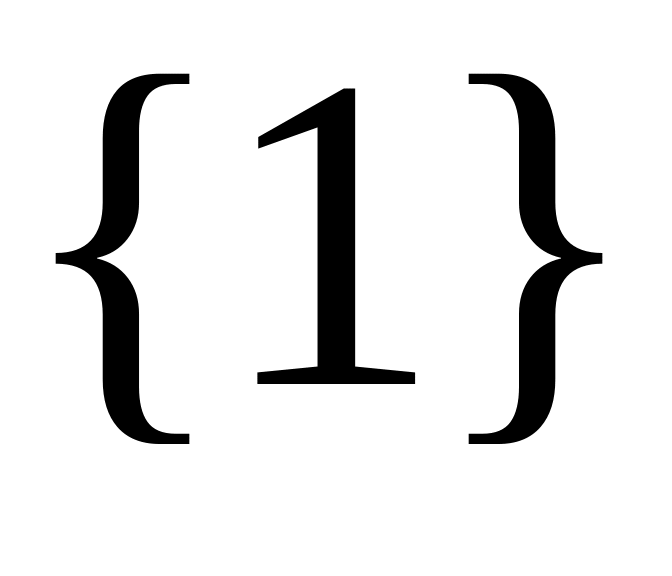и .

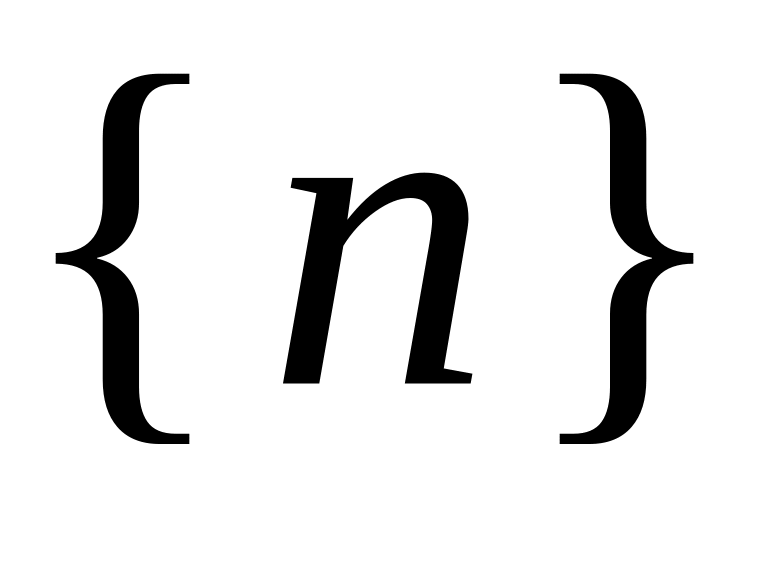3. На рисунке приведен орграф. Сколько в нем маршрутов длиной 3?

4. Теоретический вопрос: Размещения и сочетания с повторениями.

Вариант № 18

1. Мы имеем 20 сортов подарков, причем имеется большой запас каждого. Мы хотим распределить эти подарки между 12 детьми. Не требуется, чтобы каждый ребенок получил что-нибудь, однако ни один ребенок не должен получить копию подарка (подарки должны быть разными). Сколько существует вариантов распределения подарков в этом случае?

2. Докажите следующую формулу: .

3. Записать десятичный код дерева с корнем в вершине 3.

4. Теоретический вопрос: Формула Стирлинга.

ВАРИАНТ № 19

1. n парней и n девушек хотят потанцевать. Сколько комбинаций пар существует, когда они танцуют одновременно (предполагается, что в каждой паре находятся представители разного пола)?

2. Найти производящую функцию для биномиальных коэффициентов.

3. Записать код Прюфера для дерева.

4. Теоретический вопрос: Подстановки.

ВАРИАНТ № 20

1. Докажите неравенство .

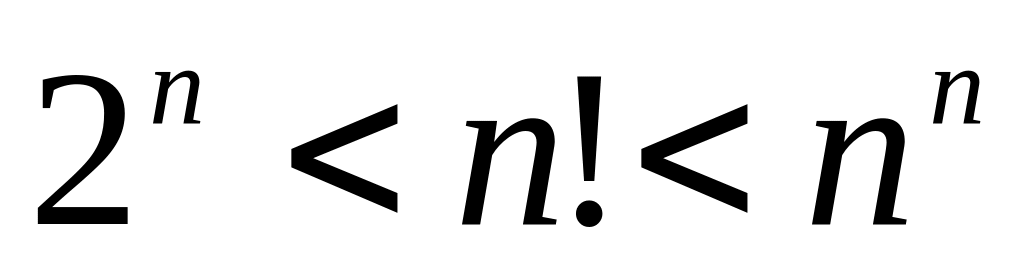2. Докажите тождество: 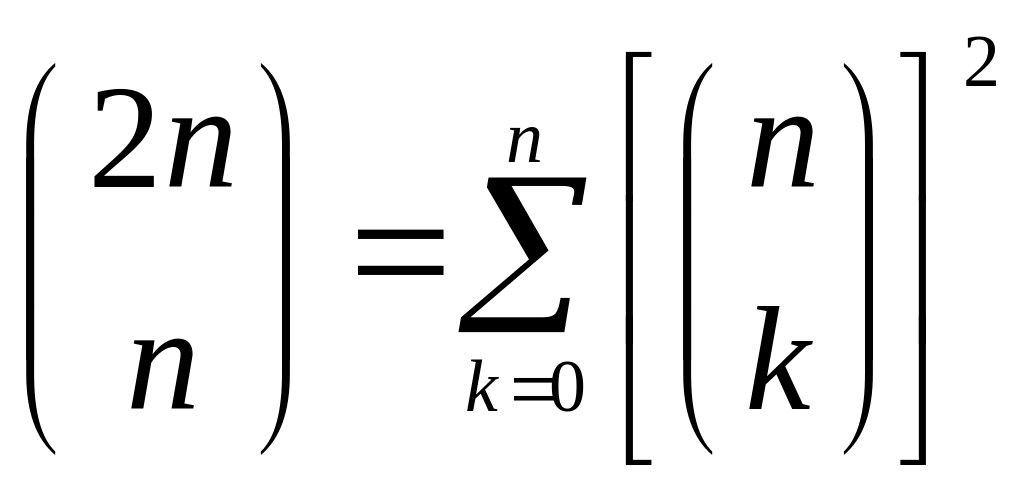– с использованием производящих функций.

3. По заданной матрице смежности определить число циклов длины 3 и 4. Записать матрицу инцидентности и матрицу фундаментальных циклов.

4. Теоретический вопрос: Алфавитное кодирование.

ВАРИАНТ № 21

1. Чему равно множество всех подмножеств конечного множества с кардинальным числом 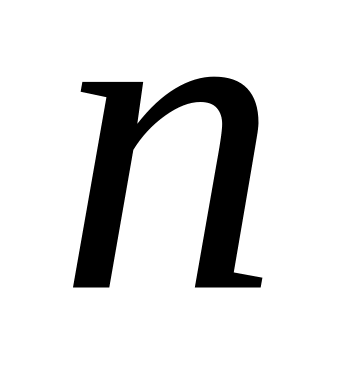? Обоснуйте свой ответ.

2. Решите рекуррентное уравнение 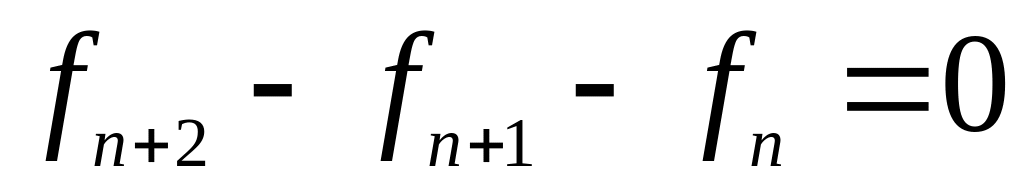с начальными условиями: .

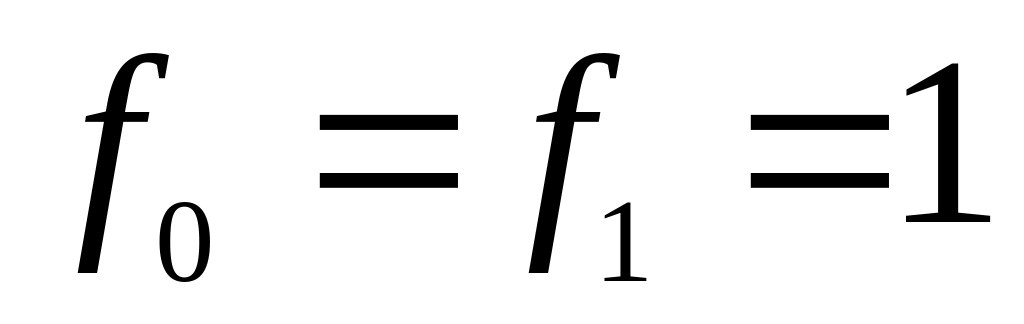3. Найти компоненты сильной связности графа.

4. Теоретический вопрос: Числа Фибоначчи.

ВАРИАНТ № 22

1. Что больше или 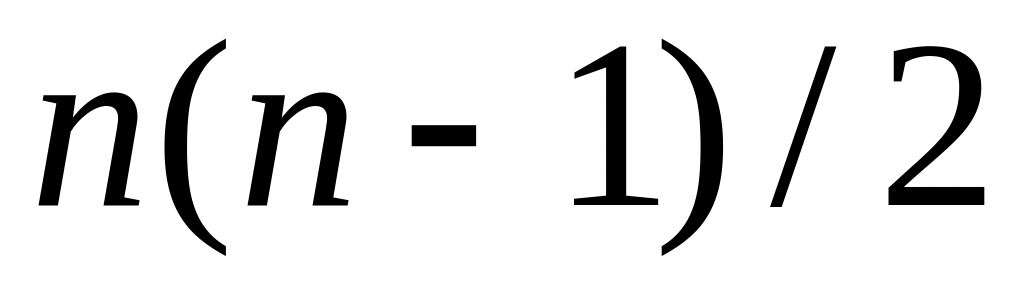? Обоснуйте свой ответ.

2. Найти решение рекуррентного уравнения 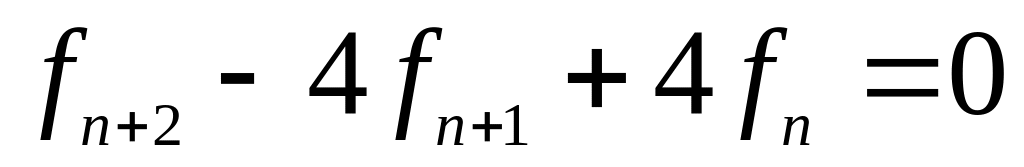с начальными условиями .

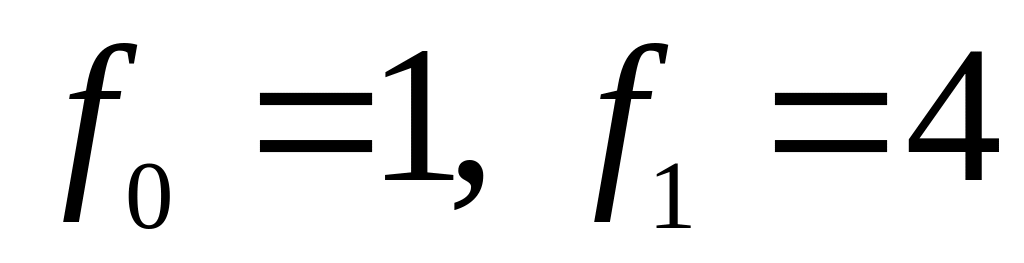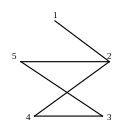
3. Построить реберный граф для заданного на рисунке графа.

4. Теоретический вопрос: Простые числа.

ВАРИАНТ № 23

1. Что больше 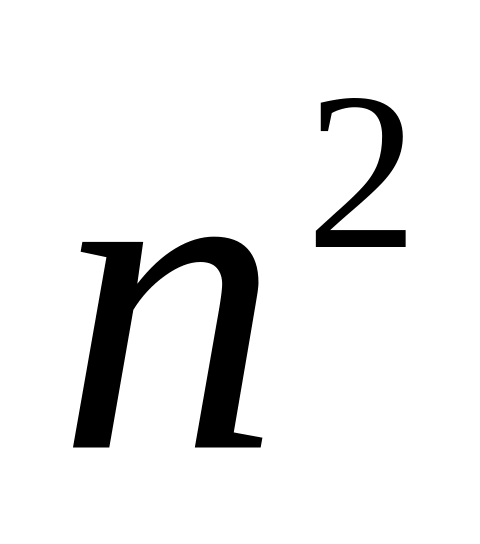или ?

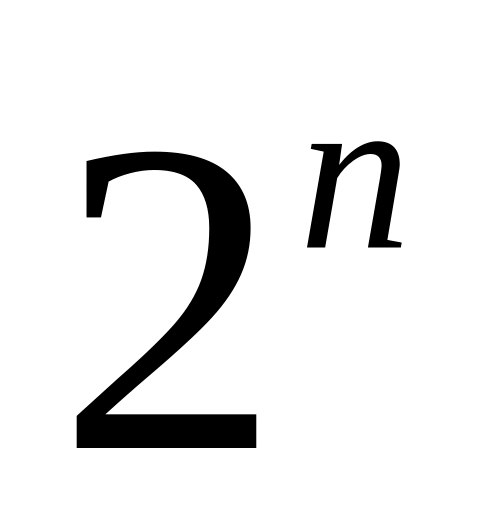2. Докажите, что для , .

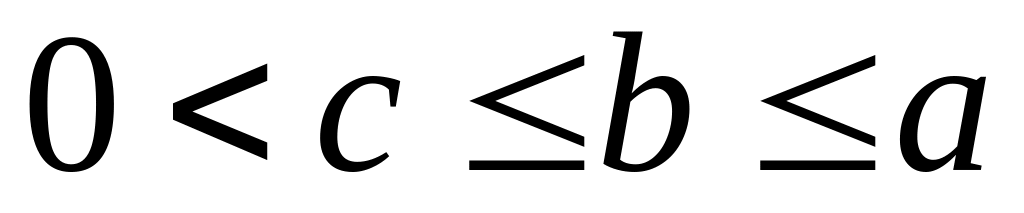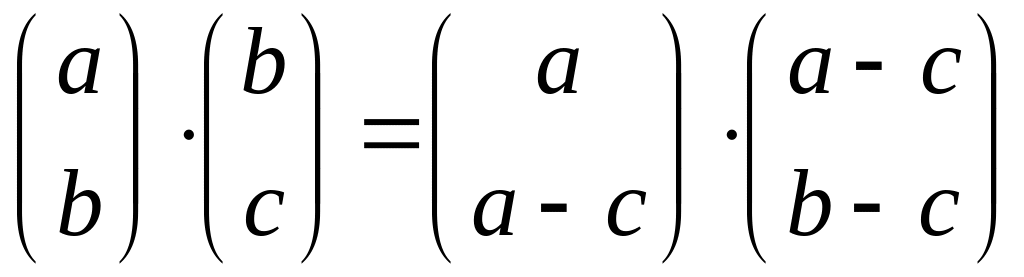3. Дан взвешенный орграф. Найти кратчайший путь из вершины A в B.

4. Теоретический вопрос: Рекуррентные уравнения.

ВАРИАНТ № 24

1. Используя метод математической индукции, докажите, что 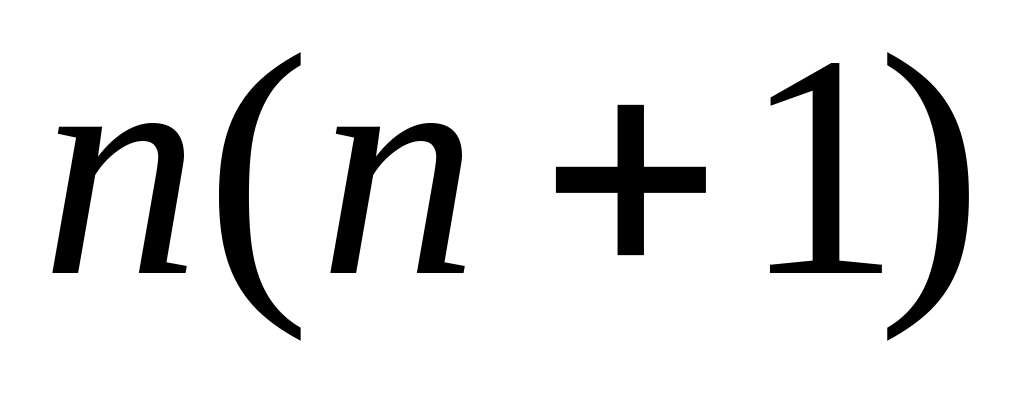является четным числом при каждом неотрицательном целом .

2. Докажите тождество для чисел Фибоначчи:

.

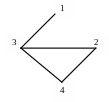
3. Дан взвешенный граф. Найти число остовов графа минимального веса (экстремальное дерево).

4. Теоретический вопрос: Производящие функции.

ВАРИАНТ № 25

1. Докажите с помощью метода математической индукции, что сумма первых положительных целых чисел равна .

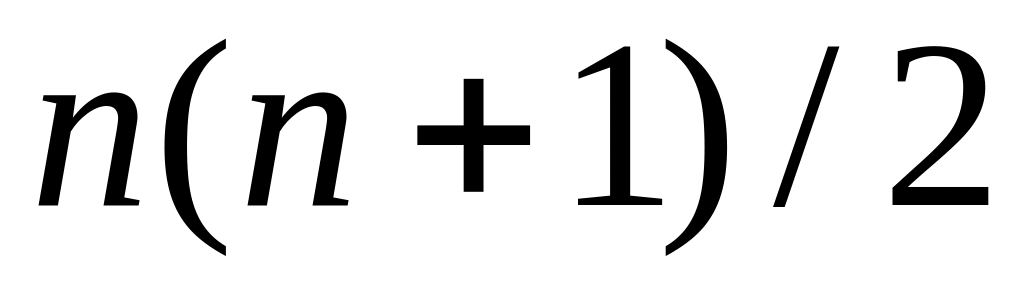2. Используя метод операционного исчисления, решить следующее дифференциальное уравнение: с нулевым начальным условием .

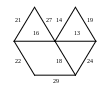
3. Найти матрицу смежности и матрицу инцидентности показанного на рисунке графа.

4. Теоретический вопрос: Обыкновенные дифференциальные уравнения.

ВАРИАНТ № 26

1. Докажите следующее тождество методом математической индукции:

.