1. Запишите множество, для которого 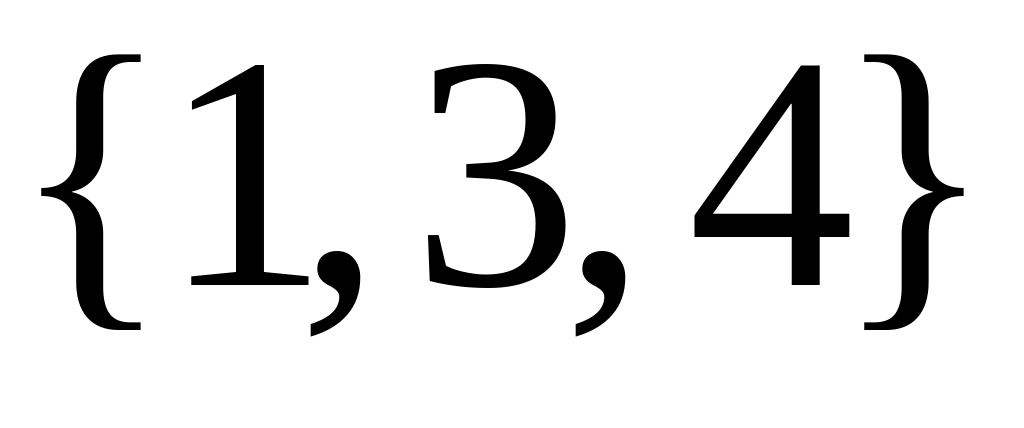и 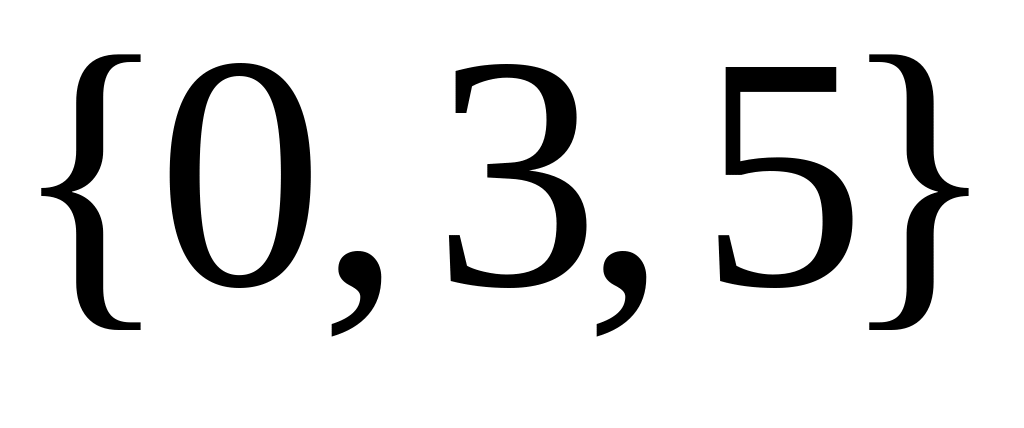являются подмножествами. Найдите такое множество, которое содержит минимально возможное количество элементов при этом.

2. Докажите тождество для чисел Фибоначчи: .

3. Записать десятичный код дерева с корнем в вершине 3.

4. Теоретический вопрос: Способы задания множеств.

ВАРИАНТ № 8

1. Найдите объединение трех множеств 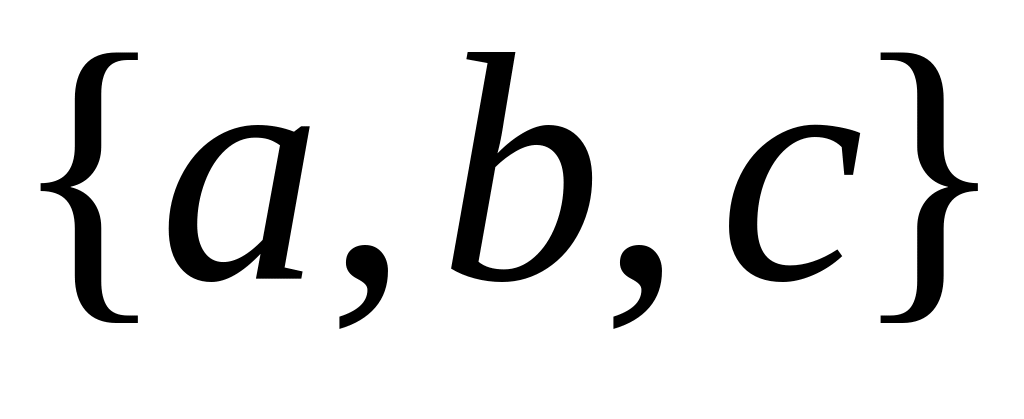, 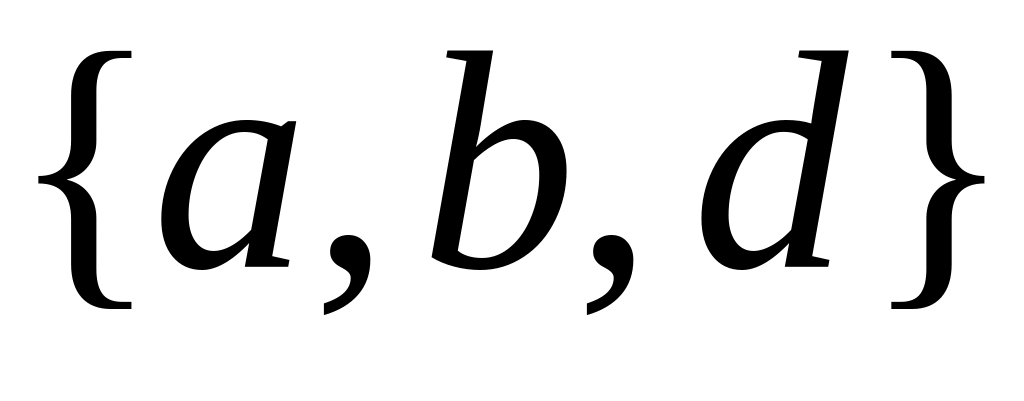и 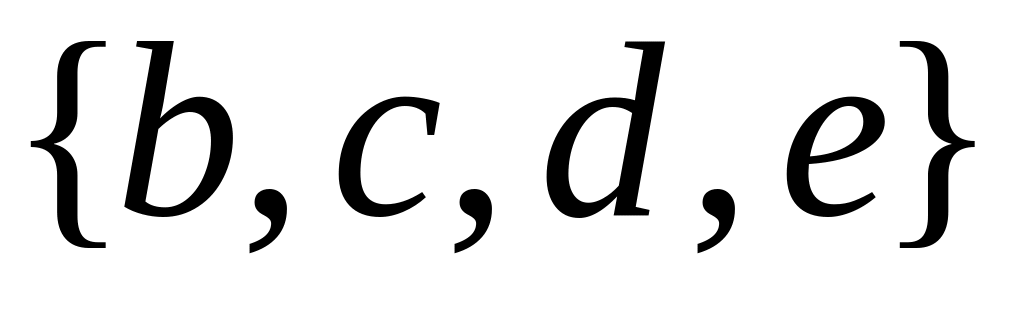. Прежде найдите объединение первых двух множеств, а затем их объединение с третьим. Затем найдите объединение последних двух множеств, и потом их объединение с первым. Дайте определение объединения более чем двух множеств.

2. Докажите, что 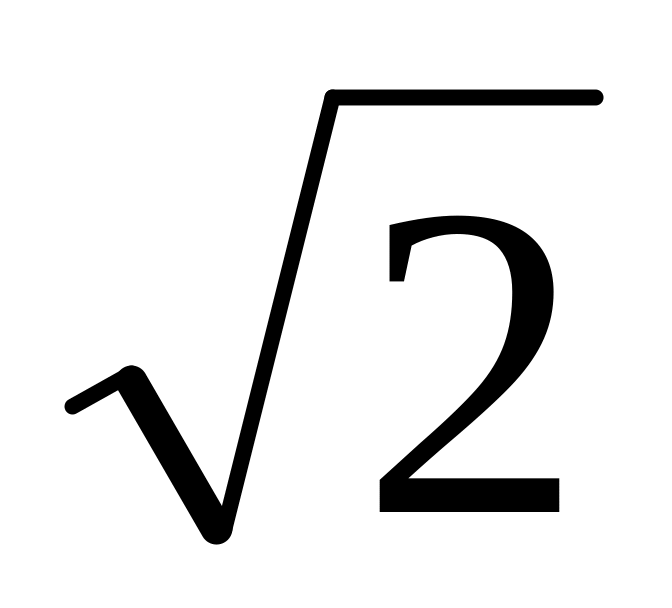не является рациональным числом.

3. Построить реберный граф для заданного на рисунке графа.

4. Теоретический вопрос: Парадокс Рассела.

Вариант № 9

1. Мы формируем объединение двух множеств, одно содержит 5 элементов, второе – 9 элементов. Какие из следующих чисел могут быть кардинальными числами нового объединенного множества: 4, 6, 9, 10, 14, 20? Объясните почему.

2. Докажите тождество: 1+3+…+ (2n–3) + (2n–1) = .

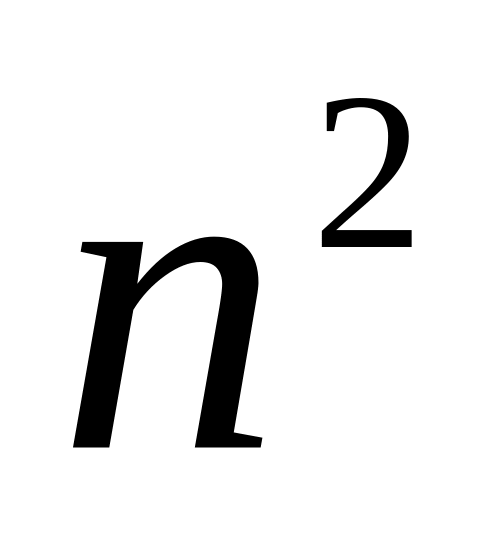3. Записать код Прюфера для дерева.

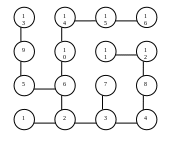
4. Теоретический вопрос: Сравнение множеств.

Вариант № 10

1. Мы формируем объединение двух множеств. Одно содержит n элементов, второе – m элементов. Какие предположения мы можем сделать о кардинальном числе нового объединенного множества?

2. Используя для размещений без повторений обозначение 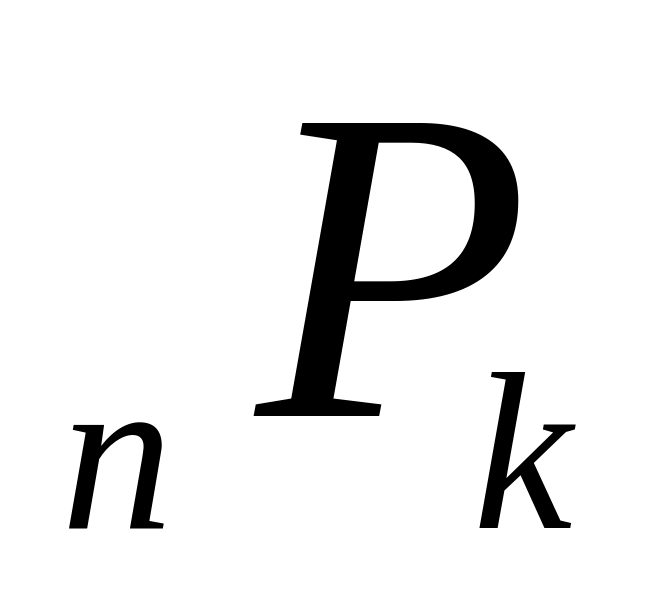, доказать формулу: .

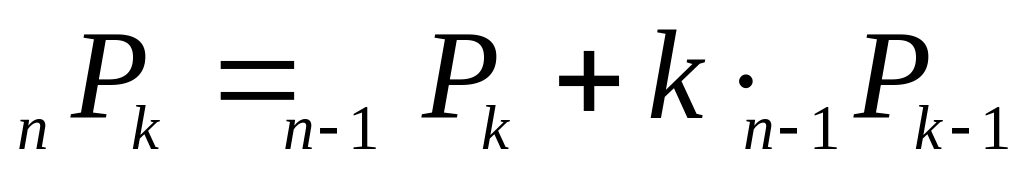3. Построить дерево, соответствующее коду Прюфера P=[5, 6, 7, 8, 6, 10, 14, 15, 11, 10, 6, 7, 8, 12].

4. Теоретический вопрос: Операции над множествами.

Вариант № 11

1. Найдите пересечение двух множеств 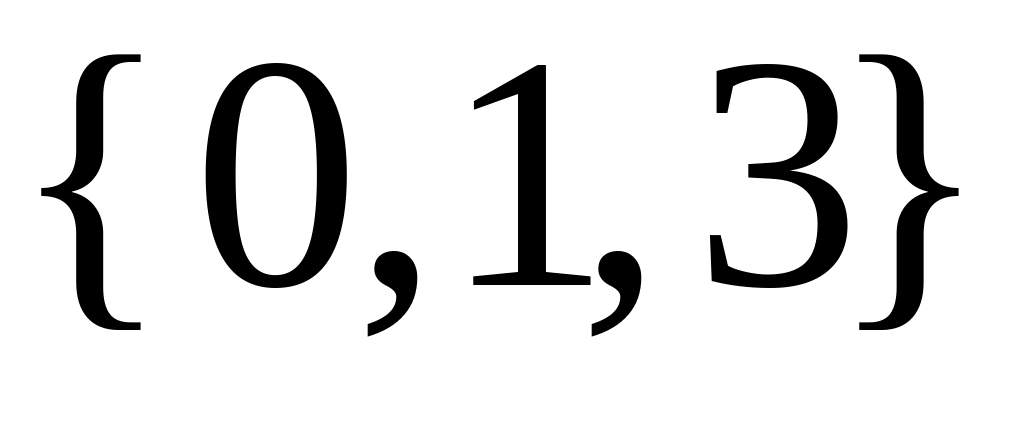и .

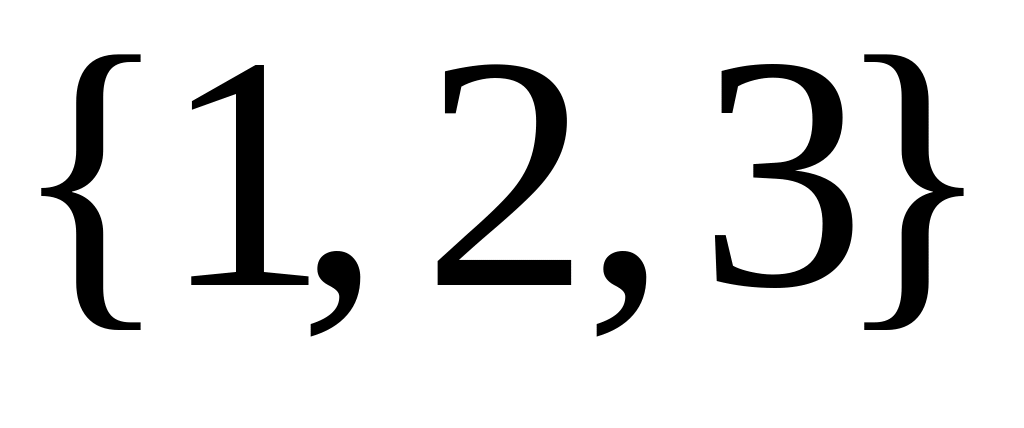2. Найти решение рекуррентного уравнения с начальным условием .

3. Дан взвешенный орграф. Найти кратчайший путь из вершины A в B.

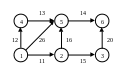
4. Теоретический вопрос: Булеан.

Вариант № 12

1. Мы формируем пересечение двух множеств. Одно из них содержит n элементов, второе – m элементов. Какие предположения мы можем сделать о кардинальном числе нового множества?

2. Найти решение неоднородного рекуррентного уравнения с начальными условиями .

3. Дан взвешенный граф. Найти число остовов графа минимального веса (экстремальное дерево).

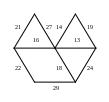
4. Теоретический вопрос: Виды математического доказательства.

ВАРИАНТ № 13

1. Докажите, что .

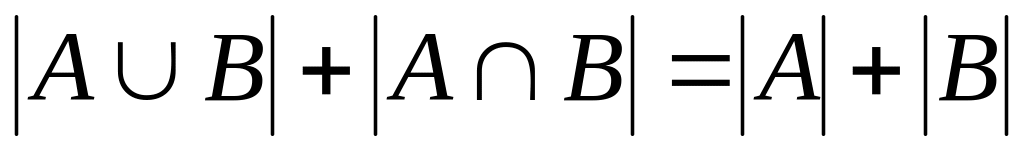2. Используя метод операционного исчисления, решить следующее дифференциальное уравнение: 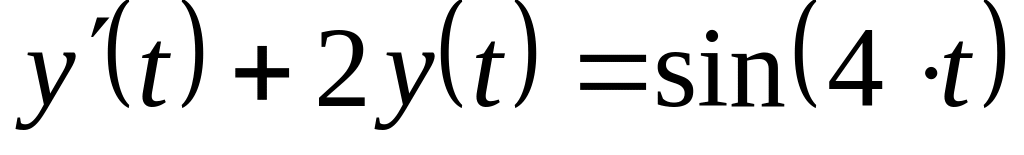с нулевым начальным условием .

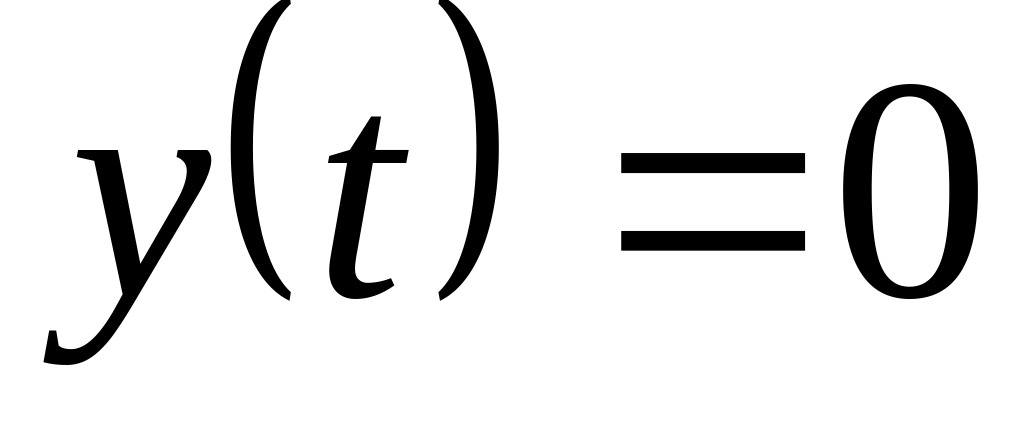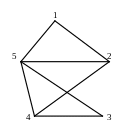
3. Найти радиус, диаметр и центр приведенного на рисунке графа. Проверить наличие эйлеровой цепи.

4. Теоретический вопрос: Принцип математической индукции.

ВАРИАНТ № 14

1. Какое число подмножеств имеет множество, содержащее n элементов и обязательно включающее некий выбранный элемент?

2. Получить решение следующего разностного уравнения с использованием -преобразования:

где

Причем, .

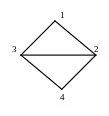
3. Найти хроматический полином показанного на рисунке графа.

4. Теоретический вопрос: Биномиальные коэффициенты.

ВАРИАНТ № 15

1. Сколько бит необходимо, чтобы записать число в двоичной форме?

2. Решить обыкновенное дифференциальное уравнение

,

при нулевых начальных условиях и .

3. Найти матрицу смежности и матрицу инцидентности приведенного на рисунке графа.

4. Теоретический вопрос: Треугольник Паскаля.

ВАРИАНТ № 16