Министерство образования и науки Украины
Восточноукраинский национальный университет им. Владимира Даля
Факультет компьютерных наук
Кафедра компьютерных наук
Методические указания
для выполнения контрольной работы
по дисциплине
«Основы дискретной математики»
для студентов заочной формы обучения
Составил доц. Погорелов О. А.
УТВЕРЖДЕНО
на заседании кафедры КН
протокол № 14
от 10 декабря 2008 года
Луганск 2008
Введение
Студент-заочник выбирает вариант задачи в соответствии со своим номером по списку в журнале группы.
В начале работы необходимо записать содержание задания. В конце работы необходимо привести список использованной литературы.
Ответы на вопросы должны быть даны в развернутой форме, с пояснениями, обоснованиями и доказательствами.
Контрольные работы должны быть выполнены согласно правилам оформления учебной документации. Необходимо использовать листы со штампом. Первый лист контрольной работы – с большим штампом, остальные – с маленькими.
К контрольной работе, распечатанной на листах, должен прилагаться электронный вариант на дискете (или на диске), сохранённый в формате Microsoft Word.
ВАРИАНТ № 1
Существует ли множество всех множеств?
Докажите следующую формулу:
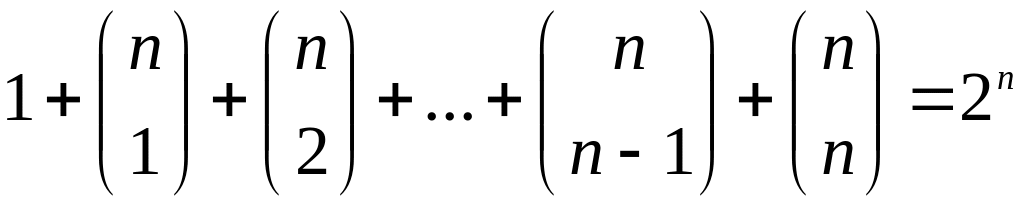.Найти радиус, диаметр и центр приведенного на рисунке графа. Проверить наличие эйлеровой цепи.
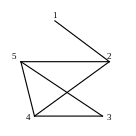
Теоретический вопрос: Счетные и несчетные числовые множества.
ВАРИАНТ № 2
Доказать, что
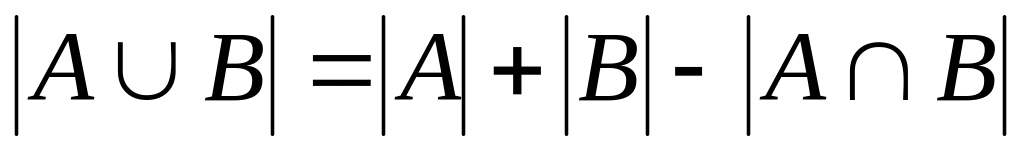.Найти решение неоднородного рекуррентного уравнения
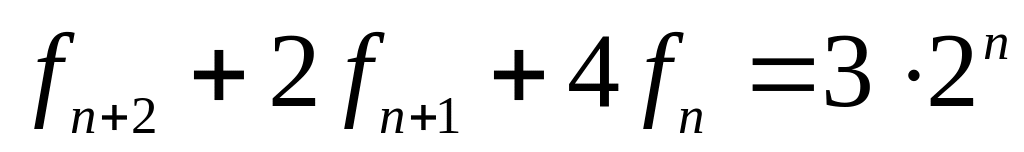с начальными условиями
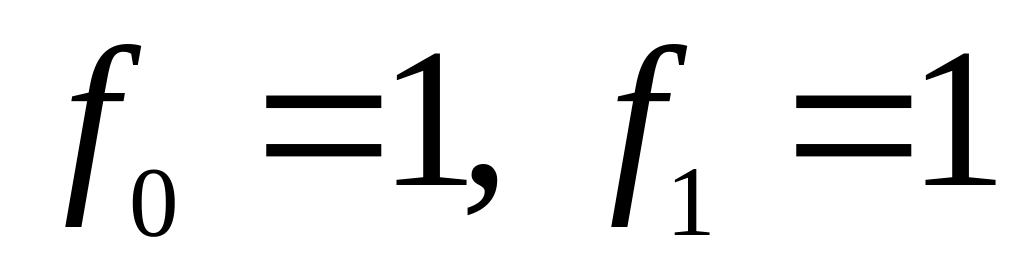.Найти хроматический полином показанного на рисунке графа.
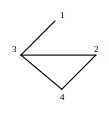
Теоретический вопрос: Рациональные и иррациональные числа.
ВАРИАНТ № 3
Доказать, что .
Докажите тождество:
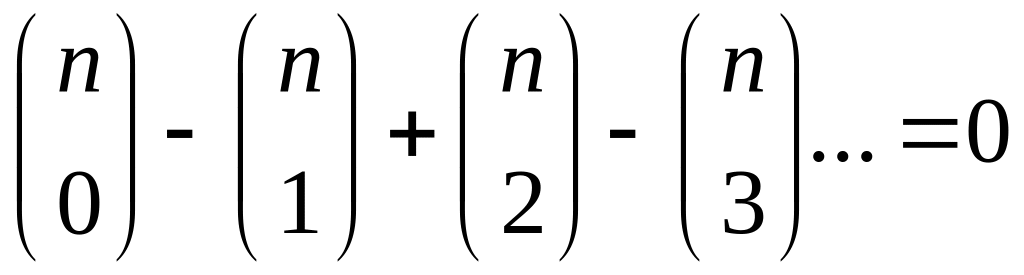.Найти ранг-полином графа.
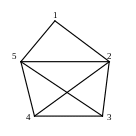
Теоретический вопрос: Логические высказывания, связки и операции.
ВАРИАНТ № 4
Заданы: пустое множество
,
множество натуральных чисел N,
множество целых неотрицательны чисел
,
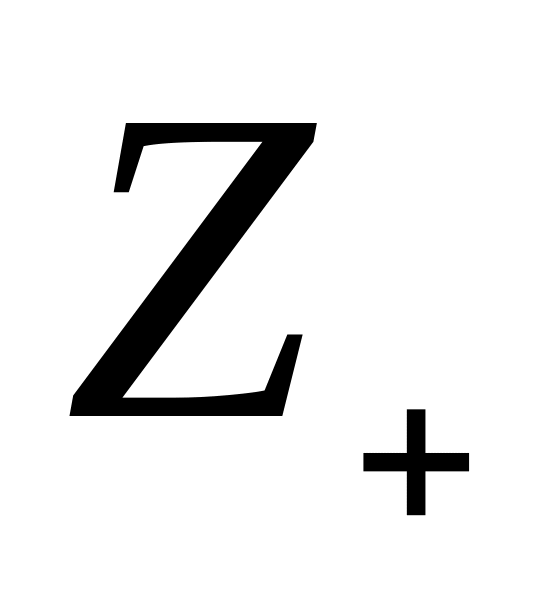множество целых чисел Z,
множество рациональных чисел Q
и множество действительных чисел R.
Мы можем записать различные отношения
между этими числовыми множествами.
Например, отношение
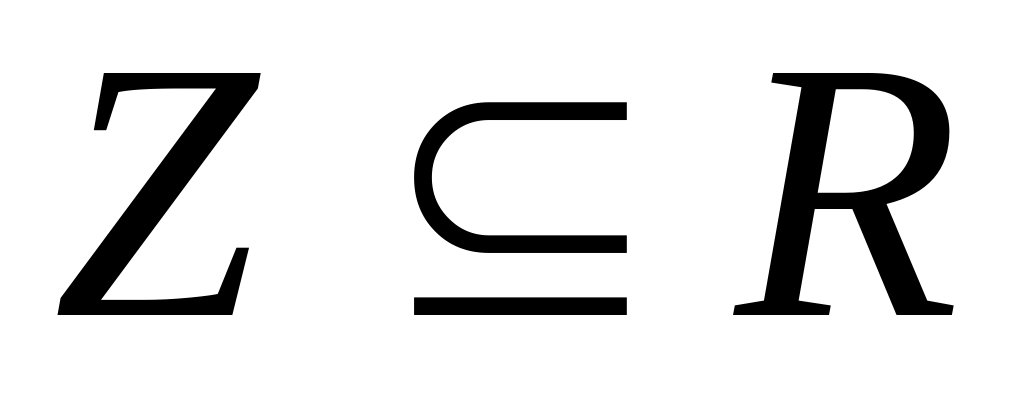является истинным. Сколько таких
истинных отношений можно отыскать
между множествами:
,
N,
,
Z,
Q,
R
?Докажите тождество для чисел Фибоначчи:
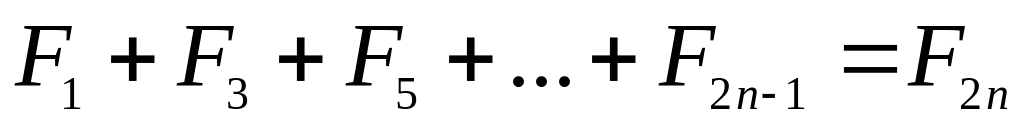.По заданной матрице смежности определить число циклов длины 3 и длины 4. Записать матрицу инцидентности и матрицу фундаментальных циклов.
Теоретический вопрос: Пропозициональные переменные и формулы.
ВАРИАНТ № 5
Запишите все подмножества множества
.
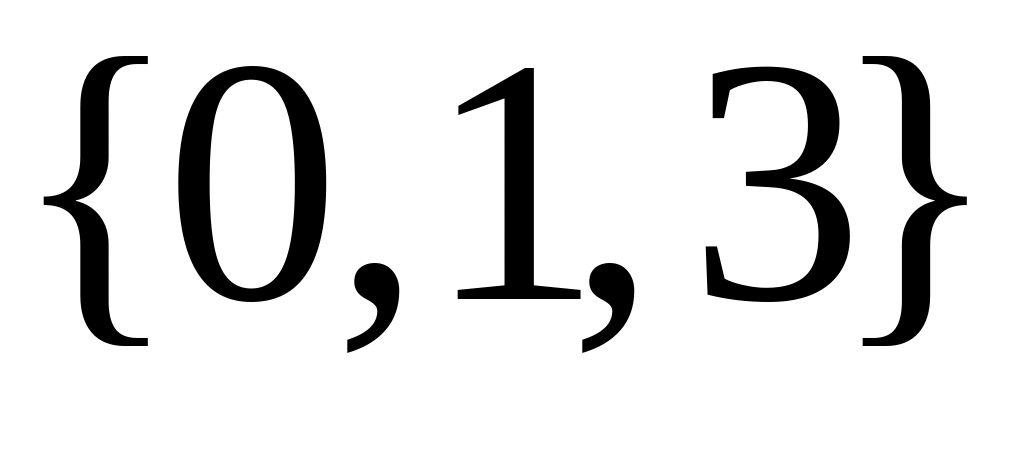Сколько их всего?Докажите тождество для чисел Фибоначчи:
.
На рисунке приведен орграф. Сколько в нем маршрутов длиной 3?
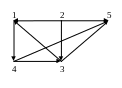
Теоретический вопрос: Булевы функции.
ВАРИАНТ № 6
Запишите все подмножества множества
,
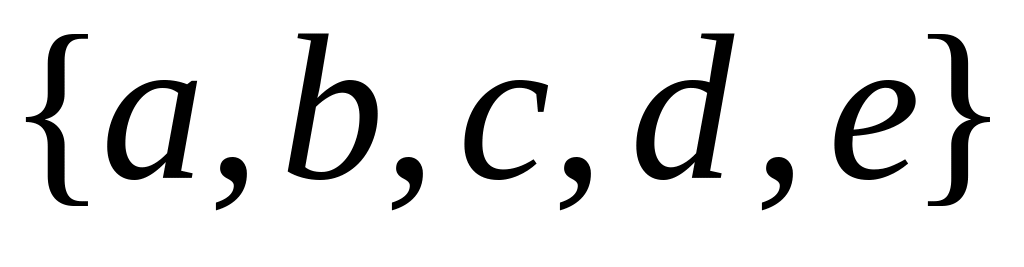содержащие
,
но не содержащие
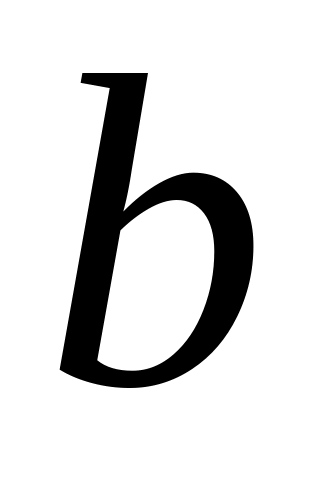.Найти решение рекуррентного уравнения
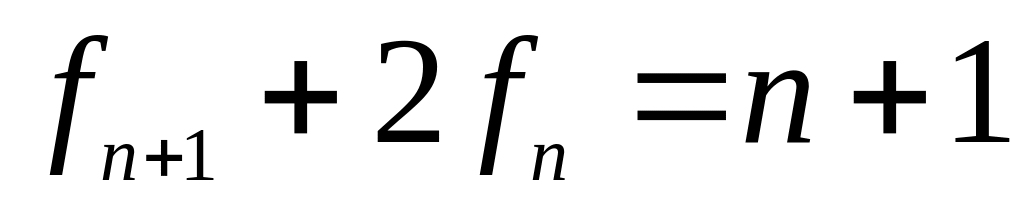с начальным условием
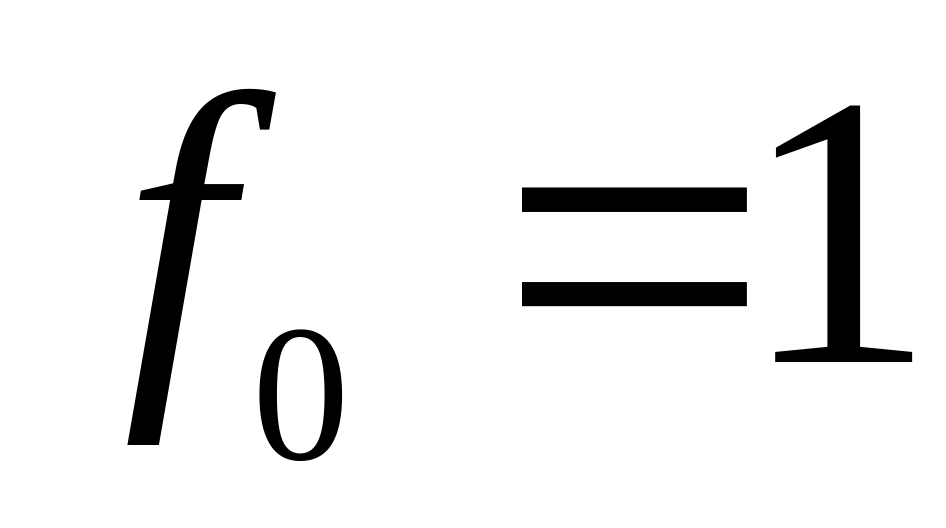.Найти компоненты сильной связности графа.
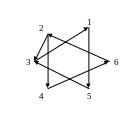
Теоретический вопрос: Предикаты.
ВАРИАНТ № 7