Лекція № 13. Орієнтовані графи

1. Основні визначення

Ребро в графі G може бути орієнтованим і мати почало|розпочало,зачало| і кінець. Таке ребро називається дугою, а граф, що містить|утримує| дуги, називається орієнтованим, або орграфом|. На малюнку дуга зображається|змальовується| стрілкою.

Багато понять, введених|запроваджених| для неографов|, для орграфов| набувають|придбавають| іншого визначення. Матриця відстаней для орграфа| несиметрична, і ексцентриситет вершини залежить від того, як вибирається максимум. Якщо максимум шукається в рядку, то ексцентриситет вершини називається числом зовнішнього розділення|поділу|, а якщо в стовпці – числом внутрішнього розділення|поділу|. Відповідно визначаються зовнішній і внутрішній центри.

Підстава|основа,заснування| орграфа| – неограф| з|із| тими ж вершинами, але|та| ребрами замість відповідних дуг.

Маршрут в орграфе| – послідовність вершин, сполучених|з'єднаних| дугами, направленими|спрямованими| в один бік.

Маршрут, в якому всі дуги різні, є шлях|колія,дорога|.

Шлях|колія,дорога|, в якому почало|розпочало,зачало| і кінець співпадають|збігаються|, є контур. Довжина шляху|колії,дороги| вимірюється числом вхідних в нього дуг, а для зваженого орграфа| – це сума ваги дуг.

У орграфе| два локальні ступені|міри| вершини v: – число дуг, що входять в v, і – число дуг, що виходять з|із| v. Лема про рукостискання для орграфа| має вигляд|вид|

, (13.1)

де підсумовування проводиться|виробляється,справляється| по всіх вершинах графа.

Множина вершин v, утворюючих дугу [v, u] з|із| вершиною u, називається множиною попередників вершини u, а множина вершин u, утворюючих дугу [v, u] з|із| вершиною v, називається множиною наступників|спадкоємців| вершини v. Потужності цих множин|безлічі| відповідно рівні: , .

Надалі під графом розумітимемо як неограф|, так і орграф|.

2. Маршрути в орграфе|

Завдання|задачі|, пов'язані з маршрутами в орграфе|, мають велике практичне значення, що і дає стимул до розвитку і вдосконалення методів їх рішення|розв'язання,вирішення,розв'язування|. Найчастіше встає питання про мінімальні і максимальні відстані, про число маршрутів певної довжини.

Приклад|зразок| 13.1. Заданий орграф| (мал. 13.1). Скільки в ньому маршрутів завдовжки 3?

Мал. 13.1

Рішення|розв'язання,вирішення,розв'язування|. Використовуємо алгебраїчний метод рішення задачі, на підставі теореми 12.4. Запишемо матрицю суміжності. Матриця суміжності орграфа| – несиметрична.

, .

Піднесемо цю матрицю до ступеня 3. Підсумовуючи всі елементи одержаної|отриманої| матриці, знаходимо|находимо|, що число маршрутів завдовжки 3 рівне восьми. Три одиниці, що стоять по діагоналі, показують, що сюди входить 3 помічених|позначених| контури. Очевидно, що це контури: 1–4–3, 4–3–1, 3–1–4.

3. Транзитивне замикання

Прямою (декартовою) добичею|добутком| множин A і B називається множина|безліч| . Бінарне відношення|ставлення| на X – будь-яка підмножина прямої добичі|добутку|: .

Відношення|ставлення| на X рефлексивно, якщо для будь-якої пара .

Відношення|ставлення| на X антирефлексивно, якщо для будь-якої пара .

Відношення|ставлення| на X симетрично, якщо для будь-якої пари з|із| умови виходить .

Відношення|ставлення| на X антисиметрично, якщо з|із| умов і слідує|прямує| x = у|в,біля|.

Відношення|ставлення| на X асиметрично, якщо для будь-якої пари з|із| умови виходить .

Відношення|ставлення| на X транзитивно, якщо для будь-яких двох пар і з|із| умов і слідує|прямує| .

Відношення|ставлення| називається замиканням відношення|ставлення| на властивість A, якщо володіє властивістю A, і для будь-якого відношення|ставлення| з|із| властивістю A справедливо вкладення .

Композицією бінарних відносин і називають відношення|ставлення|, що складається з пар , таких, що і .

Транзитивне замикання відношення|ставлення| має вигляд |вид|, де , .

Теорема 13.1. Відношення|ставлення| транзитивно тоді і тільки|лише| тоді, коли .

Граф є відношення|ставлення| на безлічі вершин. Елементами цього відношення|ставлення| є|з'являються,являються| дуги (або ребра, якщо відношення|ставлення| симетрично).

Орграф називається транзитивним, якщо для будь-яких його дуг і існує замикаюча дуга .

Приклад|зразок| 13.2. Дане відношення|ставлення|, задане матрицею

.

Досліджувати відношення|ставлення| на симетрію, антисиметрію, асиметрію, рефлексивність, антирефлексивність. Знайти транзитивне замикання відношення|ставлення|. Побудувати|спорудити| граф відношення|ставлення| і його транзитивного замикання.

Рішення|розв'язання,вирішення,розв'язування|.

1. Дане відношення|ставлення| не є|з'являється,являється| симетричним, оскільки|тому що| матриця несиметрична. Наприклад, пара (2, 1) належить , а пара (1, 2) йому не належить.

2. Відношення|ставлення| антисиметрично, оскільки|тому що| немає жодної пари , .

3. Відношення|ставлення| антисиметрично, але|та| не асиметрично, оскільки|тому що| на діагоналі матриці є|наявний| елементи, рівні 1.

4. Всі діагональні елементи матриці відношення|ставлення|, рефлексії, рівні 1. Дане відношення|ставлення| не є|з'являється,являється| рефлексією.

5. Відношення|ставлення| не володіє властивістю антирефлексивності, оскільки|тому що| діагональ матриці ненульова.

6. Дане відношення|ставлення| не є|з'являється,являється| транзитивним, оскільки|тому що|, наприклад, пари (1, 4) і (4, 3) належать , а пара (1, 3) йому не належить.

Знайдемо транзитивне замикання графа, заданого відношенням|ставленням| . Процедура транзитивного замикання зводиться до додавання|добавки| в матрицю суміжності мінімального числа одиниць, так, щоб відповідне відношення|ставлення| володіло властивістю транзитивності. Для цього виконуємо наступні|такі| операції.

1. Обчислюємо|обчисляємо,вичисляємо| матрицю композиції . Для цього умножаємо|множимо| (з використанням операції логічного множення) матрицю A саму на себе: . Така добич|добуток| називається добичею|добутком| булевих матриць. Результат добичі|добутку| одержують|отримують| таким чином. Елемент результуючої матриці, якщо хоч би в одному випадку k-й| елемент i-й рядки першого співмножника і k-й| елемент j-го стовпця другого співмножника одночасно рівні одиниці. Інакше .

.

2. Знаходимо|находимо| логічну суму (диз'юнкцію) матриць. Поелементна диз'юнкція матриць дає:

.

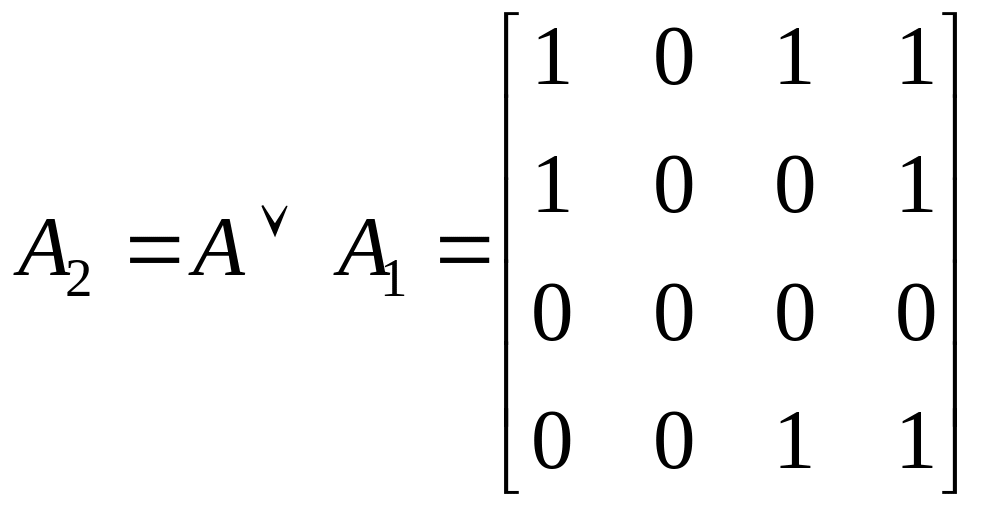3. Порівнюємо з|із| A. Якщо = A, то – шукана матриця. Якщо 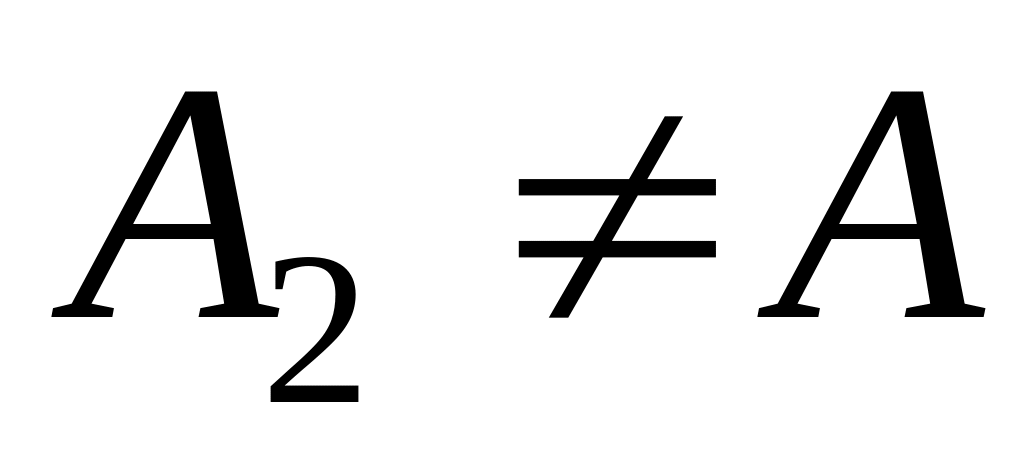, то вважаємо |гадаємо|, повертаємося до п. 1 і повторюємо всю процедуру для нової матриці. В даному випадку . Тому приймаємо:

.

Умножаємо|множимо| матрицю саму на себе:

.

Знаходимо|находимо| логічну суму:

.

Порівнюємо: . Вважаємо|гадаємо| і повторюємо процедуру ще раз.

.

.

Порівнюємо: . Отже, – матриця транзитивного замикання заданого відношення|ставлення|.

На мал. 13.2 (а і б) представлені|уявлені| графи відношення|ставлення| і його транзитивного замикання. Діагональні елементи матриці відповідають петлям на графі. Матриця несиметрична, тому граф відношення|ставлення| – орієнтований.

Мал. 13.2