13. (Химические реакторы) п-рис-н. Математическое описание.
В политропическом реакторе имеет место теплообмен и температура реакционной массы меняется, причем изменение температуры может происходить по любому закону, независимо от величины теплового эффекта протекающей в нем реакции и степени превращения, поэтому задача расчета политропического реактора заключается в определении оптимального профиля температуры при которой скорость процесса в любой момент времени была бы максимальна.
Исходным уравнением для расчета реакторов
служит дифференциальное уравнение
конвективного теплообмена:
.
Для РИС-Н уравнение теплового баланса выглядит так:
,
где
- выражает скорость накопления тепла,
в любой точке для которой составляется
баланс;
- отражает изменение тепла связанное с
движением реакционной смеси;
- изменение тепла связанное с теплоотдачей
в окружающую среду;
- изменение тепла связанное с химическим
превращением.
Из выше указанного следует:
;
,
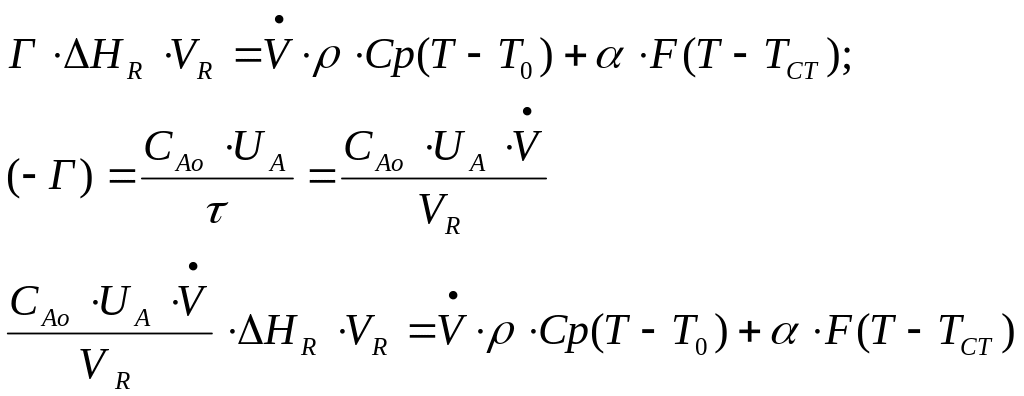где
после всех сокращений получаем:
;
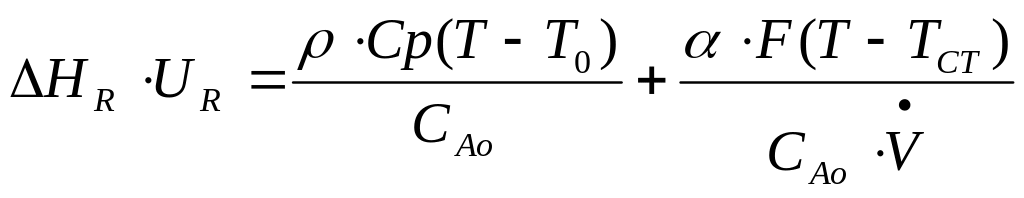заменяем
,
- мольный расход компонента А, в начальный
момент времени; отсюда следует:
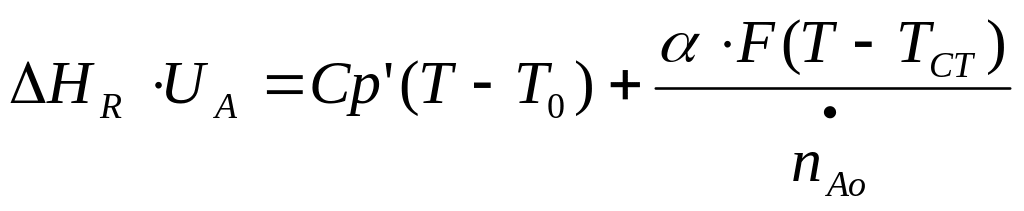- математическое описание П-РИС-Н.
14. (Химические реакторы) п-рив-н. Математическое описание.
В политропическом реакторе имеет место теплообмен и температура реакционной массы меняется, причем изменение температуры может происходить по любому закону, независимо от величины теплового эффекта протекающей в нем реакции и степени превращения, поэтому задача расчета политропического реактора заключается в определении оптимального профиля температуры при которой скорость процесса в любой момент времени была бы максимальна.
Исходным уравнением для расчета реакторов служит дифференциальное уравнение конвективного теплообмена: .
Для РИВ-Н:
,
,
;
следовательно:
- ур-ние теплового баланса для РИВ-Н.
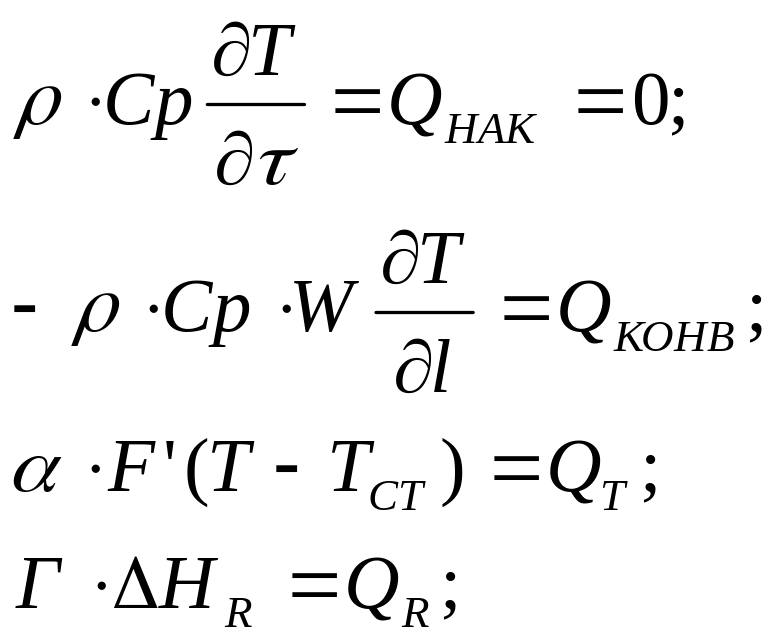
следовательно:
;
соответственно:
,
отсюда следует:
;
произведем сокращение в выше указанном уравнении и получим:
;
произведем некоторую замену:
;
;
;
;
пусть
,
тогда
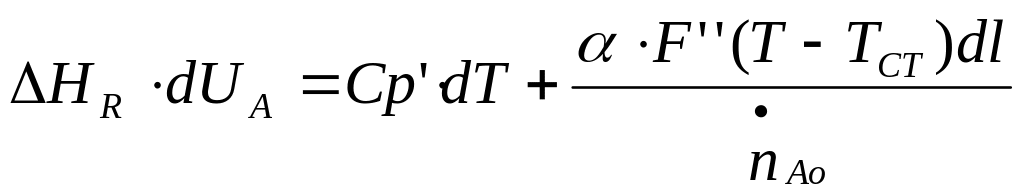- математическое описание П-РИВ-Н.