1. (Хим. Реакторы) рис-п. Характеристическое уравнение.
Одним из важнейших показателей, отражающих совершенство хим. реактора, является его интенсивность. Она характеризуется количеством целевого продукта получаемого в единицу времени при заданных условиях с единицы объема или площади аппарата. Интенсивность реактора тем выше, чем меньше времени затрачивают на получение целевого количества продукта. Главной задачей при изучении процессов протекающих в реакторах любого типа является установление функциональной зависимости времени пребывания реактанта в реакторе.
-характеристическое
уравнение реактора.
Его составляют по одному из компонентов рассматриваемой реакции.
Составим ур-е для
(простая необратимая реакция). Исходным
ур-ем для получения характеристического
ур-я служит дифференциальное ур-е
конвективного массообмена, в которое
вводят дополнительный член, учитывающий
изменение концентрации компонента в
следствии хим. реакции.
; где
-концентрация
А в исходной смеси
-скорости
потоков по координатам x,y,z
-коэф.
молекулярной диффузии
-скорость
реакции
РИС-П
Поскольку все параметры одинаковые по
всему объему реактора, следовательно:
;
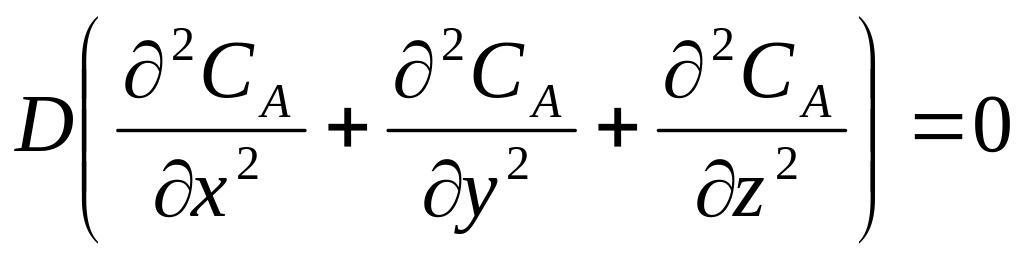
где
,
(для V=const)
или
подставляя и преобразовывая, получаем:
;
и получаем:
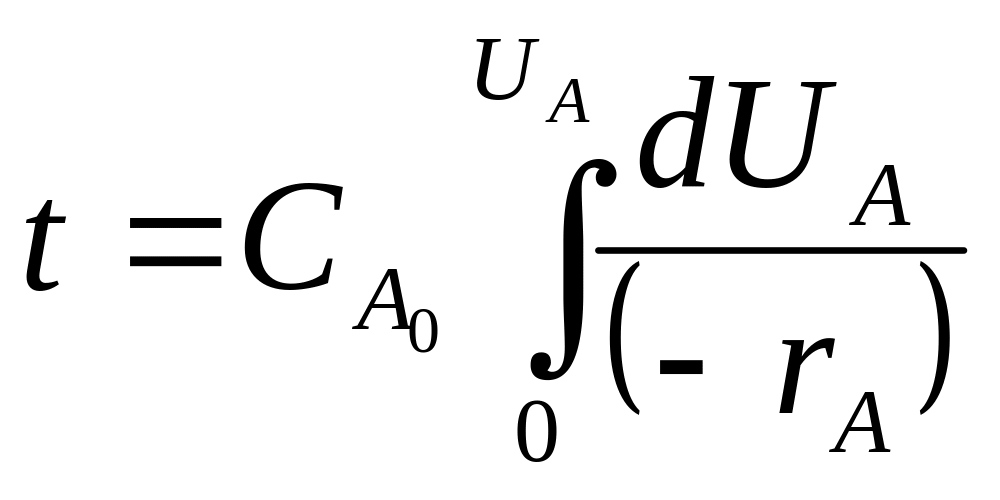- характеристическое ур-е РИС-П
Реакция n-го порядка:
подставим в хар-е ур-е:
;
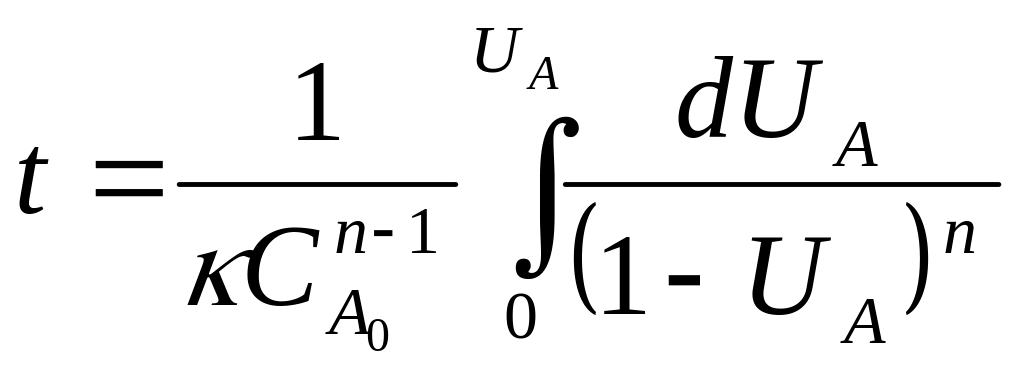(V=const)
Реакция 0-го порядка:
,
тогда:
;
(V=const)
Реакция 1-го порядка:
,
тогда:
;
(V=const)
Если V изменяется в течение
процесса, то это изменение учитывают
при помощи коэф. относительного изменения
объема (при
)
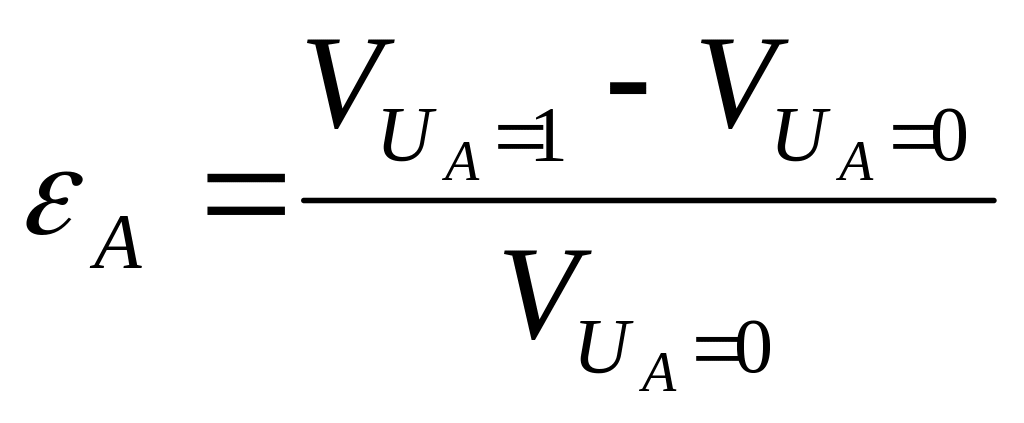
Для случая линейного изменения объема:
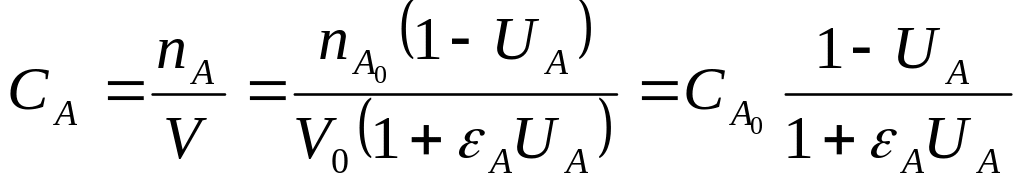
Получим хар-е ур-е для случая линейного изменения объема:
;
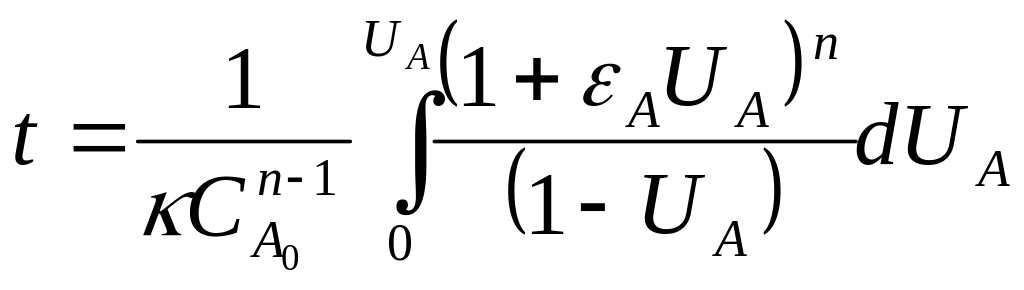(для n-го порядка
2. (Хим. Реакторы) рив-н. Характеристическое уравнение.
Одним из важнейших показателей, отражающих совершенство хим. реактора, является его интенсивность. Она характеризуется количеством целевого продукта получаемого в единицу времени при заданных условиях с единицы объема или площади аппарата. Интенсивность реактора тем выше, чем меньше времени затрачивают на получение целевого количества продукта. Главной задачей при изучении процессов протекающих в реакторах любого типа является установление функциональной зависимости времени пребывания реактанта в реакторе.
-характеристическое уравнение реактора.
Его составляют по одному из компонентов рассматриваемой реакции.
Составим ур-е для (простая необратимая реакция). Исходным ур-ем для получения характеристического ур-я служит дифференциальное ур-е конвективного массообмена, в которое вводят дополнительный член, учитывающий изменение концентрации компонента в следствии хим. реакции. ; где
-концентрация А в исходной смеси
-скорости потоков по координатам x,y,z
-коэф. молекулярной диффузии
-скорость реакции
РИВ-Н
Если в периодическом реакторе можно
непосредственно измерить продолжительность
реакции, то в реакторах непрерывного
действия этого сделать невозможно, т.к.
в реакторах при установившемся режиме
параметры со временем не меняются.
Поэтому для непрерывных реакторов
пользуются условным временем пребывания
компонентов системы в реакторе:
(
-объем
реактора;
-объемный
расход).
Тогда дифференциальное ур-е конвективного массообмена примет вид:
(W-линейная
скорость движения смеси в реакторе;
L-длина пути пройденного
элементом объема смеси в реакторе)
;
-уравнение
мат. баланса при нестационарном режиме.
-стационарный
режим, тогда:
(V=const)
;
;
подставляя и преобразовывая, получаем:
;
и получаем: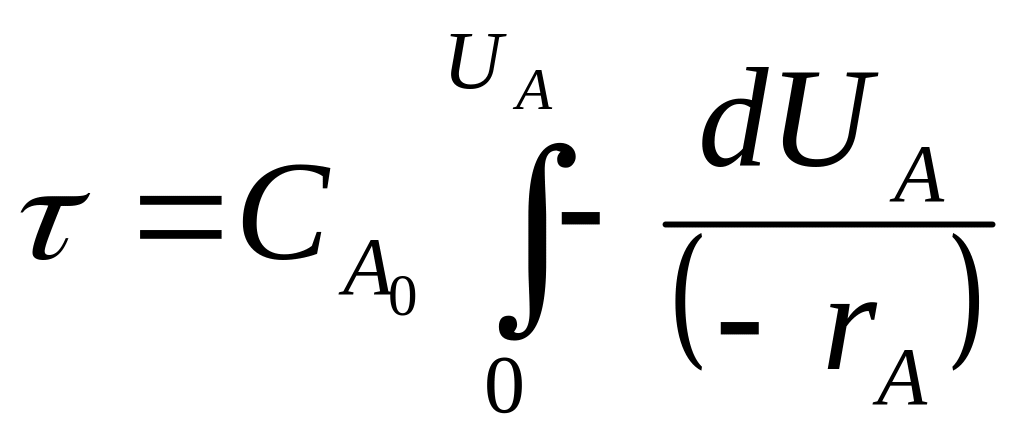
- характеристическое ур-е РИВ-Н (V=const)