48. Алгебраическая форма

Запись комплексного числа   в виде  ,  , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что  ):

Тригонометрическая и показательная формы

Если вещественную   и мнимую   части комплексного числа выразить через модуль   и аргумент   ( ,  ), то всякое комплексное число  , кроме нуля, можно записать в тригонометрической форме

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:

где   — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

49.Свойства комплексных чисел:

Свойства комплексных чисел:

1) комплексные числа коммутативны по сложению и по умножению.

2) комплексные числа ассоциативны по сложению и по умножению.

3) комплексные числа дистрибутивны.

Для комплексных чисел операция деления определена как операция обратная операции умножения. Если  , то z является решением уравнения  . Решим это уравнение, домножив левую и правую часть на   и разделив обе части на квадрат модуля. Получим, что

50. Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i(здесь как раз используется, что i² = –1). Число   = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z ·   = a² + b² позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:

.

(Например,  .)

У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна  . Эта величина называется модулем комплексного числа z = a + biи обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументомкомплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор.

51. Формула Муавра для комплексных чисел   утверждает, что

для любого 

Доказательство.

Формула Муавра сразу следует из формулы Эйлера   и тождества для экспонент  , где b — целое число.^[1]

Применение

Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа:

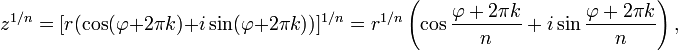
где k = 0, 1, …, n—1.

Из основной теоремы алгебры следует, что корни n-й степени из комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n-угольника, вписанного в окружность радиуса   с центром в нуле.

1. Если b — нецелое число, то 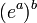  — многозначная функция переменной a и   является лишь одним из её значений.

51. формула Муавра: zⁿ = |z|ⁿ · (cos(n · (Arg z)) + i sin(n · (Arg z))). С помощью этих формул легко научиться извлекать корни любой степени   из комплексных чисел. Корень n-й степени из числа z — это такое комплексное число w, что wⁿ = z. Видно, что  , а  , где kможет принимать любое значение из множества {0, 1, ..., n – 1}. Это означает, что всегда есть ровно n корнейn-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).