59. Теорема об изменении кинетической энергии

и Работа силы. Элементарная работа силы равна скалярному произведению силы на дифференциал радиус-вектора точки приложения силы.

Элементарная работа силы равна также скалярному произведению элементарного импульса силы на скорость точки.

Если сила F перпендикулярна приращению радиус-вектора dr, то элементарная работа силы равна нулю.

Полная работа сил

Другое определение: , где t=0 соответствует положению М₀, а момент времени t – положению М.Последняя формула удобна для вычисления работы силы, когда сила известна как функция времени.Размерность работы [A]=1Дж=1Нм

Мощность. Мощность силы или работоспособность какого-либо источника силы часто оценивают той работой, которую он может совершить за единицу времени. Размерность мощности [W]=1Вт=1Дж/с.Работсилтяжести. P_x=0, P_y=0, P_z= - mg Для системы точек для каждой точки работа A_i=m_ig(z_0i-z_1i), полная работа

:

60. При движении тел в жидкости, сила трения пропорциональна первой степени скорости.

При поступательном движении тела все его точки движутся также как и и его центр масс. Поэтому дифференциальные уравнения движения центра масс тела являются дифференциальными уравнениями поступательного движения твёрдого тела:  с y и z такие же уравнения m- масса тела,  - координаты центра масс тела  - проекция внешней силы F на оси координат X,Y,Z – проекции главного вектора внешних сил R на эти оси. По дифференциальным уравнениям поступательного движения можно решать два основных типа задач на поступательное движение твёрдого тела: 1) по заданному движению твёрдого тела определить главный вектор, приложенных к нему сил 2) по заданным внешним силам, действующим на тело, и начальным условиям движения находить кинематические уравнения движения тела, если известно, что оно движется поступательно.Уравнение  представляет собой дифференциальное уравнение вращения твёрдого тела вокруг неподвижной оси. По дифференциальному уравнению можно решать следующие задачи: 1) по заданному уравнению вращения тела  и его моменту инерции  определять главный момент внешних сил, действующих на тело :  2) по заданным внешним силам, приложенным к телу, по начальным условиям вращения  и по моменту инерции  находить уравнение вращения тела  3)определять момент инерции тела  относительно оси вращения, зная величины  и

61. Уравнение движения материальной точки массой т относительно инерциальной системы отсчета под действием приложенных сил, равнодействующая которых , имеет вид Перепишем это уравнение в виде Введя обозначение получим Вектор , равный по модулю произведению массы точки на ее ускорение и направленный противоположно вектору ее ускорения, называется силой инерции.Уравнение (6.4) выражает принцип (уравнение) Д'Аламбера: в каждый момент движения геометрическая сумма внешних сил и силы инерции равна нулю.При этом следует иметь в виду, что к материальной точке приложена только равнодействующая сила т.е. внешняя сила и реакция связи, если точка не свободна. Сила же инерции к точке не приложена, а появляется при движении точки.

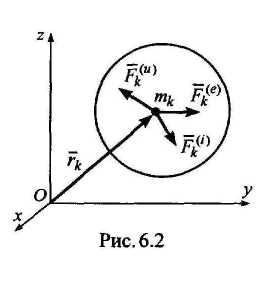
Метод кинетостатики является формальным приемом сведения уравнения динамики к уравнениям статики, причем при решении практических задач такой прием обладает рядом достоинств.Рассмотрим материальную точку массой т_k системы, состоящей из N точек (рис. 6.2). Обозначим ускорение этой точки a_k, равнодействующую внешних сил через , равнодействующую внутренних сил, приложенных к той же точке через . Реакции связей входят в . Тогда принцип (6.4) будет иметь вид ,(6.4)где .Складывая почленно все N уравнений получим k = l,2,...,N.(6.6)Первая сумма в уравнении (6.6) равна главному вектору внешних сил, приложенных к системе; вторая сумма равна нулю, поскольку геометрическая сумма всех внутренних сил системы равна нулю; последняя - главному вектору сил инерции. Таким образом, (6.6) запишем как , т.е. в каждый момент времени сумма главных векторов внешних сил и сил инерции движущейся системы равна нулю.Выберем произвольный полюс О и проведем из него к точке т_к радиус-вектор (рис. 6.2). Умножая каждое слагаемое из (6.6) векторно на соответствующий радиус-вектор слева и складывая все N полученных таким образом уравнений, име k = l,2,...,N Первая сумма равна главному моменту внешних сил, приложенных к системе; вторая сумма равна нулю,последняя -главному моменту сил инерции. Следовательно, , т.е. в каждый момент времени сумма главных моментов внешних сил и сип инерции движущейся механической системы равна нулю.

Двум векторным уравнениям (6.7) и (6.8) соответствуют шесть уравнений в проекциях на оси декартовых координат Движение твердого тела, как частный случай механической системы, вполне определяется этими шестью уравнениями. Если рассматривается система, состоящая из нескольких тел, то можно составить соответствующие уравнения для каждого тела в отдельности.

62. Вычислим главный вектор сил инерции. Имеем Сумма , где r_c - радиус-вектор центра масс системы, следовательно, т.е. главный вектор сил инерции системы равен произведению массы всей системы на ускорение центра масс, приложен в точку центра масс и направлен противоположно вектору а_с.6.2.2. Главный вектор сил инерции твердого тела

Твердое тело является частным случаем механической системы. Следовательно, главный вектор сил инерции твердого тела находится также по формуле (6.10).Тогда проекции главного вектора на декартовые оси координат имеют вид , (6.11)здесь х_с, y_c, z_c - координаты центра масс тела.

Если тело движется прямолинейно по си х, то 6.2.3.Главный момент сил инерции механической системыВычислим главный момент сил инерции системы. Имеем , k = 1,2,..,N; (6.12)так как , преобразуем правую часть

Здесь - кинетический момент системы.Подставляя (а) в (6.12), получаем значение главного момента сил инерции

63.Система материальных точек называется свободной, если положение отдельных её точек и их скорости могут принимать произвольное значение. Несвободной - если на положение и скорости точек системы наложены ограничения геометрического или кинематического характера, называемыми связями.

Связями называют любого вида ограничения, налагаемые на положения (координаты) и скорости точек механической системы.

Конструктивно связи осуществляются в виде нитей, стержней, шарниров, опор, поверхностей и т.д. Аналитически связи выражаются уравнениями или неравенствами, т.е. соотношениями между радиус - векторами точек системы, их скорости и времени. Связи можно разделить на два типа: удерживающие (двухсторонние) и неудерживающие (односторонние). Удерживающими связями называются связи, которые сохраняют свое действие во все время движения точек системы. Аналитически эти связи выражаются уравнениями, связывающие координаты точек, их скорости и времздесь - радиус вектор, определяющий положение k-той точки системы, - ее скорость, t - время.Примером удерживающей связи может служить система из двух материальных точек т₁ и т₂, которые соединены стержнем постоянной длины L. В этом случае уравнение связи имеет вид Неудерживающими связями называются связи, которые могут в некоторые промежутки времени меняться. Аналитически они выражаются неравенством, связывающим координаты точек системы, их скорости и время.Примером неудерживающей связи может служить система из двух материальных точек, которые соединены гибкой нитью длинной L. В этом случае уравнение связи имеет вид

В дальнейшем будем рассматривать только удерживающие связи.Связь называется стационарной, если она не меняется с течением времени. В уравнение стационарной связи не входит время t в явном виде.

П римером механизма, имеющего стационарные связи, может служить кривошипно-шатунный механизм (рис. 1). Механизм состоит из кривошипа ОА длинной r, шатуна АВ длинной L и ползуна В.Уравнения связи данного механизма запишутся: ,

Первое уравнение определяет постоянную длину кривошипа, второе - постоянную длину шатуна.

Связь называется нестационарной, если она меняется с течением времени. Уравнение такой связи содержит время t явно.Например, материальная точка может двигаться только по поверхности. Пусть уравнение поверхности задано в виде функции f(х,у,z) = 0. Это стационарная связь. Если поверхность подвижная или деформирующаяся, то в уравнение поверхности время г войдет явно: f(х,у,z,t) = 0. В этом случае связь нестационарная. Примером нестационарной связи является, также деформируемое твердое тело.Связь называется конечной или геометрической, если она накладывает ограничения только на координаты точек системы. Уравнение конечной (геометрической) связи имеет вид

Эта связь не налагает ограничение на скорости точек системы.

В общем случае удерживающая связь (1.1) называется кинематической или дифференциальной. Эта связь налагает ограничения на положение координат точек системы и на скорости этих точек.Если кинематическая (дифференциальная) связь интегрируется, то после интегрирования связь перестает быть таковой и становиться конечной (геометрической) связью. Следовательно, связь будет кинематической (дифференциальной) только в том случае, если она неинтегрируемая.

Система называется склерономной, если на нее наложены только стационарные связи. В противном случае система называется реономной.Голономной называется всякая свободная система материальных точек, а также несвободная система с конечными или дифференциальными, но интегрируемыми связями. При наличии дифференциальных неинтегрируемых связей, система называется неголономной.

Рассмотрим пример голономной связи. Колесо радиуса R катиться без скольжения по прямолинейному рельсу (рис. 2).Положение колеса в плоскости движения хОу определяется координатами центра колеса (полюса) х_с, у_с и углом поворота φ. Если

ось Ох направить вдоль рельса, то у_с = R, следовательно, наложено ограничение на координату у, связь - конечная (геометрическая).Кроме того, должна быть равна нулю скорость точки Р, точки касания колеса с рельсом. Это условие запишется в виде уравнения .. Последнее уравнение накладывает ограничения на скорости, поэтому связь будет дифференциальной (кинематической). Но это уравнение сразу интегрируется и приводит к соотношению между координатами х_с и φ, имеющему вид х_с=Rφ. Таким образом, рассмотренная система является голономной.В качестве примера неголономной связи рассмотрим движение конька по поверхности льда. При отсутствии скольжения вектор скорости центра тяжести конька С должен быть направлен по касательной к траектории движения - по оси т (рис. 3). Имеем: , где φ - угол, образованный осью х и касательной к траектории движения в точке С - осью . Разделив второе соотношение на первое, получим , откуда . Таким образом получено уравнение, накладывающее ограничения на скорость. Это уравнение не может быть проинтегрировано, поскольку угол φ - переменный (угол φ=φ(t) определяет направление оси , поэтому это уравнение является уравнением неголономной связи.

64.В аналитической механике эффект действия связи определяется возможными перемещениями точек.

Возможным перемещением точки называется такое бесконечно малое (элементарное) мысленное перемещение, которое допускается в рассматриваемый момент времени наложенными на точку связями.

Таким образом, возможные перемещения - это перемещения, допускаемые связями. Для каждого возможного положения системы в момент времени t существует бесчисленное множество возможных перемещений. Обозначать возможные перемещения будем символом δ.Действительным перемещением точки называется бесконечно малое перемещение под действием внешних сил в соответствии с законом движения и уравнением связи. Обозначать действительные перемещения будем символом d, например, на рис. 4.При действительном движении системы в момент времени t реализуется одно из возможных перемещений. Для груза, расположенного на наклонной плоскости (рис. 4), действительное и возможное перемещения совпадают, т.е. dS=δS.В общем случае система может иметь несколько или бесконечно много возможных перемещений. Вследствие уравнений связей, наложенных на систему, не все возможные перемещения являются независимыми.Число независимых возможных перемещений называют числом степеней свободы системы.

65. Положением равновесия называется такое положение системы, в котором система будет находиться все время, если в начальный момент времени она находилась в этом положении, и скорости всех ее точек были равны нулю.Положение системы будет положением равновесия в том случае, когда в этом положении системы выражает принцип возможных перемещенийдля того, чтобы стационарная механическая система с идеальными конечными связями находилась в положении равновесия, необходимо и достаточно, чтобы в этом положении сумма элементарных работ внешних сил на любых возможных перемещениях системы равнялась нулю.Принцип возможных перемещений был известен со времен Архимеда под названием «золотого правила механики» и применялся к простейшим механизмам. Рассмотрим в качестве примера рычаг Архимеда (рис. 12). Рычаг имеет одну степень свободы - может вращаться вокруг точки О. Равновесие имеет место, когда элементарная работа при повороте рычага на элементарный угол δφ равна нулю.

66. Неудерживающими связями называются связи, которые могут в некоторые промежутки времени меняться. Аналитически они выражаются неравенством, связывающим координаты точек системы, их скорости и время .Примером неудерживающей связи может служить система из двух материальных точек, которые соединены гибкой нитью длинной L. В этом случае уравнение связи имеет вид /

В дальнейшем будем рассматривать только удерживающие связи.Связь называется стационарной, если она не меняется с течением времени. В уравнение стационарной связи не входит время t в явном виде.

П римером механизма, имеющего стационарные связи, может служить кривошипно-шатунный механизм (рис. 1). Механизм состоит из кривошипа ОА длинной r, шатуна АВ длинной L и ползуна В.

Уравнения связи данного механизма запишутся: ,

Первое уравнение определяет постоянную длину кривошипа, второе - постоянную длину шатуна.

Связь называется нестационарной, если она меняется с течением времени. Уравнение такой связи содержит время t явно.

67. Общее уравнение динамики относится к уникальному методу исследования задач динамики механических систем.Рассмотрим голономную систему N материальных точек, подчиненную идеальным связям. Каждая точка системы движется согласно основному закону динамики где т_k - масса k-ой точки системы, - ее ускорение, - равнодействующая внешних сил, приложенных к k-ой точке (k = 1,2,...,N).

Если ввести силу инерции , то уравнение (6.1) можно записать в форме равновесия сил или k = l,2,...,N)Выражение соответствует принципу Д'Аламбера: совокупность всех внешних сил, действующих на механическую систему и сил инерции образует в каждый момент времени уравновешенную систему сил.Мысленно зафиксируем время t и сообщим каждой точке системы одно из возможных перемещений . Умножим скалярно каждое слагаемое уравнения (6.2) на , затем сложим все N полученных уравнений между собой, получим , т.е. , (k = l,2,...,N), (6.3)здесь: . - элементарная работа внешних сил, на одном из возможных перемещений - элементарная работа сил инерции на том же возможном перемещении.Уравнение (6.3) называется общим уравнением динамики: при движении механической системы в каждый момент времени сумма элементарных работ всех действующих на систему внешних сил и сил инерции на любом возможном перемещении равна нулю.Так как в уравнение (6.3) входит работа сил инерции, величина которой выражается через ускорение точек системы , то эти уравнения дают возможность составлять дифференциальные уравнения движения механической системы.Если механическая система представляет собой абсолютно твердое тело и это тело движется поступательно, то множество сил инерции точек тела следует заменить главным вектором сил инерции, приложенным к центру масс этого тела и равным

68. Если механическая система представляет собой абсолютно твердое тело и это тело движется поступательно, то множество сил инерции точек тела следует заменить главным вектором сил инерции, приложенным к центру масс этого тела и равным здесь М- масса тела, а_с =d²r_c/dt² ускорение центра масс тела.

69.   В классической механике впервые лагранжиан определен как разность между Т кинетической энергией и потенциальной энергией , то есть . Это определение не распространялось на нелинейные системы.Можно разложить  на две функции, которые будут справедливы и для нелинейных случаев.

Если лагранжиан , то дифференциал от    .            Поскольку  по определению – силовая функция, то для нахождения ее можно выбрать путь интегрирования так, что при интегрировании по  все  остаются постоянными, а при интегрировании по  постоянны все . Кроме того, интегрирование можно выполнять для определенного значения времени :  .            (1.145)

Подставляя в (1.145)  из уравнения (1.144), получаем при указанных изменениях переменных: Первая из функций в правой части (1.146) зависит от  и  и совершенно не зависит от скоростей системы . Она точно равна потенциальной энергии, взятой со знаком минус. Поэтому обобщенная сила а потенциальная энергия  определяется как (сравните с уравнением (1.106)).

Второе слагаемое в правой части (1.146) является функцией конечных значений координат  и скоростей . В линейном случае оно по форме точно соответствует кинетической энергии в механике или запасенной энергии для системы катушек индуктивностей, если .В нелинейном случае для электромеханических систем уравнение вида определяет магнитную коэнергию.

Поэтому, определяя обобщенный импульс как

для коэнергии  получим: (1.150)

В соответствии с (1.148) и (1.150) лагранжиан принимает вид:

 

 .      (1.151)Такое определение лагранжиана особенно ценно, поскольку оно используется при решении нелинейных задач, и в том числе – задач электромеханики.

В уравнении Лагранжа (1.143) определяют  как потенциальную силу, а  как импульс кинетических потенциалов.

70.,(i=1, 2, …, K)(7.16)Уравнения (7.16) носят название уравнений Лагранжа второго рода.

Величина - называется обобщенной скоростью; - обобщенным ускорением.

Уравнения Лагранжа второго рода (7.16) образуют систему из К обыкновенных дифференциальных уравнений второго порядка с К неизвестными. Напомним, что К - число степеней свободы рассматриваемой механической системы.

Итак, число уравнений Лагранжа второго рода равно числу степеней свободы системы.Уравнения Лагранжа дают единый и достаточно простой метод решения задач динамики и для простых и для сложных механических систем.При составлении уравнений (7.16) для заданной механической системы рекомендуется следующая последовательность действий:

• установить число степеней свободы системы и выбрать обобщенные координаты;

• изобразить систему в произвольном положении (обобщенные координаты должны быть положительными) и показать на рисунке все действующие на систему внешние силы;

• вычислить кинетическую энергию системы в ее произвольном движении и выразить ее через обобщенные координаты q_i, и обобщенные скорости ;

• выполнить предусмотренные уравнениями Лагранжа операции дифференцирования кинетической энергии системы;

• вычислить обобщенные силы, последовательно задавая элементарные положительные перемещения только соответствующей обобщенной координате;

• подставить все полученные выражения в уравнениях Лагранжа и решить полученную линейную систему К уравнений относительно К неизвестных обобщенных ускорений:

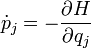
• 71. Уравнения Гамильтона (канонические) в физике и математике — система дифференциальных уравнений: 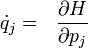- всего 2N дифференциальных уравнений первого порядка (j = 1, 2, ..., N) для динамической системы, описываемой N (обобщенными) координатами, являющиеся уравнениями движения системы (одной из форм таких уравнений, наравне с уравнениями Лагранжа, являющейся обобщением ньютоновских уравнений движения), где - 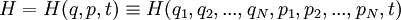так называемая функция Гамильтона, также иногда именуемая гамильтонианом, а точкой над p и q - обозначена производная по времени.Уравнения Гамильтона широко используются в гамильтоновой механике и других областях теоретической физики и математики.

72. Равновесие, или баланс, некоторого числа связанных явлений в естественных и гуманитарных науках.Система считается находящейся в положении равновесия, если все воздействия на эту систему компенсируются другими. Сходное понятие — устойчивость. Равновесие может быть устойчивым, неустойчивым или безразличным.Характерные примеры равновесия: Механическое равновесие, также известно как статическое равновесие, — состояние тела, находящегося в покое, или движущегося равномерно, в котором сумма сил и моментов, действующих на него, равна нулю.