35. Предмет динамики. Основные понятия и определения: масса, материальная точка, сила. Постоянные и переменные силы. Законы классической механики. Инерциальная система отсчета

ДИНАМИКА-Динамика изучает виды движения тела в зависимости от приложенных сил.

Аксиомы динамики:

1. всякая изолированная точка находится в состоянии относительного покоя, или равномерного прямолинейного движения до тех пор, пока приложенные силы не выведут её из этого состояния.

2. Ускорение тела прямопропорциональных действующей на тело силе.

3. Если на тело действует система сил, то его ускорение будет складываться из тех ускорений, которые бы тело получало от каждой силы в отдельности.

4. Всякому действию есть есть равное по величине и противоположно направлению противодействие.

Центр тяжести - это точка приложения силы тяжести, при повороте тела центр тяжести не меняет своего положения. Сила инерции - всегда направлена в противоположную сторону ускорению и приложена к связи.

Pu = -ma

При равномерном движении, т.е. когда а=0 сила инерции равна нулю.

При криволинейном движении раскладывается на две составляющие: на нормальную силу и на касательную.

Put=mat=mЕr

Pun=man=mw2r

Метод кинематики: условно прикладывают к телу силу инерции можно считать, что внешние силы реакции связей и сила инерции образуют уравновешенную систему сил.

F+R+Pu=0

Мощность - величина, равная отношению работы к промежутку времени, в течении которого она совершается

Материальная точка - это тело, формами и размерами которого можно пренебречь, но которое обладает массой

36. Основной закон динамики. Задачи динамики для свободной и несвободной материальной точки. Дифференциальные уравнения движения точки и их интегрирование.

Законы Ньютона

1. Каждое тело пребывает в состоянии покоя или равномерного прямолинейного движения до тех пор, пока действующие на тело силы не заставят его изменить движение (причиной изменения движения является сила).

2. Ускорение пропорционально приложеной силе и направлено по прямой, по которой действует сила: (количественная мера действия силы)

3. Силы взаимодействия двух материальных точек равны по величине и противоположны по направлению (сила всегда имеет материальный источник, который испытывает обратное действие объекта, к которому приложена сила)

Динамика является наукой об ускоряющих силах и о тех движениях, которые эти ускоряющие силы могут вызвать.2 з.Ньютона Сила может быть функцией . Эти три дифференциальных уравнения 2^го порядка имеют общее решение, зависящее от шести произвольных постоянных, определяемых из начальных условий.

Аксиома о суперпозиции сил.При одновременном действии на материальную точку нескольких сил ускорение точки относительно ИСО от действия каждой отдельной силы не зависит от наличия других приложенных к точке сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.

Между силами нет взаимного влияния друг на друга в создании ускорения точки: ; ; ; Все это справедливо для небольших скоростей .Размерностью силы является в системе СИ ньютон ([F]=н). Сила в 1н равна силе, сообщающей телумассой 1 кг ускорение, равное 1 м/с² - равнодействующая, Декартова система координат: Естественная система координат: Второе уравнение можно преобразовать: Получаем для естественной системы координат:

Первая (прямая) задача динамики точки: зная массу точки и ее закон движения, можно

найти действующую на точку силу. Зная проекции силы на координатные оси, легко определить модуль силы и косинусы углов силы с осями координат.

Пример: x=aCoskt; y=bSinkt, точка массы m. - эллипс с полуосями a, bF_x= -mk²aCoskt; F_y= -mk²bSinkt или F_x= -mk²x; F_y= -mk²y (r-радиус-вектор точки)Косинусы углов силы F с осями координат: Отсюда можно заключить, что сила F имеет направление, противоположное вектору r.Окончательно

Вторая (обратная) задача динамики точки: по заданой массе и действующей на точку

силе необходимо определить движение (закон движения) точки,

Для нахождения уравнений движения точки в декартовых координатах необходимо проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка. Решение системы содержит шесть произвольных постоянных С₁,C₂,C₃,C₄,C₅,C₆.

Каждая из координат x,y,z движущейся точки после интегрирования системы зависит от времени и всех шести постоянныхx=f₁(t, С₁,C₂,C₃,C₄,C₅,C₆); y=f₂(t, С₁,C₂,C₃,C₄,C₅,C₆); z=f₃(t, С₁,C₂,C₃,C₄,C₅,C₆)

Если продифференцировать решения, то для скоростей будем иметь: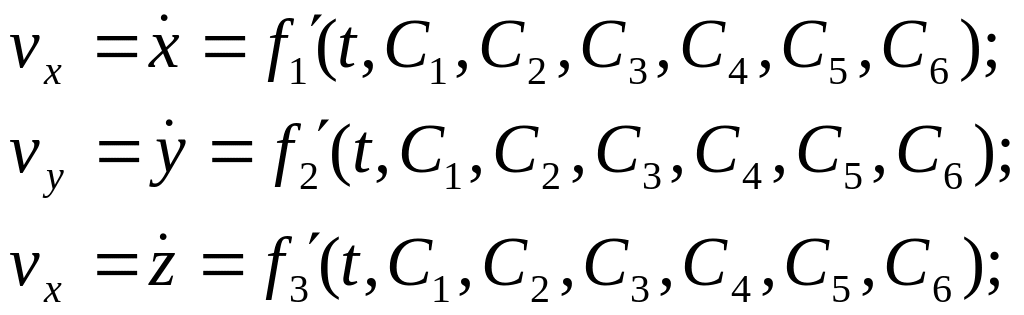 Таким образом, действующая сила однозначно определяет только ускорение точки и задает целый класс движений, траектории которых и скорости зависят от начального положения и скорости.

Для определения конкретного вида движения необходимо задать начальные условия: в некоторый момент времени t₀ (t=0).Используя эти условия получаем шесть уравнений для определения произвольных постоянных:

Начальные условия определяют единственное решение системы дифференциальных уравнений.

При движении точки в плоскости Oxy имеется два дифференциальных уравнения движения. В решения этих уравнений входят четыре произвольные постоянные, которые определяются из начальных условий:

Для прямолинейного движения имеется только одно уравнение и в его решение входят две произвольные постоянные, определяемые из начальных условий:

Задача интегрирования системы дифференциальных уравнений в общем случае является довольно трудной. Даже для одномерного случая решение удается выразить точно в квадратурах лишь при определенной зависимости силы от t, x и v.