Изменение риска

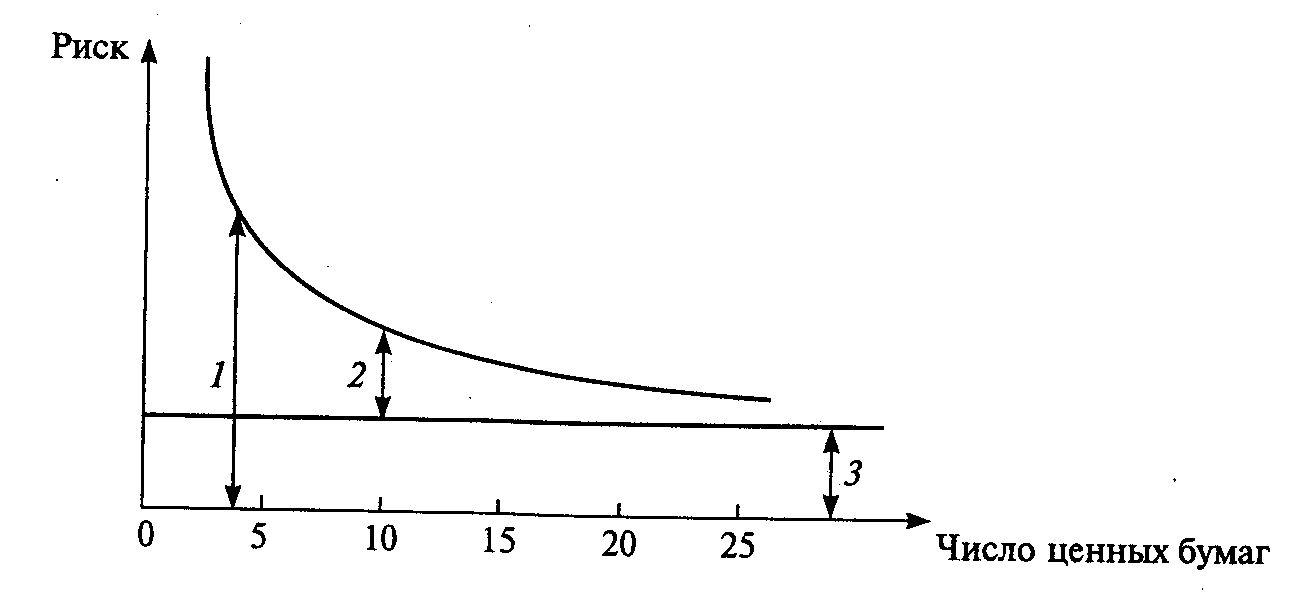
1 – Общий риск; 2 – Специфический (несистематический) риск; 3 – Систематический риск

Как показывает график, с увеличением числа активов в портфеле уменьшается специфический риск. Подавляющая часть несистематического риска устраняется при включении в портфель 15—20 видов ценных бумаг. Ценные бумаги различных эмитентов по-разному реагируют на изменение общеэкономической ситуации. Одни акции более устойчивы к колебаниям рынка, другие менее. Те ценные бумаги, которые изменяются в большей степени, чем меняется рынок, обладают повышенной чувствительностью. В связи с этим систематический риск конкретной ценной бумаги отличается от систематического риска для рынка в целом.

Мерой систематического риска является коэффициент β (β-фактор), который показывает уровень изменчивости актива по отношению к рынку (усредненному активу). В качестве рыночного портфеля берутся фондовые индексы, включающие в себя акции наиболее крупных компаний. В США такими индексами являются S&Р-50О, индексы Доу-Джонса, индекс Нью-йоркской фондовой биржи; в Великобритании — семейство индексов FТ; в Японии— индексы NIККЕI, в Германии — индексы DАХ; в России — индекс РТС (Российской торговой системы) и сводный индекс ММВБ (Московской межбанковской валютной биржи). Коэффициент β рассчитывается по формуле:

βi =σi / σm * Corr i m

где β - коэффициент i-го актива (портфеля); σi — стандартное отклонение доходности i-го актива (портфеля); σm — стандартное отклонение доходности по рынку в целом; Сorr i m — корреляция доходности i-го актива (портфеля) с доходностью рыночного портфеля.

Пример расчета коэффициента β.

Коэффициент корреляции вводится в формулу, чтобы учесть тесноту связи между активом и рынком (другим активом). Финансовый актив может иметь высокое знание σ, но это еще не означает, что данный актив намного рискованнее рыночного портфеля. Если отклонения актива и рыночного портфеля синхронизированы во времени, то эти отклонения могут взаимно гасить друг друга, уменьшая риск. Если σ актива и σ портфеля изменяются синхронно, то большее значение стандартного отклонения свидетельствует о большей степени риска.

Для определения степени взаимосвязи и направления изменения доходностей двух активов используют два показателя: коэффициент ковариации (COV AB) и коэффициент корреляции (Corr AB).

Показатель ковариации доходностей двух активов А и В рассчитывается по формуле:

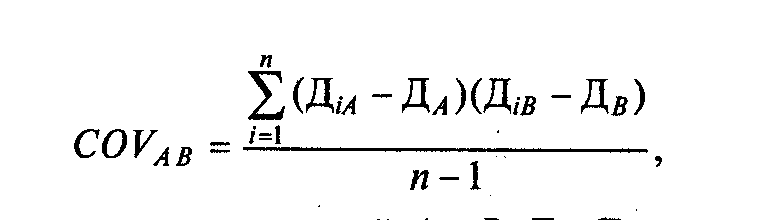
где COVAB - ковариация доходностей A и B; ДА, ДВ — средние доходности активов А и В за п периодов; ДiА,ДiВ — доходность активов А и В в i-м периоде; п — число периодов наблюдений.

Ковариация может иметь как положительное, так и отрицательное значение. Первое свидетельствует, что доходности активов изменяются в одном направлении. Отрицательное значение говорит, что доходности активов изменяются в противоположных направлениях. Если ковариация равна 0, то это означает, что взаимосвязь между доходностями активов отсутствует.

Другим показателем степени взаимосвязи двух активов является коэффициент корреляции:

где COVAB — ковариация доходностей активов А и В; σA— стандартное отклонение доходности актива А; σB — стандартное отклонение доходности актива В.

Коэффициент корреляции изменяется в интервале от +1 до -1. Если Corr AB= 1, то это означает, что доходности изменяются абсолютно одинаково, между ними существует полная корреляция, т. е. доходности активов А и В имеют прямую функциональную зависимость (рис. 3.4).

Если коэффициент корреляции находится в интервале от 0 до +1, то это свидетельствует, что доходности активов изменяются в одном направлении при изменении рыночной ситуации. Пример положительной корреляции представлен на рис. 3.5.

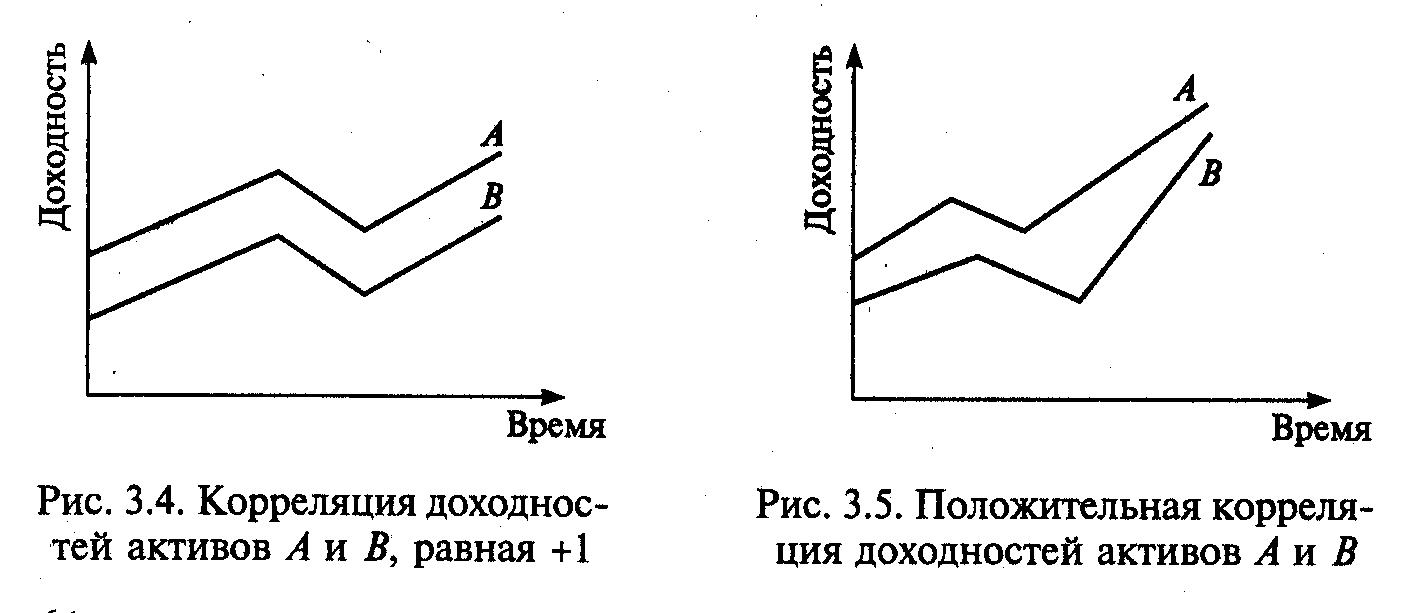
Когда коэффициент корреляции равен -1, то доходности двух активов изменяются в противоположном направлении. Если доходность по активу А растет, то доходность по активу В падает, и наоборот (рис.3.6).

Если корреляционная зависимость имеет отрицательное значение (от 0 до -1), то это свидетельствует, что при изменении ситуации на рынке доходности активов А и В изменяются в противоположном направлении.

В связи с тем, что между коэффициентом корреляции и показателем ковариации существует зависимость, выражаемая соответствующей формулой, коэффициент β, характеризующий изменчивость актива i по сравнению с рыночным портфелем (m), можно выразить или через коэффициент корреляции, или через показатель ковариации:

Рассмотрим теперь, как рассчитывается фактор β. В табл. 6 приведены фондовый индекс и цены акции компании А.

За рассматриваемый период дивиденды не выплачивались. Доход получен исключительно за счет роста курсовой стоимости акций. Поэтому доходность за равные периоды наблюдений (Д) рассчитывается по формуле:

где Рm — цена акции в периоде m; Рm-1 — цена акции в периоде, предшествующем m.

Для расчета доходности по рынку в целом берется значение фондового индекса. Результаты расчетов доходности представлены в табл. 7. Определим среднюю доходность акции компании А и рынка в целом, %:

ДА=(-1,72-0,76+5+3,64+1,08)/5=7,24/5=1,45

ДВ=(-7,25-1,25+5,38+5,41+1,42)/5=3,71/5=0,74

Если имеются статистические данные за предшествующий период, то дисперсия любого показателя (х) рассчитывается по формуле:

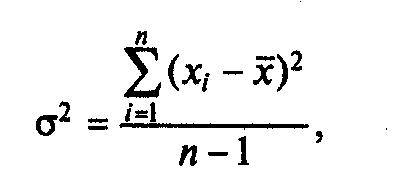где хi — конкретное значение показателя х в период i; xˉ — среднее значение показателя х за рассматриваемый период; n — количество периодов; i - 1, ... n — количество наблюдений.

таблица 6

Фондовый индекс и цены акций А

Показатель	Период наблюдений, г.
	1-й	2-й	3-й	4-й	5-й	6-й
Фондовый индекс Цена акций компании А, руб.	345 17,43	320 17,13	316 17,00	333 17,85	351 18,50	356 18,70

таблица 7