
- •Модель авторегрессии 1-го порядка - ар(1)
- •Продолжение табл. 5.7.2
- •5.8. Модель авторегрессии 2-го порядка - ар(2)
- •Теория очередей
- •Линейная сглаживающая функция
- •2.2. Параболическая и кубическая сглаживающие функции
- •Аналитическое выравнивание временных рядов
- •. Кривые роста и интерполирование
- •Кривые роста 1-го класса
- •1. Класс полиномов
- •2. Простая экспоненциальная (показательная) кривая
- •3. Логарифмическая парабола
- •Кривые роста 2-го класса
- •1. Модифицированная экспонента
- •§2.1. Аддитивная и мультипликативная модели
- •Классическая сезонная декомпозиция
- •§2.3. Проведение классической сезонной декомпозиции
- •Автокорреляционная функция (акф)
- •5.5. Частная автокорреляционная функция (чакф)
- •Финансовые решения в условиях риска
- •5.1. Динамические модели планирования финансов
Линейная сглаживающая функция
Пусть
имеется временной ряд
![]() ,
который локально может быть описан на
временном интервале 2m+1
линейной функцией вида
,
который локально может быть описан на
временном интервале 2m+1
линейной функцией вида
![]() (2.1.1)
(2.1.1)
где
![]() .
.
Для подбора коэффициентов воспользуемся критерием минимума для метода наименьших квадратов (МНК):
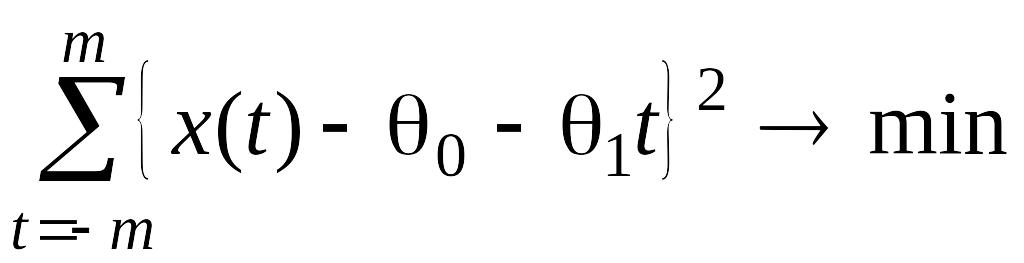 .
(2.1.2)
.
(2.1.2)
Откуда,
дифференцируя левую часть (2.1.2) по
параметрам
![]() и приравнивая значения полученных
частных производных нулю, получаем
систему уравнений для определения
параметров:
и приравнивая значения полученных
частных производных нулю, получаем
систему уравнений для определения
параметров:
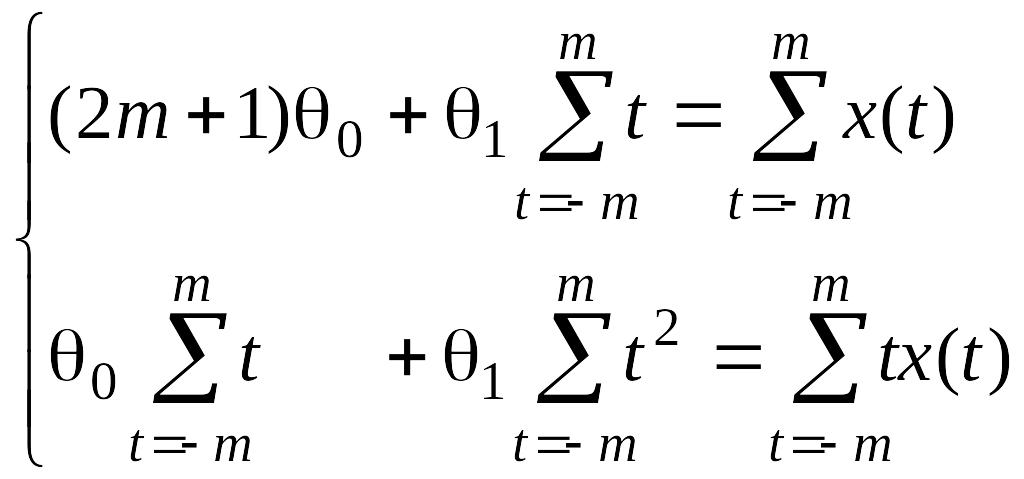 .
.![]() (2.1.3)
(2.1.3)
Так
как
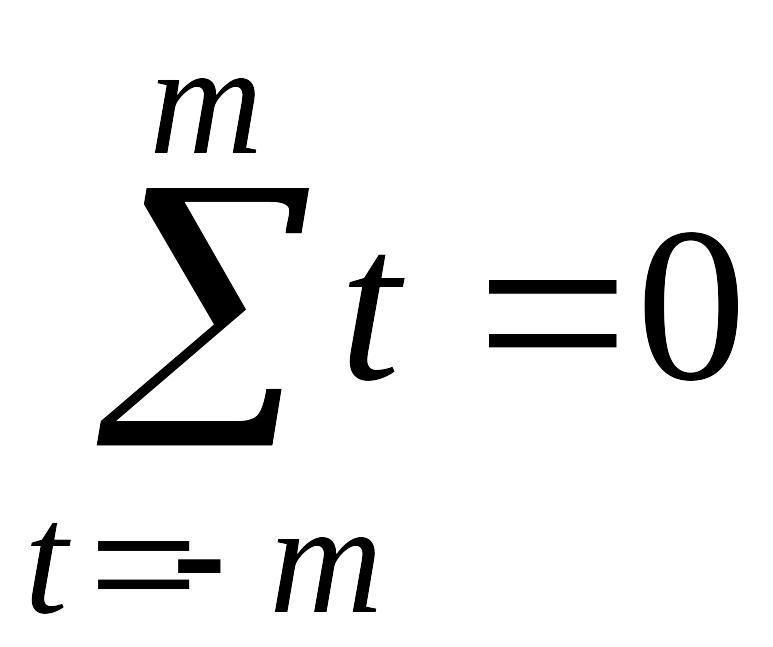 ,
то
,
то
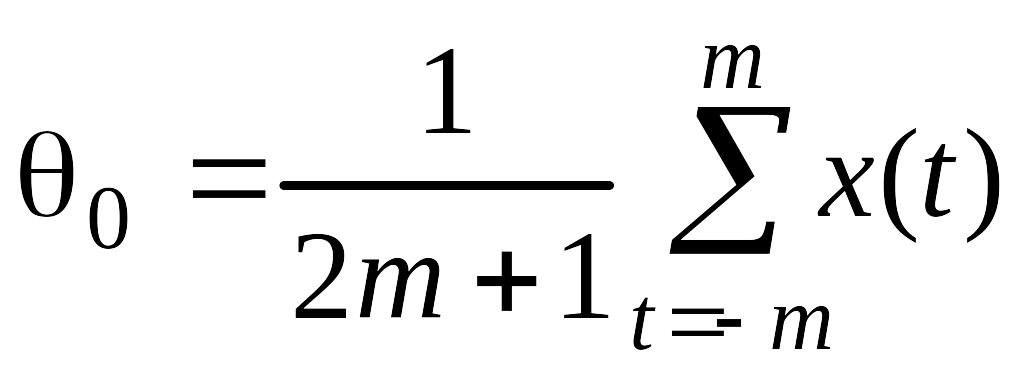 ,
(2.1.4)
,
(2.1.4)
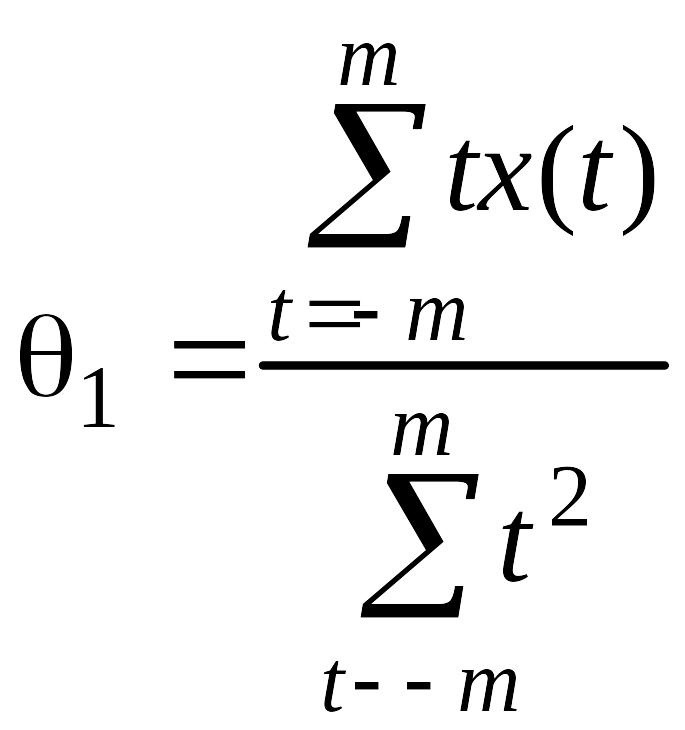 .
(2.1.5)
.
(2.1.5)
Оценка
сглаженного значения временного ряда
определяется в средней точке, т.е.
при t = 0,
поэтому из (2.1.1) вытекает, что
![]() .
Поэтому соотношение (2.1.4) означает, что
в качестве сглаженного значения надо
брать среднее арифметическое окаймляющих
его 2m+1
членов.
.
Поэтому соотношение (2.1.4) означает, что
в качестве сглаженного значения надо
брать среднее арифметическое окаймляющих
его 2m+1
членов.
Обычно
для описания алгоритма сглаживания
используются задания весовых коэффициентов
![]() для
первых его m+1
сглаживающих значений, так как
для
первых его m+1
сглаживающих значений, так как
![]() .
В данном случае эти значения
.
В данном случае эти значения
![]() .
(2.1.6)
.
(2.1.6)
2.2. Параболическая и кубическая сглаживающие функции
Пусть имеется временной ряд , который локально может быть описан на временном интервале 2m+1 параболической функцией вида
![]() (2.2.1)
(2.2.1)
или кубической функцией
![]() ,
(2.2.2)
,
(2.2.2)
где .
Снова воспользовавшись критерием минимума МНК для функций:
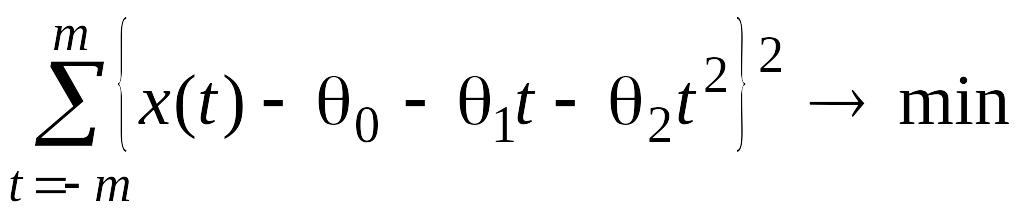 (2.2.3)
(2.2.3)
и
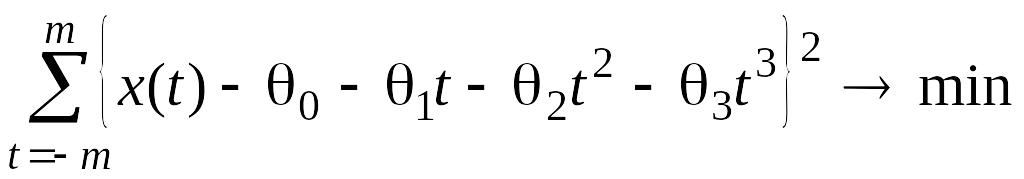 ,
(2.2.4)
,
(2.2.4)
получим соответствующие системы уравнений, которые мы будем рассматривать одновременно.
Из (2.2.3) имеем:
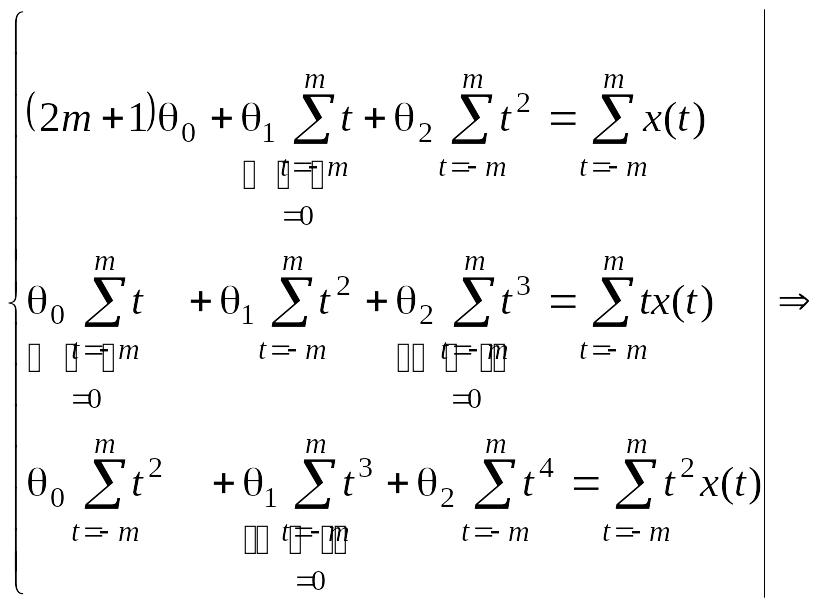
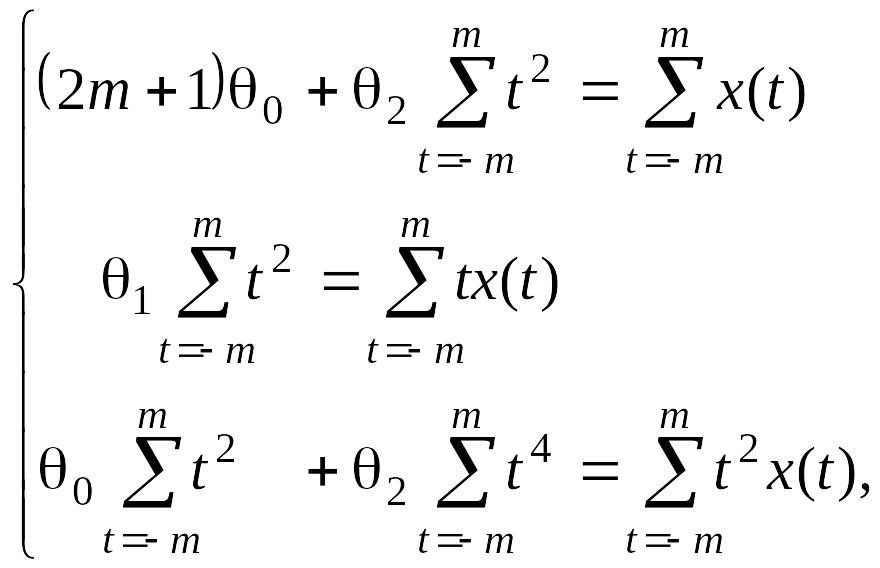 (2.2.5)
(2.2.5)
а из (2.2.4):
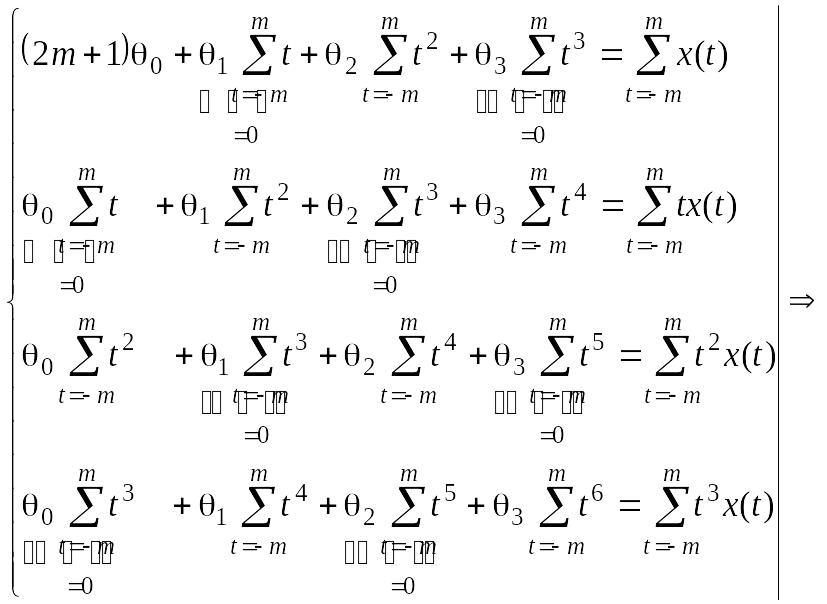
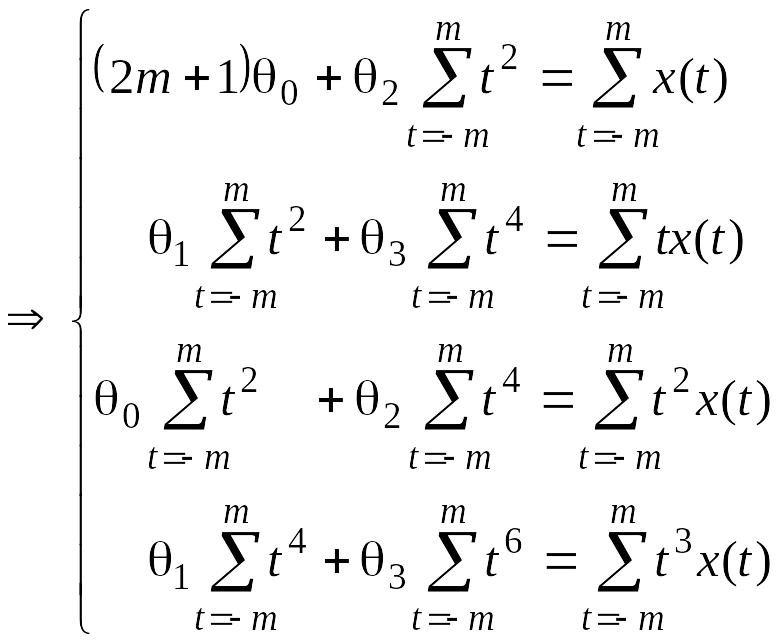 .
(2.2.6)
.
(2.2.6)
При
выводе соотношений (2.2.5) и (2.2.6) использовано
соотношение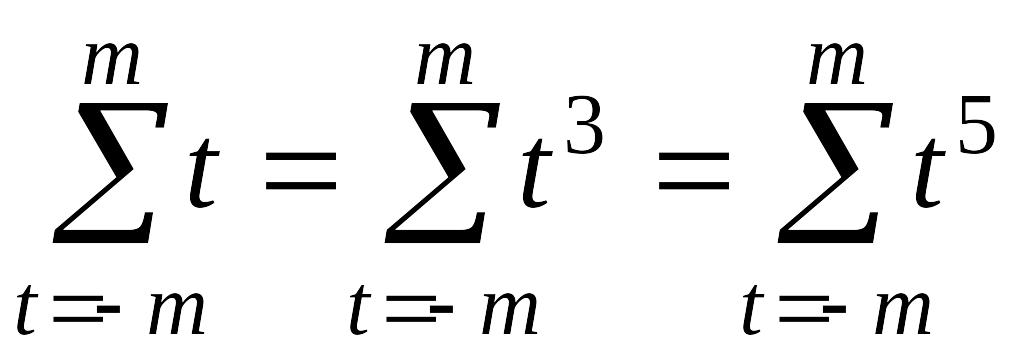 ,
действительное для заданного временного
интервала
.
,
действительное для заданного временного
интервала
.
Оценка
сглаженного значения временного ряда
определяется в средней точке, т.е.
при t
= 0, поэтому
из (2.2.1), как и из (2.2.2), вытекает, что
![]() .
Но, как нетрудно установить из систем
(2.2.5) и (2.2.6), определение параметра
.
Но, как нетрудно установить из систем
(2.2.5) и (2.2.6), определение параметра
![]() производится из 1-го и 3-го уравнений
соответствующих систем, которые
идентичны.
производится из 1-го и 3-го уравнений
соответствующих систем, которые
идентичны.
Выразив
из 3-го уравнения любой из систем параметр
![]()
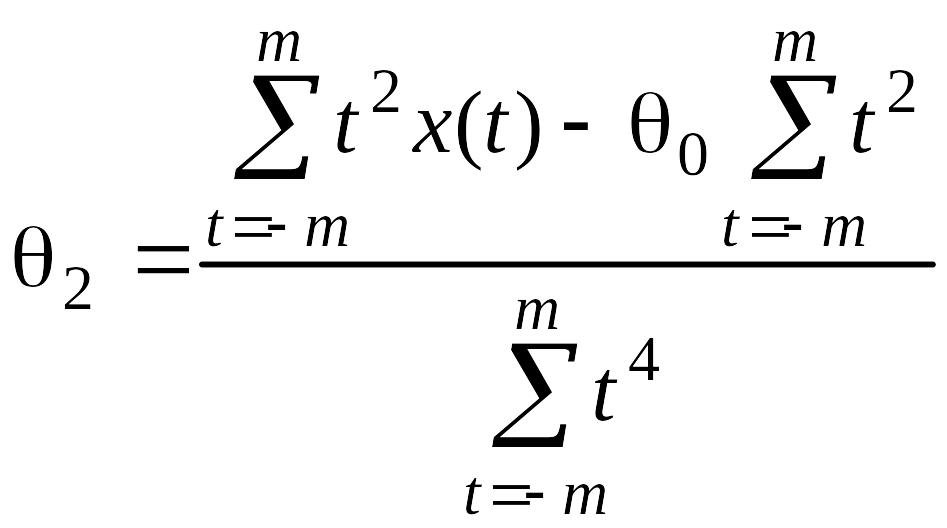
и подставив в 1-е уравнение, получим:
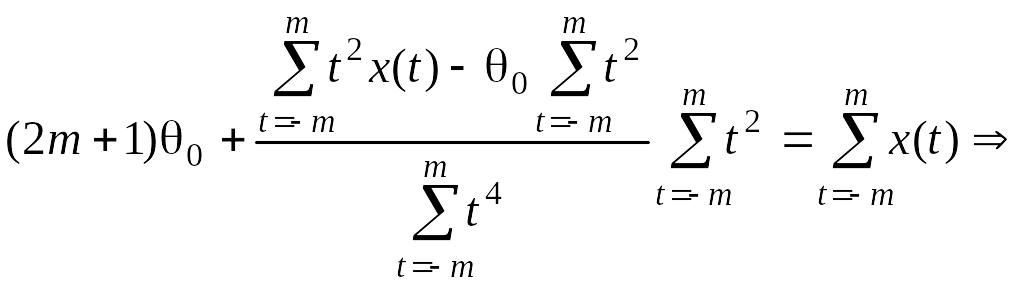
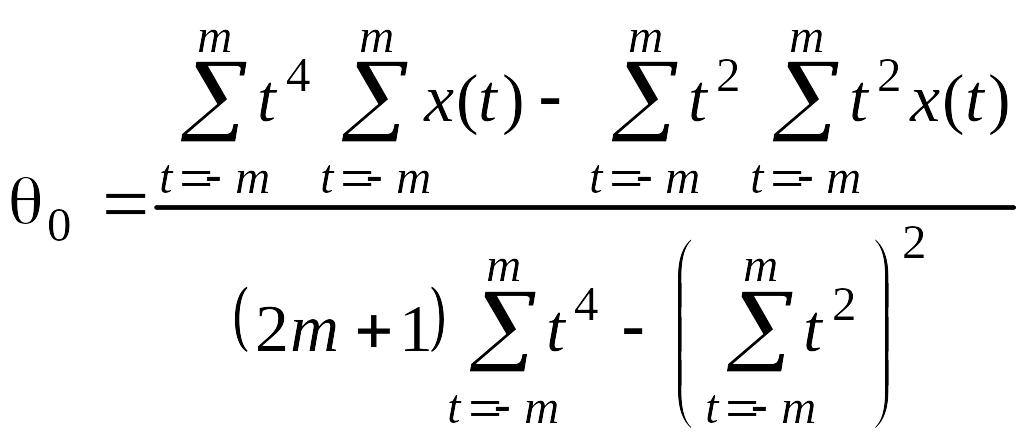 .
(2.2.7)
.
(2.2.7)
В зависимости от значения m получим значения сглаживающих коэффициентов.
При m=2 или длине усреднения 2m+1=5 имеем:
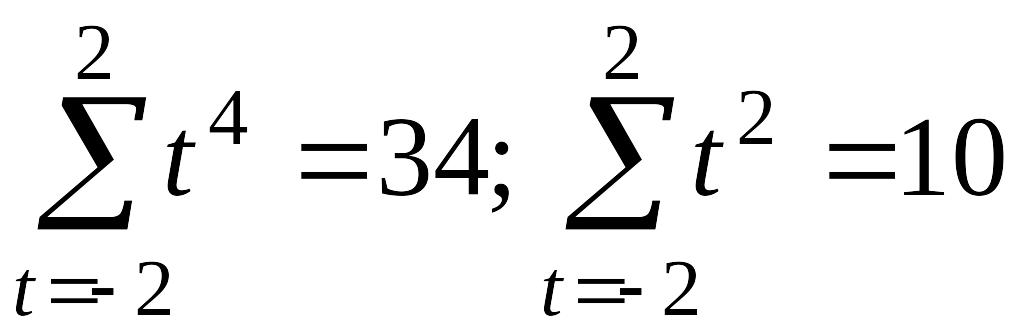 и
и
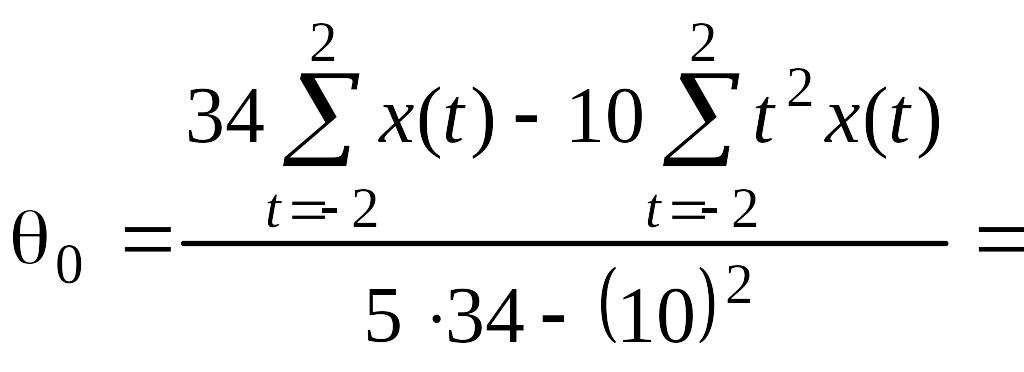
![]()
![]()
![]() .
(2.2.8)
.
(2.2.8)
При m=3 или длине усреднения 2m+1=7 имеем:
 и
и
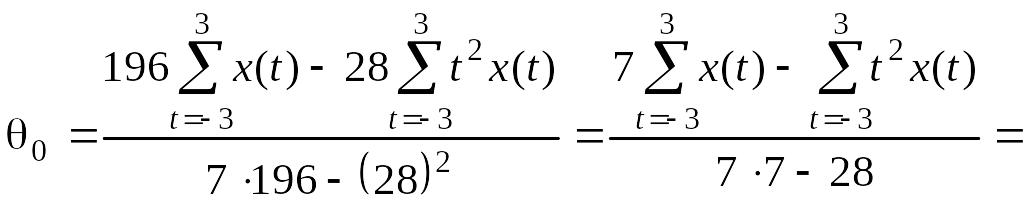
![]()
![]()
![]()
![]() .
(2.2.9)
.
(2.2.9)
При m=4 или длине усреднения 2m+1=9 имеем:
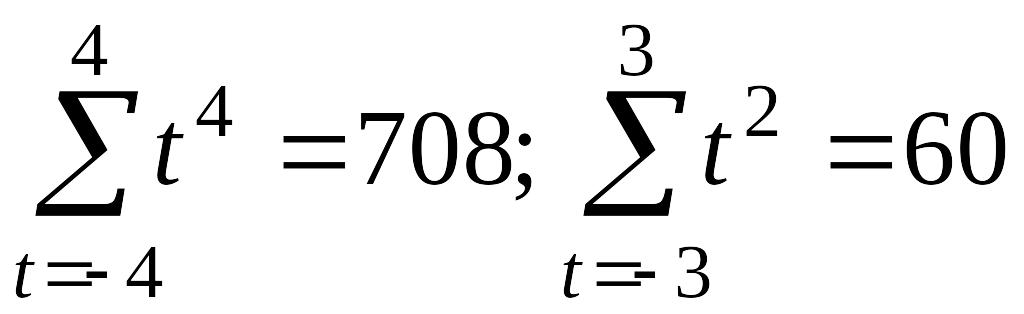 и
и
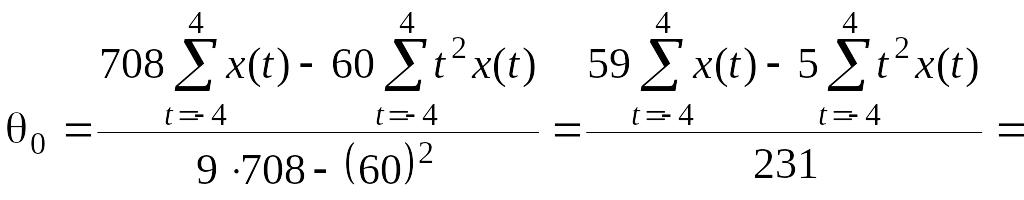
![]()
![]()
![]()
![]() .
(2.2.10)
.
(2.2.10)
Результаты (2.2.8),(2.2.9) и (2.2.10) объединены в табл. 2.2.1.
Таблица
2.2.1. Значения
весовых коэффициентов в формуле
![]() скользящего среднего для полинома
степени 2 и 3
скользящего среднего для полинома
степени 2 и 3
m |
Длина усреднения 2m+1 |
|
2 |
5 |
|
3 |
7 |
|
4 |
9 |
|
Из
симметричности преобразований для
получения коэффициентов
![]() следует, что
следует, что
![]() ,
поэтому коэффициенты
,
поэтому коэффициенты
![]() в таблице не показываются.
в таблице не показываются.
Однако при сглаживании по формулам табл. 2.2.1 m первыx и m последних значений ряда не могут быть получены. Для получения и этих значений необходимо проводить аппроксимацию по параметрам, полученным по 2m+1 первых либо последних значений исходного ряда с учетом соотношения (2.2.1) или (2.2.2).
Можно
даже получить соответствующие весовые
коэффициенты. Рассмотрим их построение
на примере параболического полинома
(2.2.1). Вернемся к системе (2.2.5) и определим
параметры
![]() .
.
Из 2-го уравнения системы (2.2.5) сразу получим
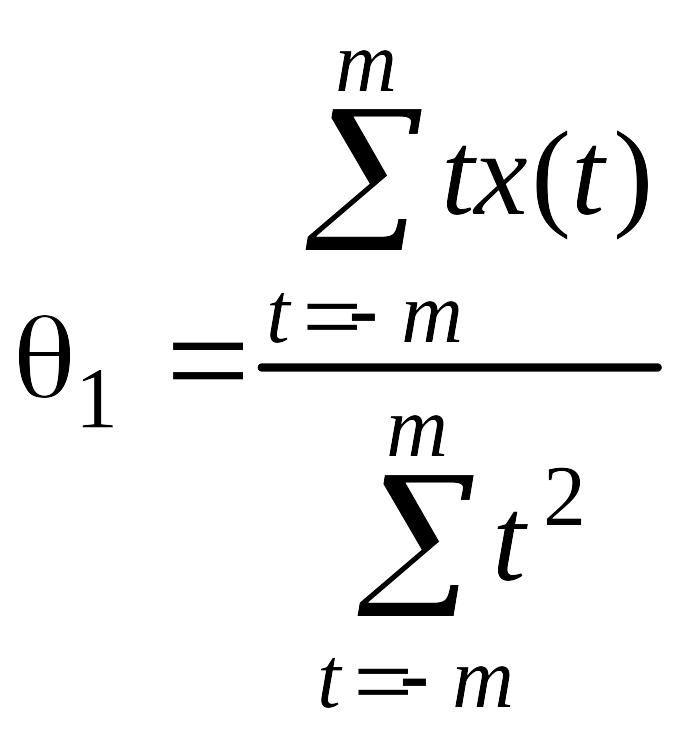 .
(2.2.11)
.
(2.2.11)
Выразив
![]() из 1-го уравнения (2.2.5)
из 1-го уравнения (2.2.5)
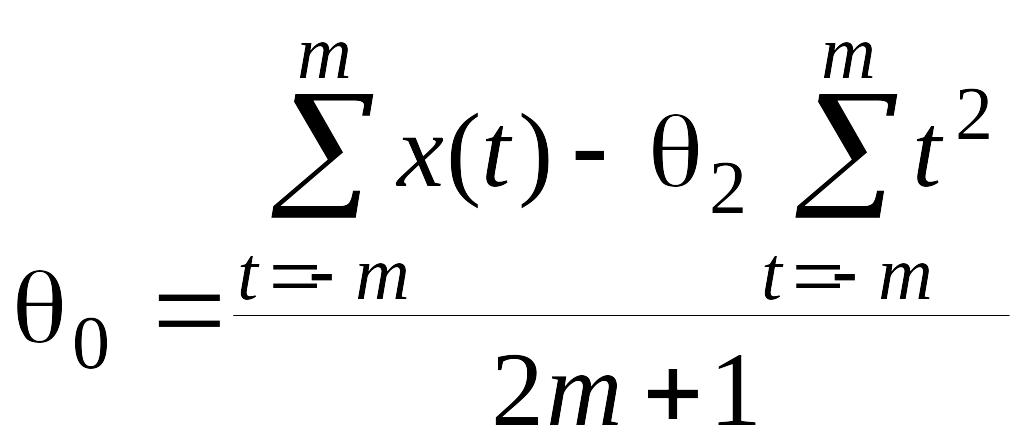
и подставим в 3-е уравнение (2.2.5):
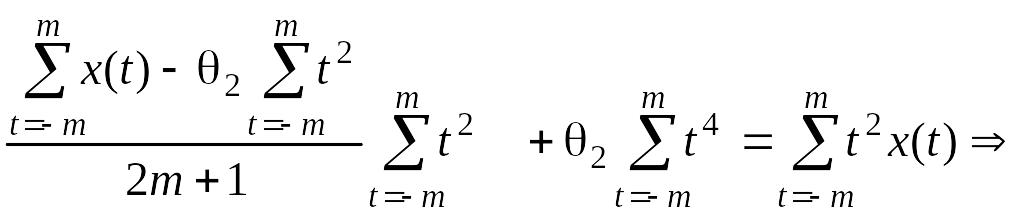
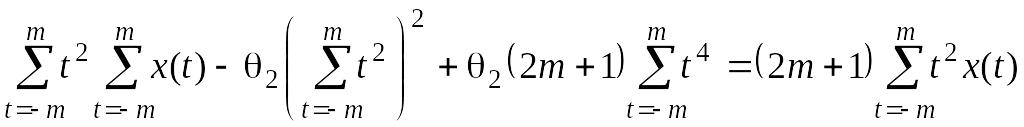
получим
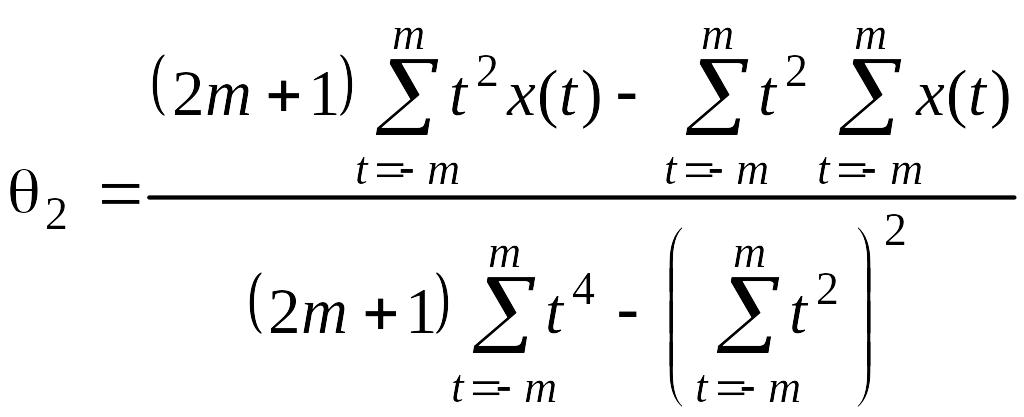 .
(2.2.12)
.
(2.2.12)
Для m = 2 тогда
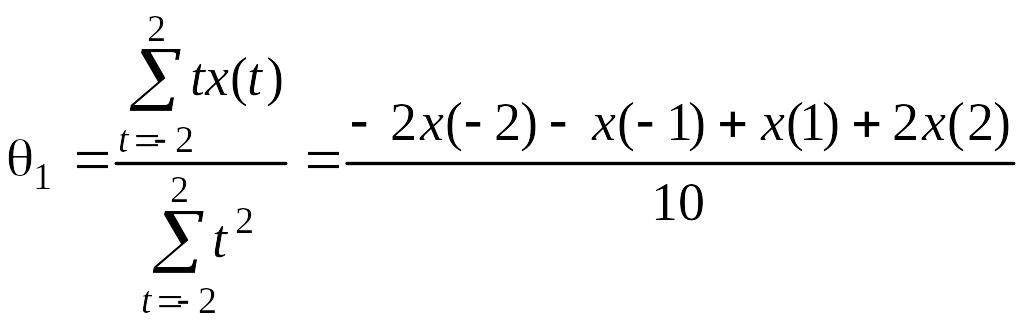 ,
(2.2.13)
,
(2.2.13)
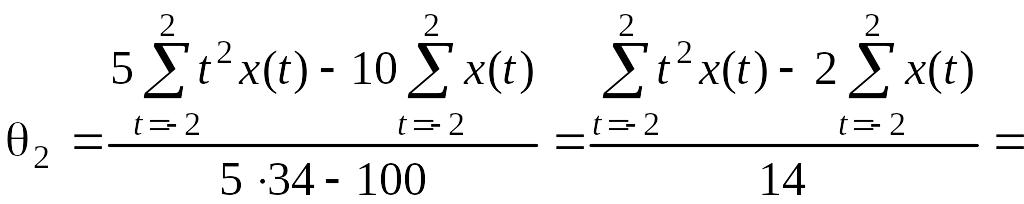
![]()
![]() .
(2.2.14)
.
(2.2.14)
Таким образом, параболический полином (2.2.1) для m = 2 можно записать с учетом коэффициентов из табл. 2.2.1, (2.2.13) и (2.2.14) так:
![]()
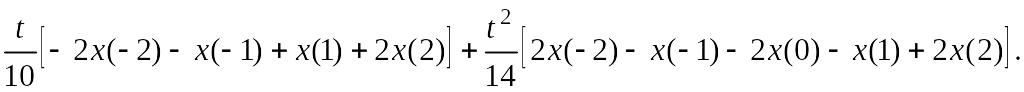 (2.2.15)
(2.2.15)
Используя (2.2.15), получим значения коэффициентов для t = -1, что соответствует значению 2-го члена сглаженного ряда:
![]()
![]()
![]()
![]()
![]() (2.2.16)
(2.2.16)
для t = 1, что соответствует значению предпоследнего члена сглаженного ряда:
![]()
![]()
![]() ,
(2.2.17)
,
(2.2.17)
для t = -2, что соответствует значению 1-го члена сглаженного ряда:
![]()
![]()
![]()
![]()
![]() (2.2.18)
(2.2.18)
и для t = 2, что соответствует значению последнего члена сглаженного ряда:
![]()
![]()
![]() (2.2.19)
(2.2.19)
Объединим (2.2.16) - (2.2.19) в табл. 2.2.2.
Таблица 2.2.2. Значения весовых коэффициентов в формуле скользящего среднего для полинома степени 2 и m=2 для крайних членов
-
№ п/п
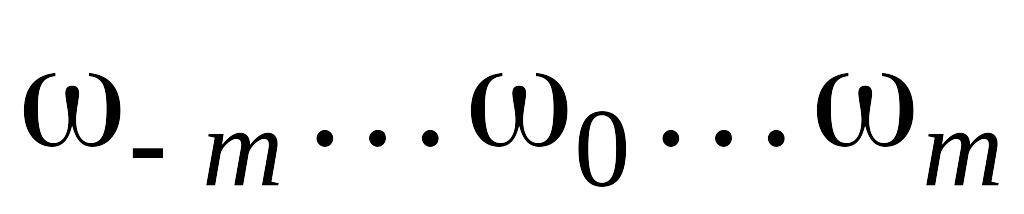
Первый
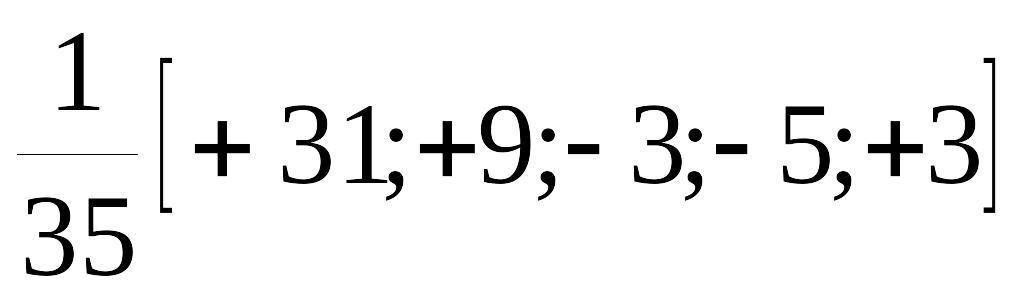
Второй
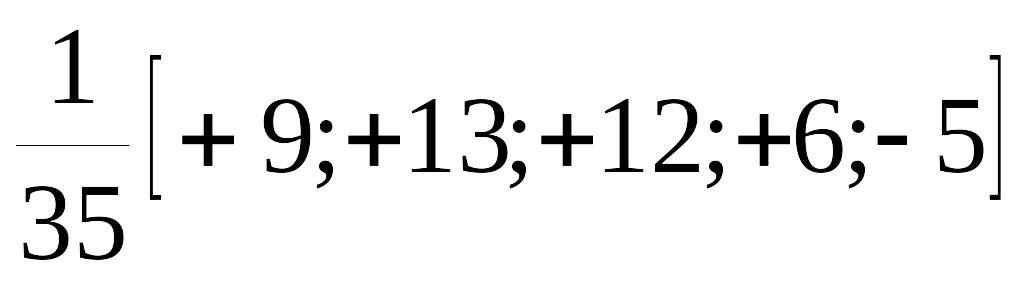
Предпоследний
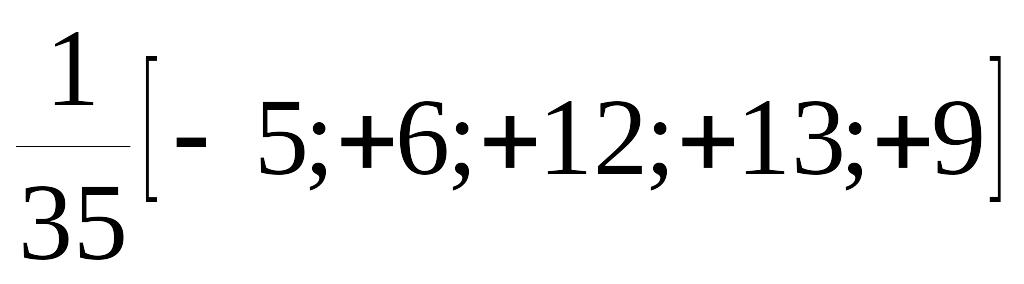
Последний
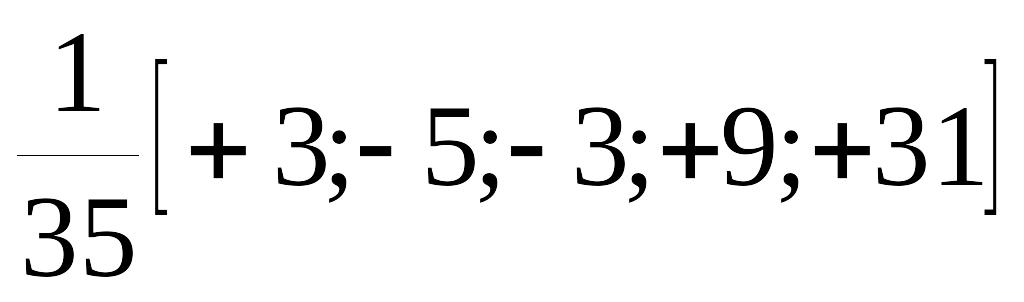
Для 1-го и последнего, а также для 2-го и предпоследнего нетрудно усмотреть симметричность коэффициентов.
