Теория очередей

В процессе управления возникают непрерывные потоки информации, которые в свою очередь обеспечивают процессы непрерывного движения материалов и готовых изделий между производителями и потребителями. Все эти процессы имеют характер непрерывных потоков, имеющих однако стохастический характер. Это приводит к возникновению как недоиспользования ресурсов, так и к их полной занятости, которая приводит к очередям заявок на обслуживание. Теория очередей, называемая в РФ достаточно часто теорией массового обслуживания, позволяет дать количественное описание данных процессов.

Данная теория основана на соотношении (5.2.7) в устоявшемся режиме, т.е. при . Иными словами, вектор p(t) является вектором стационарных вероятностей, который однозначно находится по заданной матрице интенсивностей R, элементы которой распределены по закону Пуассона

. (5.4.1)

При этом элементы вектора p(t), как и матрицы R, могут иметь различное смысловое значение в зависимости от того, какой процесс рассматривается.

Рассмотрим процесс, достаточно общего вида – многоканальную СМО с ограниченной длиной очереди, имеющую следующие характеристики:

n  – число каналов обслуживания;

m – число мест в очереди;

 – интенсивность поступления заявок (число поступающих заявок в 1 момент времени);

 – интенсивность обслуживания заявок;

 – интенсивность нагрузки.

Для построения матрицы R представим на рис. 5.4.1 нашу систему в виде так называемого размеченного графа состояний для легко обозримой размерности (n = 3; m = 2) со следующими состояниями:

 – все каналы обслуживания свободны;

 – 1 канал занят обслуживанием;

 – 2 канала заняты обслуживанием;

 – 3 канала заняты обслуживанием;

 – 3 канала заняты обслуживанием, в очереди 1 заявка;

 – 3 канала заняты обслуживанием, в очереди 2 заявки.

Рис. 5.4.1. Размеченный граф состояний для n = 3; m = 2

Для данного частного случая графа соотношение (5.4.1) будет выглядеть так:

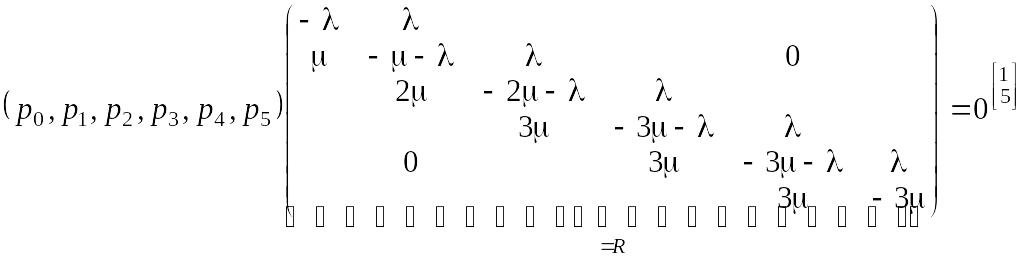
Рассмотрим, как был сформирован, например, 2-й столбец матрицы R, который определяет состояние . Итак, система находилась в состоянии с вероятностью и за время t не перешла в любое из смежных с ней состояний. В другие состояния система перейти не может в силу того, что рассматривается пуассоновский процесс, согласно которому за время t может произойти лишь одно событие. Вывести систему из состояния можно лишь суммарным потоком  + . Знак “минус” определяет интенсивность невыхода из состояния . В состояние можно прийти из смежного состояния при появлении заявки на обслуживание с интенсивностью  или из при завершении обслуживания одной заявки, интенсивность обслуживания которой с учетом возможной загрузки двух каналов равна 2.

Заметим также, что если до состояния (в данном случае 1-го) интенсивности обслуживания увеличиваются на величину , то, начиная с состояния вплоть до состояния , оно устанавливается равным максимальной интенсивности n, определяемой числом каналов обслуживания.

Теперь аналогично может быть записана и матрица R для произвольных значений n и m (внутри многоточий представлены столбцы для состояний и ):

.

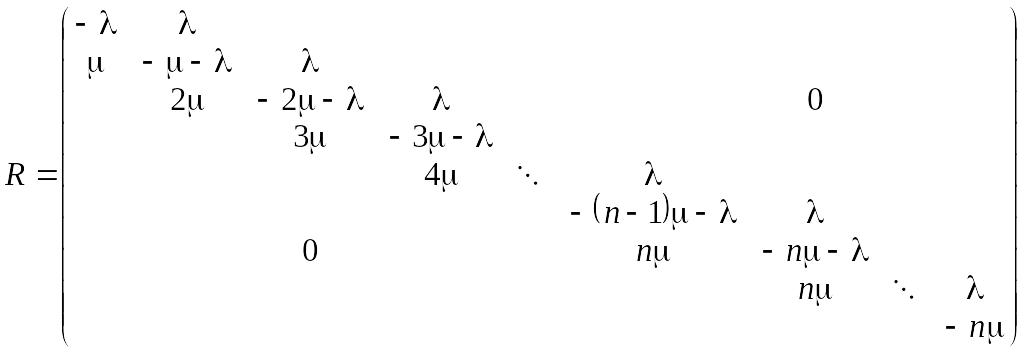Система линейных уравнений, построенная на основе соотношения (5.4.1) может быть записана в следующем виде (последнее уравнение далее приводится отдельно):

Из 1-го, 2-го, 3-го, 4-го уравнения системы имеем

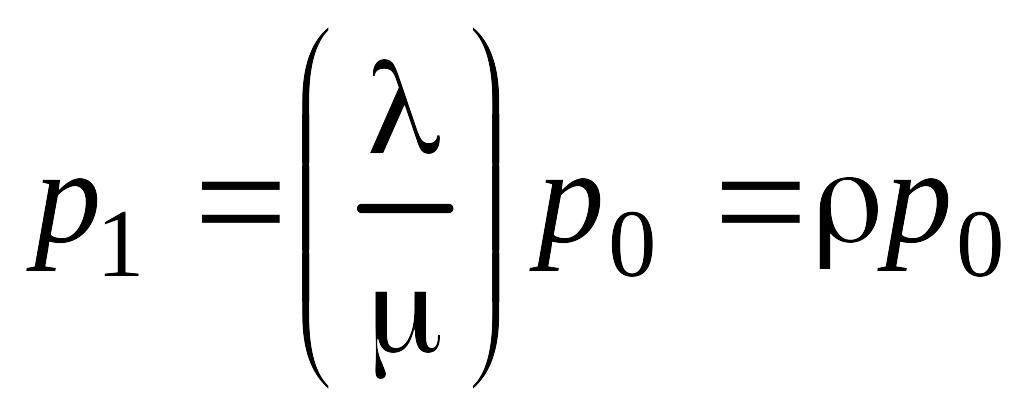; (5.4.2)

;

;

.

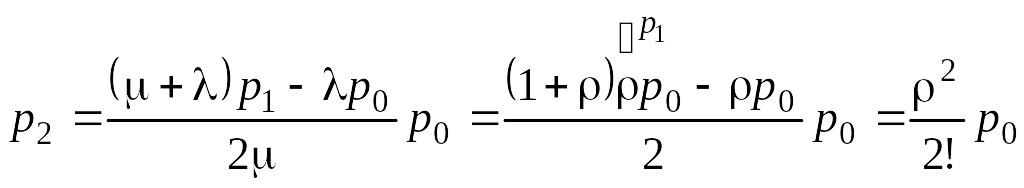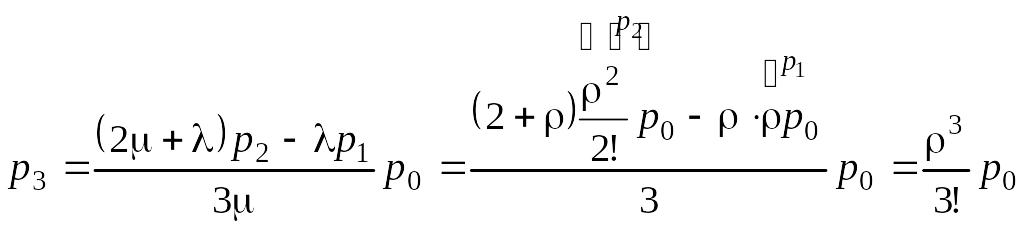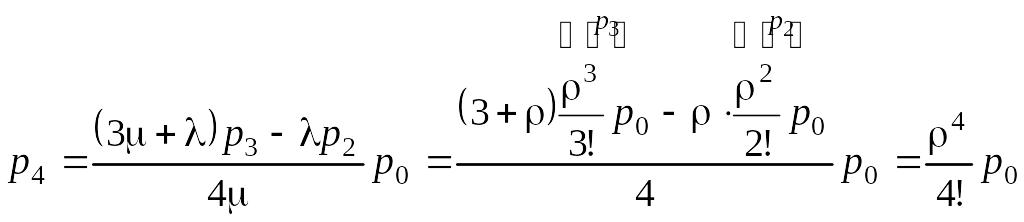Из n-го уравнения системы по индукции имеем

.

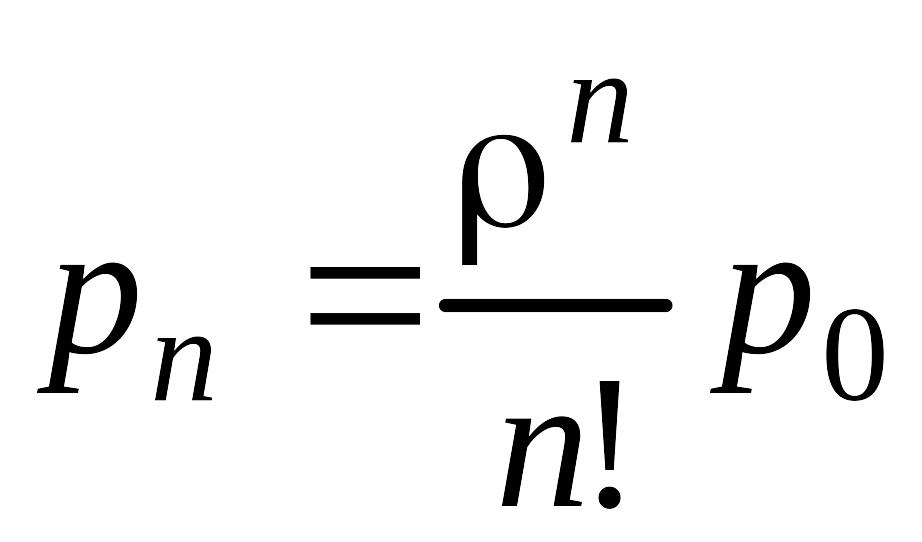Из (n+1)-го уравнения системы имеем

.

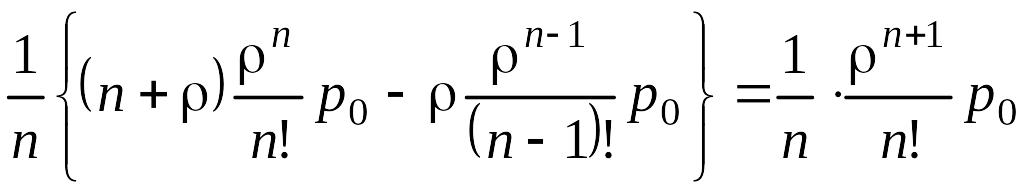Из (n+2) – го уравнения системы имеем

.

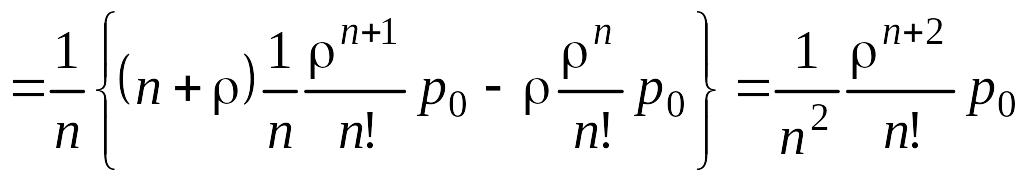Из (n + m)-го уравнения системы по индукции имеем

.

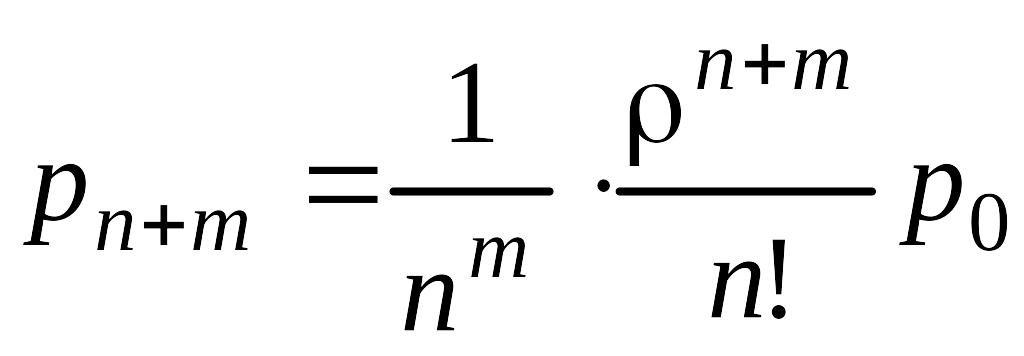Наконец, из последнего (n + m +1 )-го уравнения, которое имеет вид

,

также получим

.

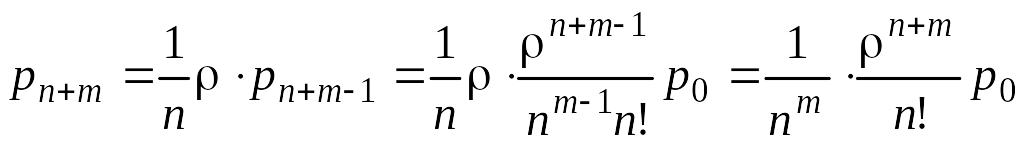Из 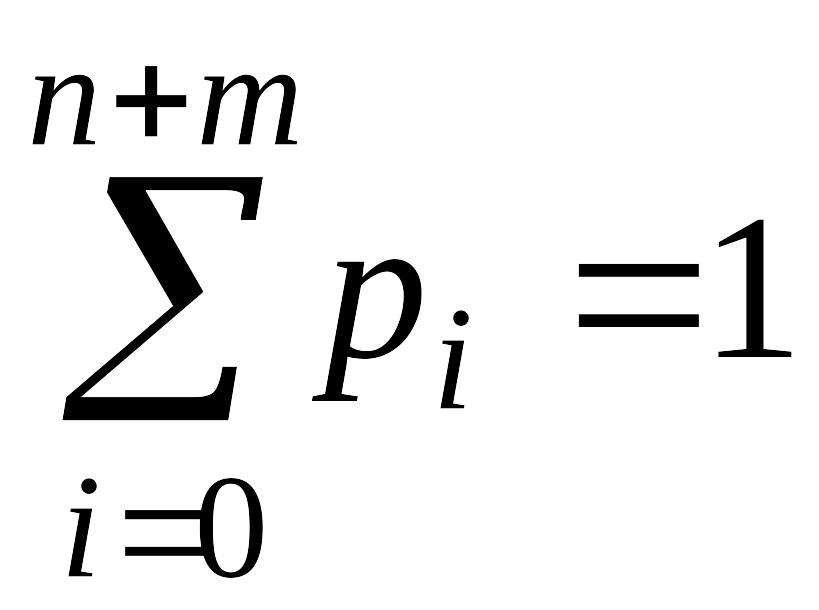определяем выражение для , которое характеризует долю простоя системы:

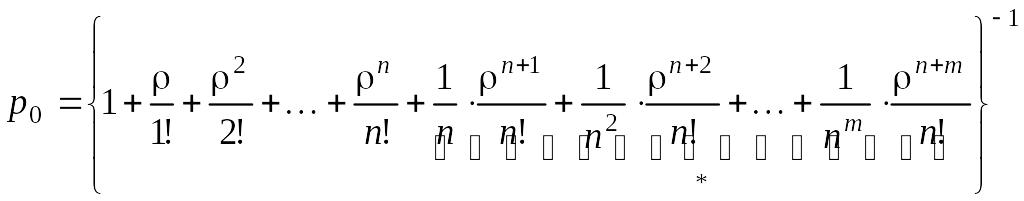. (5.4.3)

Элементы, выделенные *, при представляют собой геометрическую прогрессию со знаменателем и имеют сумму, равную величине

.

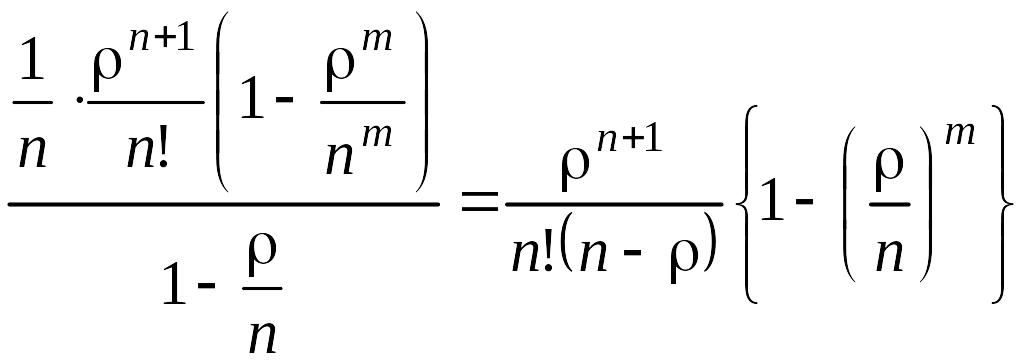Следовательно,

. (5.4.4)

Соотношение (5.4.3) при  = n может быть записано так:

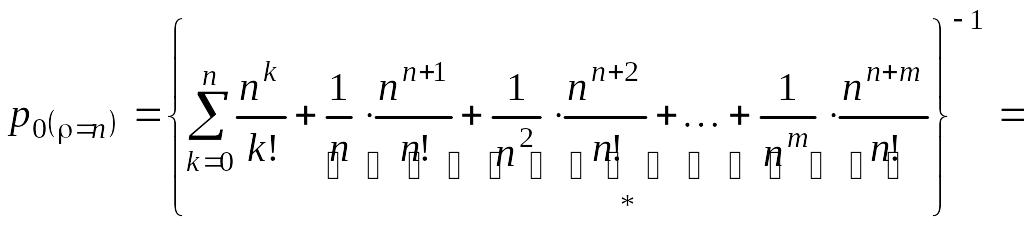
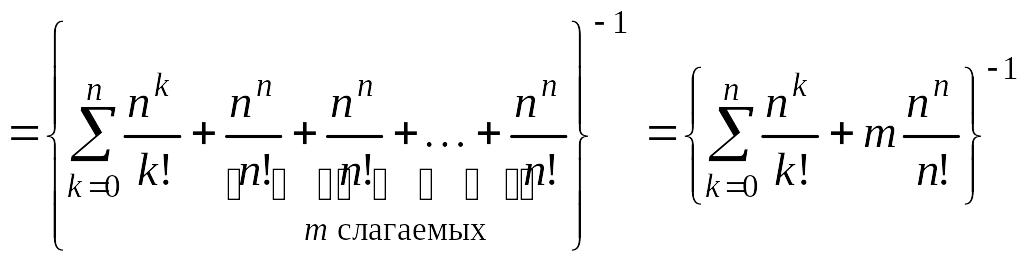. (5.4.5)

Вероятность отказа в обслуживании наступает тогда, когда все n каналов и все m мест в очереди заняты, т.е.

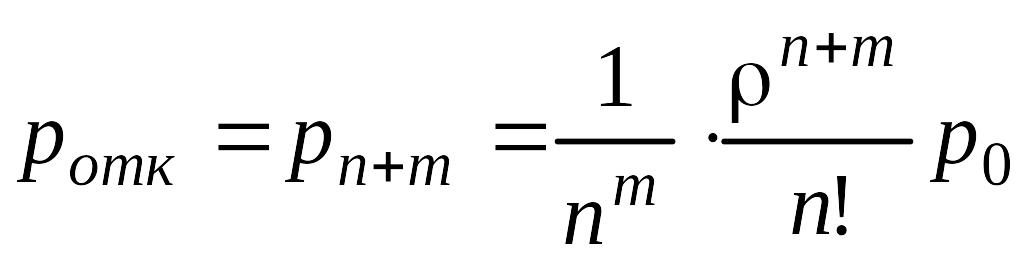. (5.4.6)

Длина очереди представляет собой математическое ожидание длин очередей для состояний, начиная с (n + 1)-го:

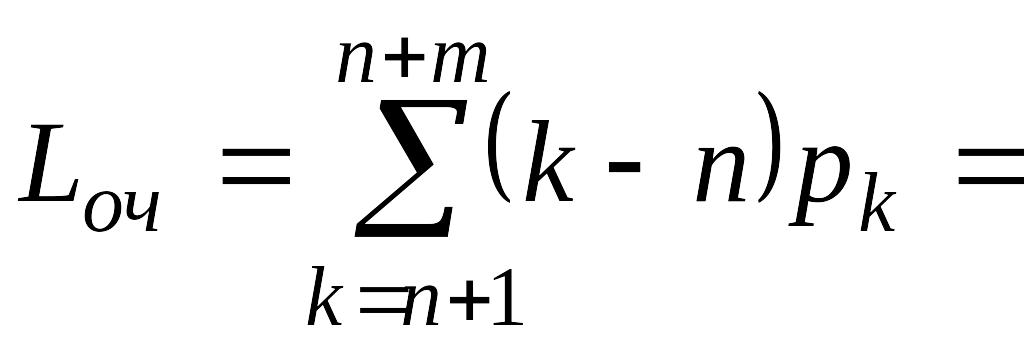
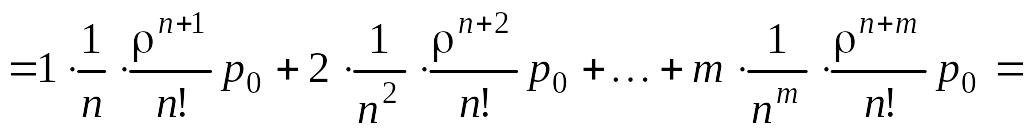
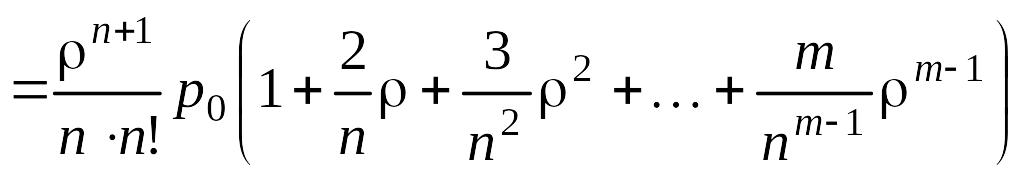. (5.4.7)

Сумма в скобках может быть представлена так:

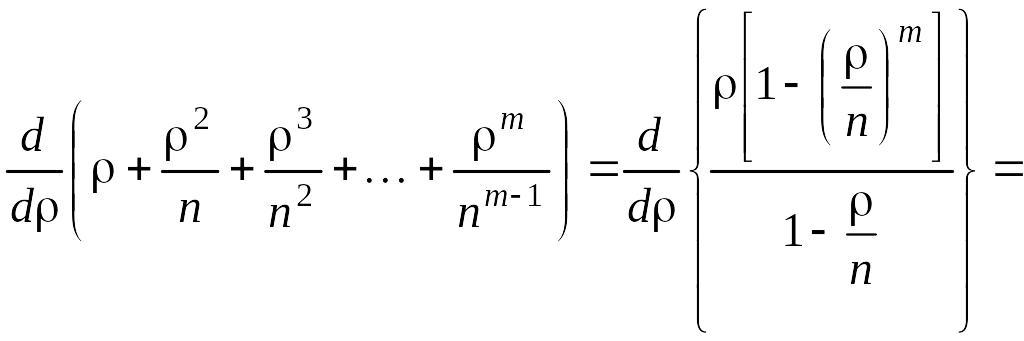
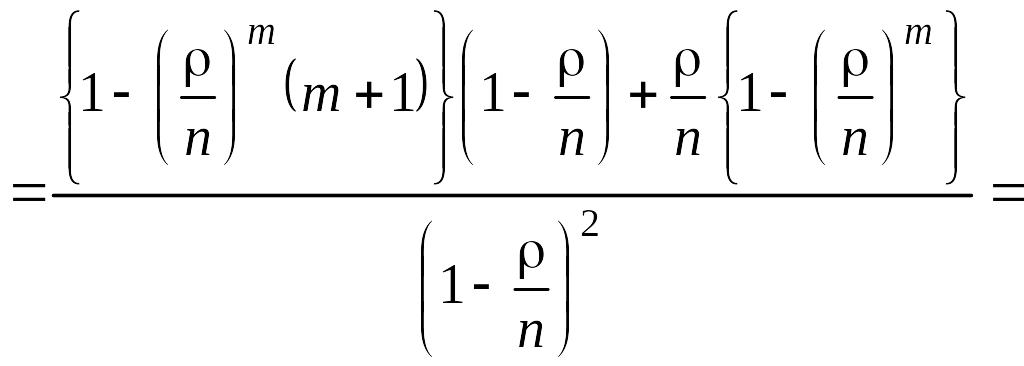
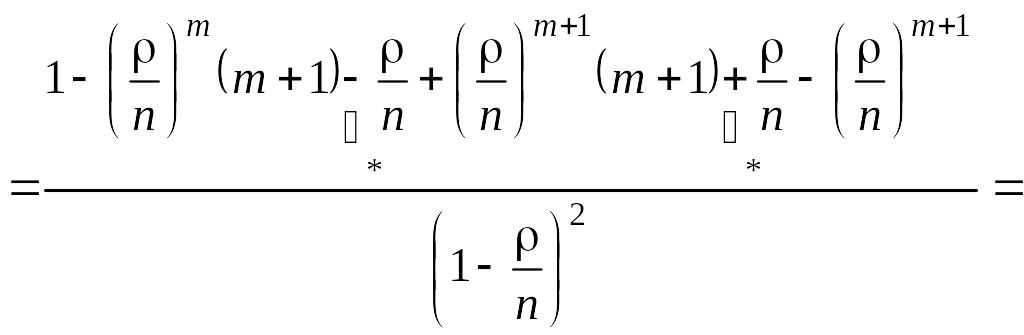
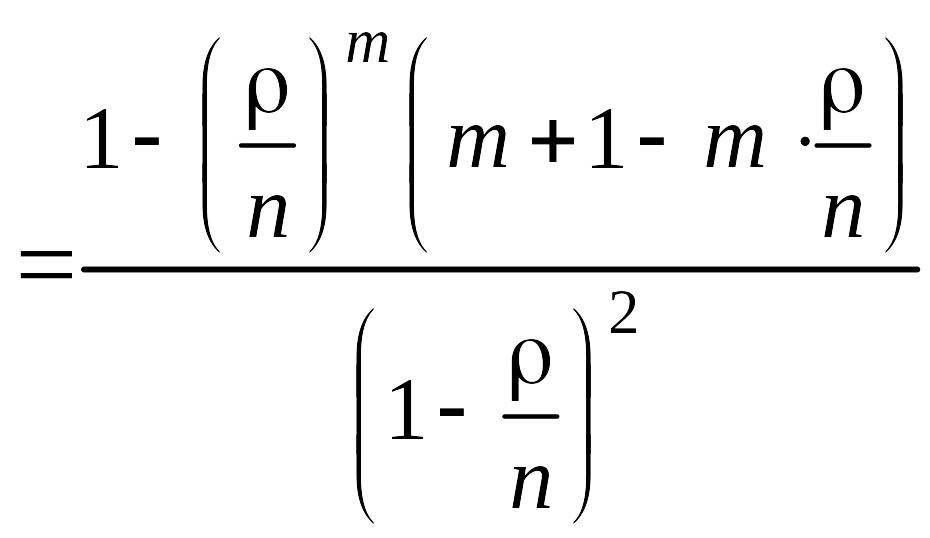. (5.4.8)

Заменив выражение в скобках в (5.4.7) на (5.4.8) будем иметь длину очереди при :

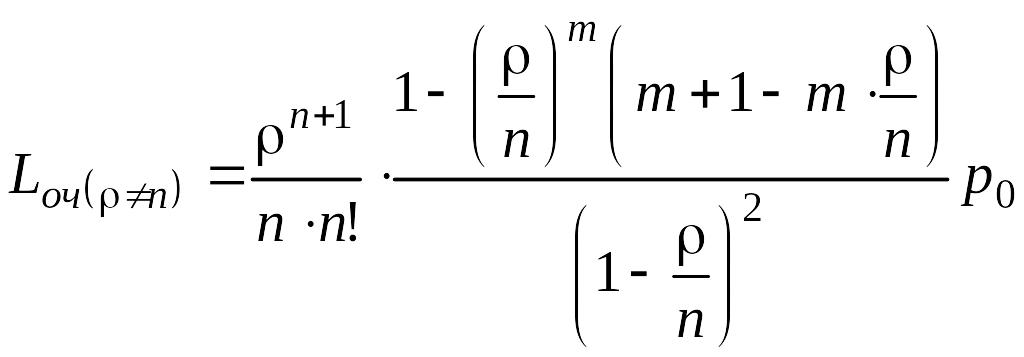. (5.4.9)

Длина очереди при получается непосредственно из (5.4.7)

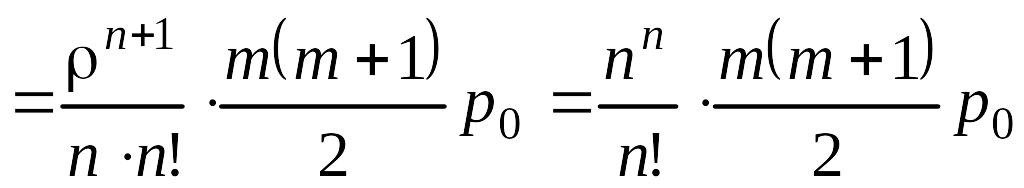. (5.4.10)

Итак, рассмотрен случай многоканальной СМО с ограниченной длиной очереди. Его выводы могут быть использованы для рассмотрения целого ряд других частных случаев.

Одноканальная СМО с ограниченной очередью (n = 1; 0< m < )

Из (5.4.3) при   1 имеем

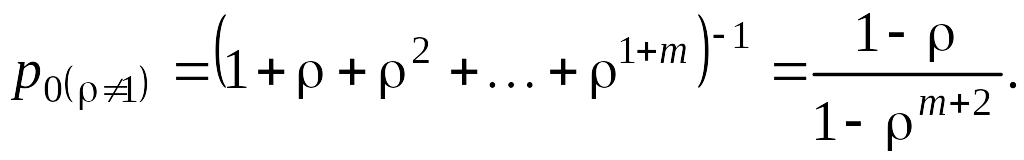(5.4.11)

При  = 1 имеем

(5.4.12)

Из (5.4.9) при   1 имеем

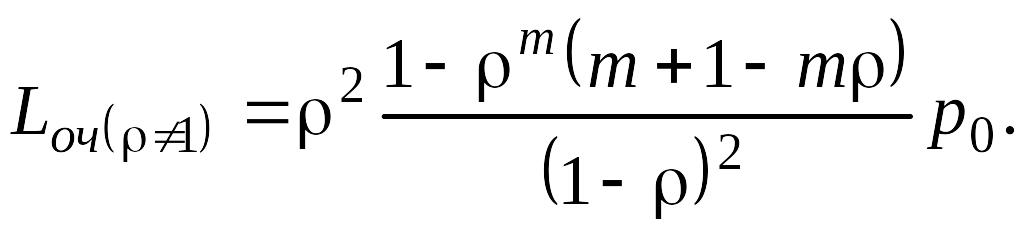
Из (5.4.10) и (5.4.12) при  = 1 имеем

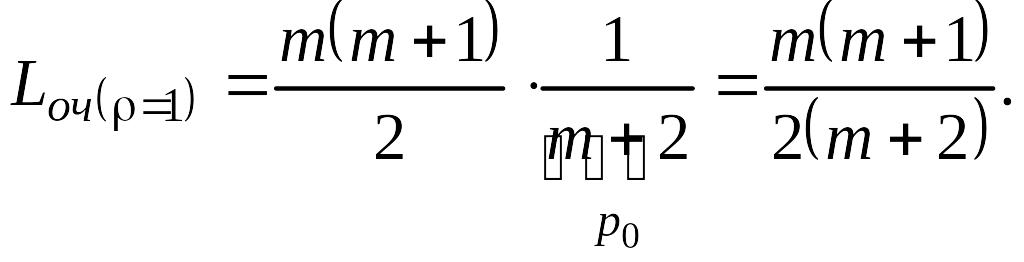
Из (5.4.6) и (5.4.11) получаем вероятность отказа в обслуживании при   1:

.

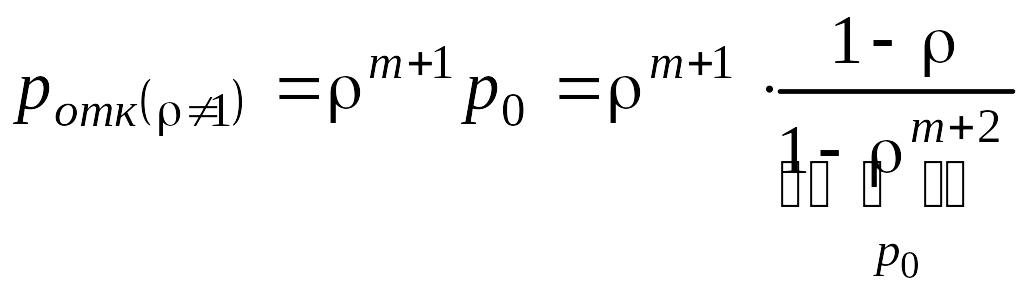Из (5.4.6) и (5.4.12) получаем вероятность отказа в обслуживании при  = 1:

.

Одноканальная СМО с неограниченной очередью (n = 1; m  )

Хотя она так называется, интерес имеют лишь устойчивые СМО, т.е. при  <  (что эквивалентно  < 1), в противном случае очередь неограниченно возрастает.

Естественно, что в данной СМО отказа быть не может, что непосредственно следует из (5.4.6), которая при  < 1 дает .

Из (5.4.3) имеем

.

Длину очереди получаем из (5.4.9) с использованием только что выведенной формулы для :

.