5.8. Модель авторегрессии 2-го порядка - ар(2)

Из авторегрессионных процессов выше 1-го порядка в экономиче­ской практике часто встречаются процессы 2-го порядка АР(2) (процессы Юла). Модель АР(2) может быть описана выражением:

. (5.8.1)

Умножим (5.8.1) на и :

(5.8.2)

Возьмем теперь математическое ожидание от обеих частей, при этом мы учтем, что

и . (5.8.3)

Действительно,

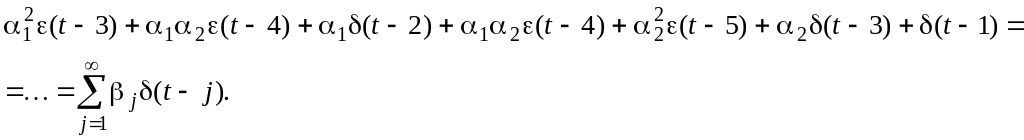
Поэтому . В соответствии со свойством (5.1.2) каждое из слагаемых равно 0. Следовательно, из сис­темы (5.8.2) имеем:

а после деления на :

(5.8.4)

Из (5.8.4) легко получим:

(5.8.5)

а также

. (5.8.6)

Умножив значение (5.8.1) на и беря математическое ожидание от обеих частей, а затем деля на , получим:

, (5.8.7)

что наряду с (5.8.6) позволяет полностью определить АКФ.

Теперь умножим (5.8.1) на :

.

Беря математическое ожидание от обеих частей и учитывая (5.8.3), полу­чим:

,

откуда

. (5.8.8)

Преобразуем в (5.8.8) выражение в фигурных скобках с учетом (5.8.6):

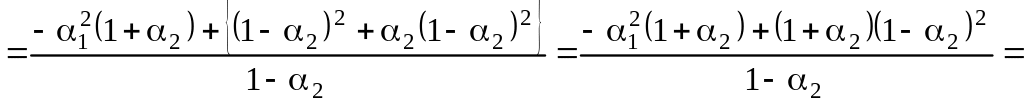
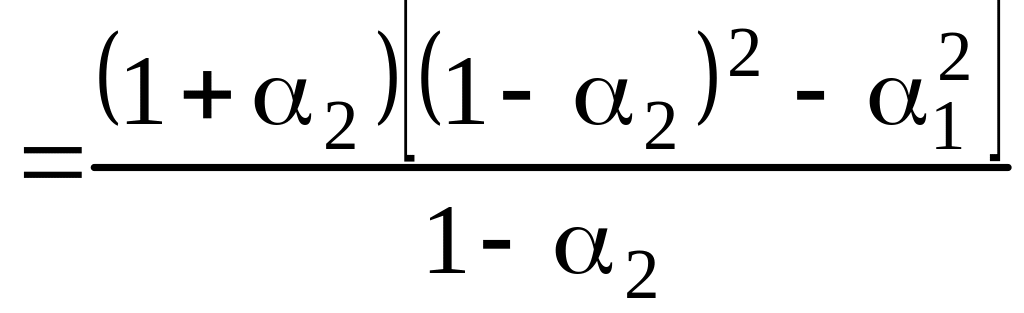. (5.8.9)

С учетом (5.8.9) и того, что , формулу (5.8.8) можно пере­писать так:

. (5.8.10)

ЧАКФ АР(2) можно найти по формулам (5.5.1-5.5.4) и с учетом (5.8.6):

, (5.8.11)

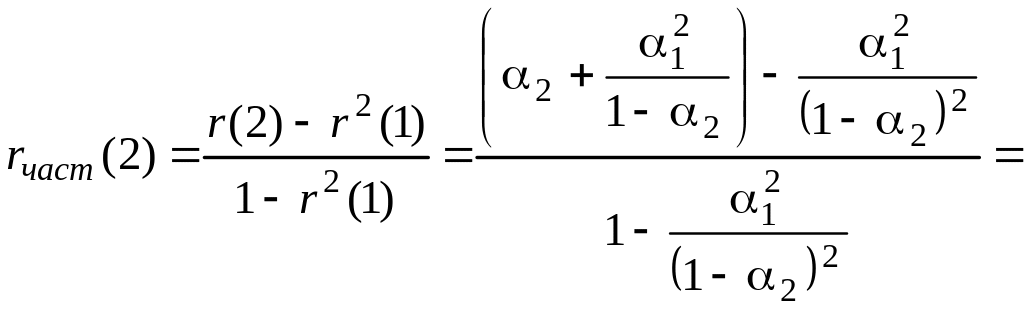
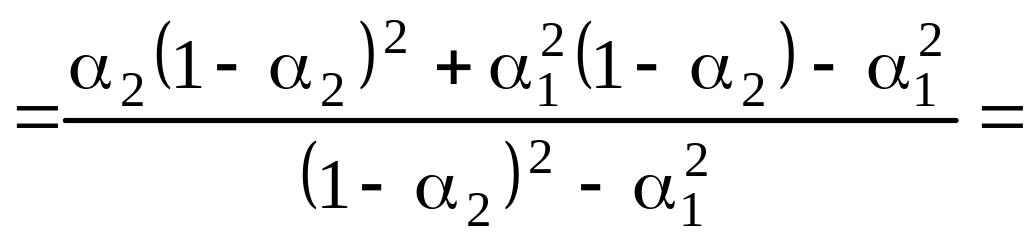
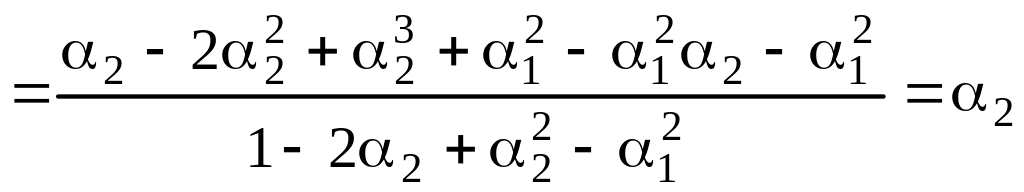. (5.8.12)

Для нахождения вначале найдем по рекуррентной форму­ле (5.8.7):

,

, (5.8.13)

так как числитель выражения (5.8.13) равен нулю.

Действительно, рассмотрим числитель (5.8.13):

(5.8.14)

Преобразуем теперь числитель выражения (5.8.14):

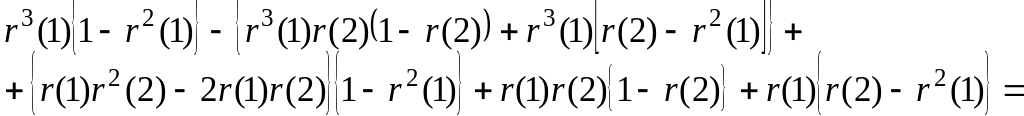
Вообще, можно показать, что и для .

Идентификация модели может быть построена на соотношениях (5.8.6),(5.8.7),(5.8.11)-(5.8.13). См. табл. 5.13.1.

Характеристическое уравнение (5.3.10) для данной модели запи­шется так:

. (5.8.15)

Из решения характеристического уравнения можно получить условия стационарности:

. (5.8.16)

Спектральная плотность может быть получена из общей формулы (5.6.8). Обозначив через , преобразуем знаменатель (5.6.8):

.

Тогда

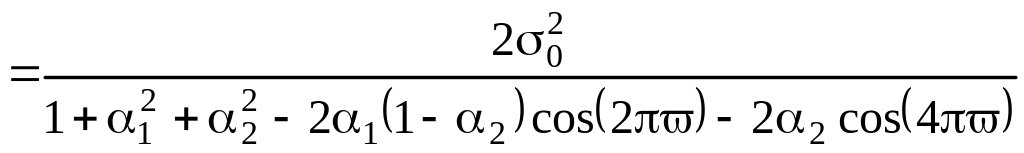, (5.8.17)

где определяется выражением (5.8.10).

Пример 5.8.1

Построить модель по данным, представленным в табл. 5.8.1. Сделать прогноз на 10 лет вперед. Расчеты выполнить в STATISTICA

Таблица 5.8.1. Динамика объемов ВВП США

(в ценах 1987 г., млрд.$ США) (23, с. 303)

Год	N п/п	Показатель	Год	N п/п	Показатель	Год	N п/п	Показатель
1959	1	1931.3	1970	12	2875.8	1981	23	3843.1
1960	2	1973.2	1971	13	2965.1	1982	24	3760.3
1961	3	2025.6	1972	14	3107.1	1983	25	3906.6
1962	4	2129.8	1973	15	3268.5	1984	26	4148.5
1963	5	2218	1974	16	3248.1	1985	27	4279.8
1964	6	2343.3	1975	17	3221.7	1986	28	4404.5
1965	7	2473.5	1976	18	3380.8	1987	29	4540
1966	8	2622.3	1977	19	3533.2	1988	30	4781.6
1967	9	2690.3	1978	20	3703.5	1989	31	4836.9
1968	10	2801	1979	21	3796.8	1990	32	4884.9
1969	11	2877.1	1980	22	3776.3	1991	33	4848.4

Решение

В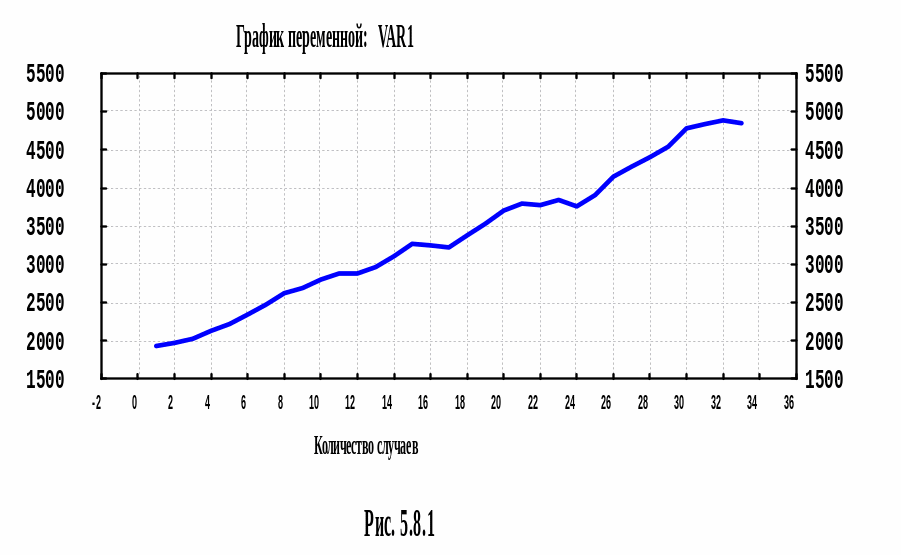 ыберем режим Advanced Linear/ Nonli-near Models, а в нем –подрежим Time Series Analysis – Анализ временных рядов и про­гнозирование. Появля-ется панель Time Series Analysis. На вкладке Quick нажмем на кнопку ARIMA&autokorrelation function – АРПСС и автокорреляционные функции и попадаем на панель Single Series ARIMA – одиночный временной ряд АРПСС. Выберем вкладку Review Series – просмотр временного ряда и нажмем на кнопку Plot – график.

Г рафик, полученный из данного временного ряда, очевидно, имеет тенденцию к возрастанию, которую можно аппроксимировать линейным трендом. После этого мы можем надеяться, что получим стационарный временной ряд. Для нахождения уравнения линейного тренда вернемся в режим Single Series ARIMA на вкладку Advanced, где нажмем на кнопку Other transformations&Plots и войдем в режим Transformations of Vari­ables - модификация переменных. На появившейся панели с одноименным названием переключим радиопереключатель на положение Trend Subtract – вычесть тренд и нажмем на кнопку OK (transform selected series). Будут вычислены параметры тренда . В списке переменных появится новая переменная с тем же Name – именем VAR1, но с отличным Long variable (series) name: . Закроем панель Transformations of Variables и вернемся на панель Single Series ARIMA. На ней выберем вкладку Autocorrelations и, нажимая последовательно на кнопки Autocorrelations и Partial Autocorrelations, получим значения АКФ и ЧАКФ. Мы видим, что ЧАКФ имеет выбросы на сдвигах 1 и 2. АКФ экспоненциально затухает. Следовательно, процесс может быть описан моделью АР(2). Вернемся снова на па­нель Single Series ARIMA. Перейдем на вкладку Advanced и установим параметр p-Autoregressive в 2. Затем нажмем на кнопку OK (Begin pa­rameter estimation), после чего начнется расчет параметра АР(2) модели и будет выдан результат, автоматически при этом произойдет смена закладки на закладку Review&residuals – анализ остатков. Но мы вернемся все же на вкладку Advanced, чтобы детальнее ознакомиться с результатами расчета. Нажимая на кнопку Summary:Parameter esti­mates, мы получим следующий результат:

p(1)= 0.982418 и p(2)= -0.453474 при p<0.05, следовательно, модель значима.

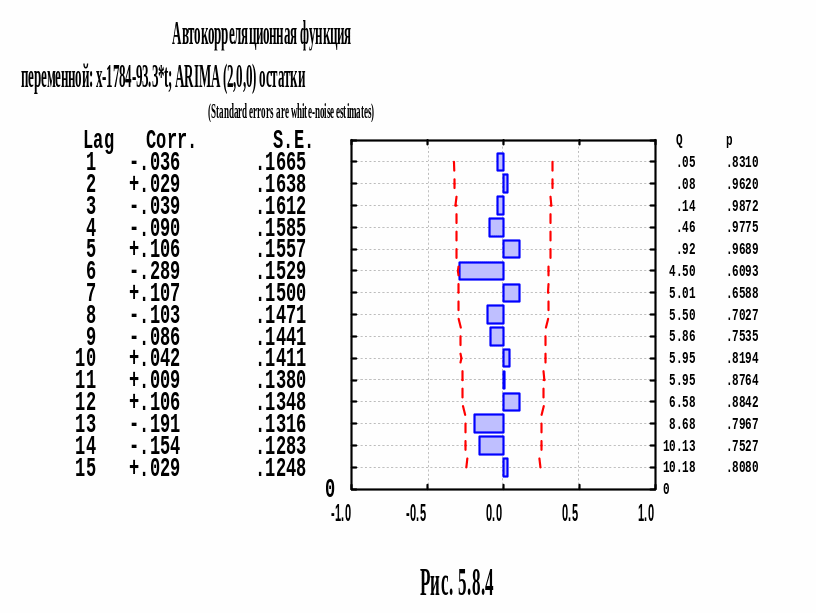
Теперь можно начать и непосредственно прогнозировать. Нажмем на кнопку Forecast cases. Получим прогнозные значения для следующих за 33-м моментом времени. По умолчанию прогноз выполняется для 10 следующих моментов времени, но этот параметр может быть изменен. Прогноз выполнен только для переменной, которая получена после удаления тренда. Чтобы дать реальные значения прогноза, необходимо к этим прогнозным значениям добавить прогноз по тренду. При этом расчетные значения тренда выполняются для моментов времени от 34-го до 43-го.

Можно также получить аналитическое представление модели. Нижеследующие выкладки эквивалентны тем, что мы выполняли, когда решали пример 5.7.1 в Excel:

По последнему уравнению делаем прогноз.

Таблица 5.8.2. Прогнозные значения показателя с 1992 по 2001 гг.

Год	N п/п	Показатель	Год	N п/п	Показатель
1992	34	4889.1	1997	39	5433.3
1993	35	4989.6	1998	40	5520.9
1994	36	5113.8	1999	41	5608.6
1995	37	5234.1	2000	42	5699.0
1996	38	5339.9	2001	43	5791.9

Насколько адекватна полученная модель реальности, мы судим по по­лученным остаткам модели. Поэтому зайдем на вкладку Autocorrelation и нажмем кнопку с таким же названием. Увидим, что АКФ ошибок находит­ся в доверительном интервале. Выберем вкладку Distribution of residuals и построим гистограмму ошибок. Видно, что распределение ошибок доста­точно хорошо подчиняется нормальному закону. Значит, результатам про­гноза можно доверять.