
- •Модель авторегрессии 1-го порядка - ар(1)
- •Продолжение табл. 5.7.2
- •5.8. Модель авторегрессии 2-го порядка - ар(2)
- •Теория очередей
- •Линейная сглаживающая функция
- •2.2. Параболическая и кубическая сглаживающие функции
- •Аналитическое выравнивание временных рядов
- •. Кривые роста и интерполирование
- •Кривые роста 1-го класса
- •1. Класс полиномов
- •2. Простая экспоненциальная (показательная) кривая
- •3. Логарифмическая парабола
- •Кривые роста 2-го класса
- •1. Модифицированная экспонента
- •§2.1. Аддитивная и мультипликативная модели
- •Классическая сезонная декомпозиция
- •§2.3. Проведение классической сезонной декомпозиции
- •Автокорреляционная функция (акф)
- •5.5. Частная автокорреляционная функция (чакф)
- •Финансовые решения в условиях риска
- •5.1. Динамические модели планирования финансов
Регулярные цепи Маркова
Матрица
переходных вероятностей называется
регулярной, если при некотором n
все элементы матрицы
![]() отличны от 0.
отличны от 0.
Теорема 4.2.1
Пусть
![]() – переходная матрица, не содержащая
нулевых элементов, и e
– наименьший элемент P.
Пусть
– переходная матрица, не содержащая
нулевых элементов, и e
– наименьший элемент P.
Пусть
![]() – один из столбцов матрицы P,
имеющий максимальную компоненту
– один из столбцов матрицы P,
имеющий максимальную компоненту
![]() и минимальную компоненту
и минимальную компоненту
![]() (имеется в виду для данного вектора), и
пусть
(имеется в виду для данного вектора), и
пусть
![]() и
и
![]() соответственно –максимальная и
минимальная компоненты вектора PX.
Тогда
соответственно –максимальная и
минимальная компоненты вектора PX.
Тогда
![]() и
и
![]() .
.
Доказательство
Образуем
вектор
![]() ,
элементами которого будут
и
,
элементами которого будут
и
![]() величин
.
Пусть, например, вектор X
представляет собой 1-й столбец матрицы
Р,
и его наименьшим элементом будет
величин
.
Пусть, например, вектор X
представляет собой 1-й столбец матрицы
Р,
и его наименьшим элементом будет
![]() .
Тогда соотношение между векторами X
и Y
будет таким:
.
Тогда соотношение между векторами X
и Y
будет таким:
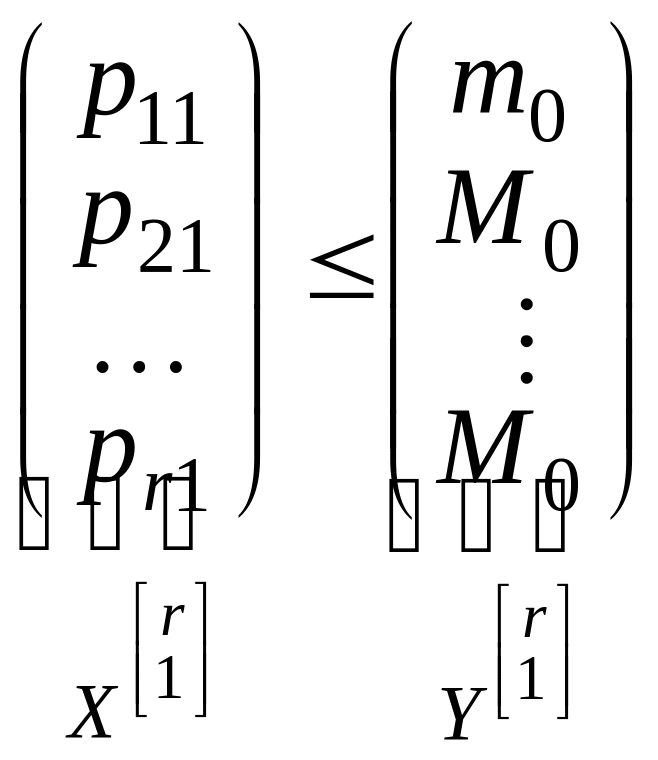 . (4.2.1)
. (4.2.1)
Далее запишем произведение PX и оценим его, используя (4.2.1):
![]()
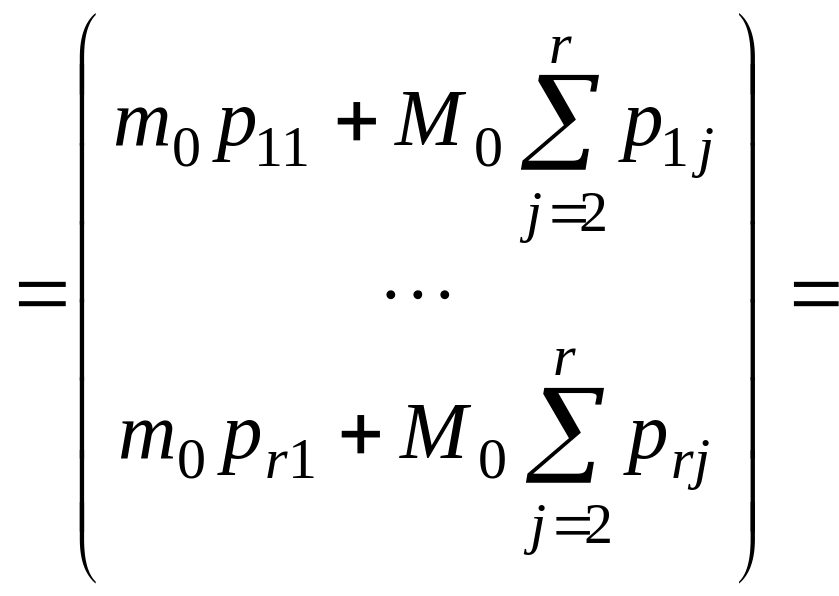
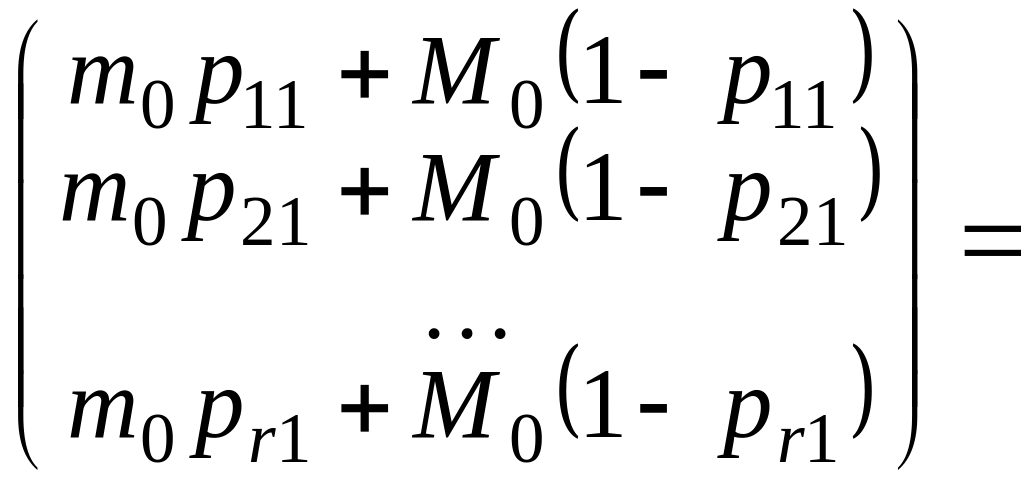
 . (4.2.2)
. (4.2.2)
Таким образом, в соответствии с соотношением (4.2.2) имеем
![]() . (4.2.3)
. (4.2.3)
Из
(4.2.3) при
![]() и
и
![]() следует
следует
![]() ,
что и требовалось
доказать.
,
что и требовалось
доказать.
Применим
этот же подход к вектору
![]() .
Но в этом случае для вектора
наибольшим элементом будет
.
Но в этом случае для вектора
наибольшим элементом будет
![]() ,
а наименьшим элементом будет
,
а наименьшим элементом будет
![]() .
Аналогично для вектора
.
Аналогично для вектора
![]() наибольшим элементом будет
наибольшим элементом будет
![]() ,
а наименьшим элементом будет
,
а наименьшим элементом будет
![]() .
.
![]()


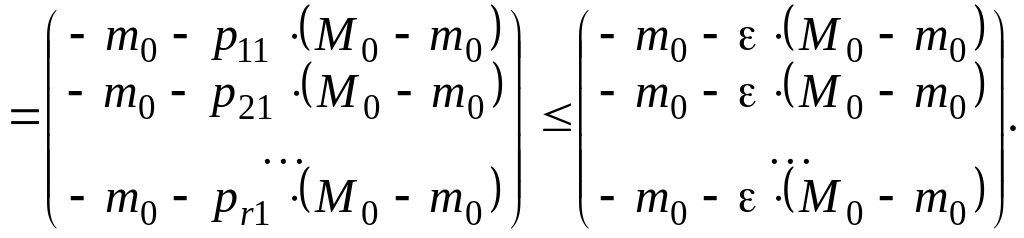 (4.2.4)
(4.2.4)
Таким образом, в соответствии с соотношением (4.2.4) имеем:
![]() . (4.2.5)
. (4.2.5)
Из
(4.2.5) при
и
следует
![]() ,
что требовалось
доказать.
,
что требовалось
доказать.
Складывая (4.2.3) и (4.2.5), получаем
![]() , (4.2.6)
, (4.2.6)
что завершает доказательство.
Теорема 4.2.2 [16]
Если P – регулярная матрица, то
степени
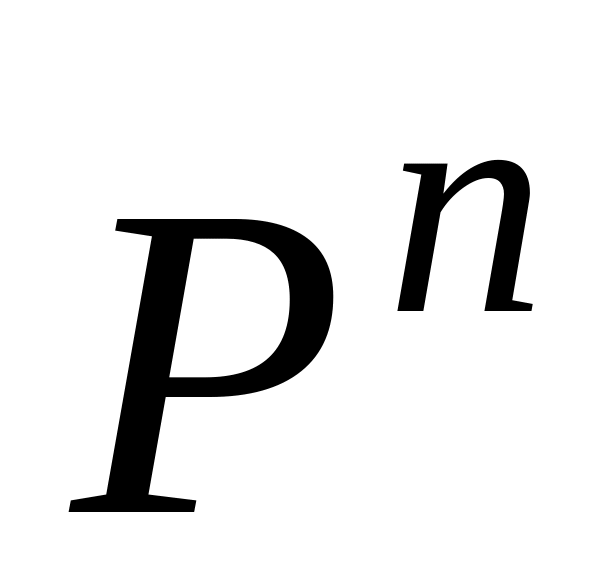 при
при
 стремятся
к так называемой вероятностной
матрице A;
стремятся
к так называемой вероятностной
матрице A;каждая из строк матрицы A представляет собой один и тот же вероятностный вектор , называемый также неподвижным
все компоненты вектора положительны.
![]() ;
;
Доказательство
Применим
теорему 4.2.1 к исходной матрице
с положительными элементами. То есть
будем брать последовательно каждый из
r
векторов
,
из которых эта матрица состоит, и
оценивать результативные столбцы PX.
Затем в качестве исходной будет
использоваться матрица P,
а в качестве векторов X
– столбцы матрицы![]() .
На третьем шаге в качестве исходной
будет использоваться все та же матрица
P,
а в качестве векторов X –
столбцы матрицы
.
На третьем шаге в качестве исходной
будет использоваться все та же матрица
P,
а в качестве векторов X –
столбцы матрицы
![]() и т. д. Наконец, на n-м
шаге в качестве исходной будет
использоваться все та же матрица P,
а в качестве векторов X –
столбцы матрицы
.
Так как для каждого из столбцов будем
иметь соотношения
и т. д. Наконец, на n-м
шаге в качестве исходной будет
использоваться все та же матрица P,
а в качестве векторов X –
столбцы матрицы
.
Так как для каждого из столбцов будем
иметь соотношения
![]() и
и
![]() ,
то для каждого столбца матрицы
значение максимального элемента будет
убывать, а значение минимального –
возрастать, при этом они будут оставаться
положительными. Записав последовательность
соотношений (4.2.6), получим
,
то для каждого столбца матрицы
значение максимального элемента будет
убывать, а значение минимального –
возрастать, при этом они будут оставаться
положительными. Записав последовательность
соотношений (4.2.6), получим
;
![]() ;
;
…
![]() при
при
![]() ,
,
что завершает доказательство.
Пример 4.2.1
Пример заимствован из [20, с. 168].
Для многих экономических задач необходимо знать чередование годов с определенными значениями годовых стоков рек. Введем четыре градации для стока:
1-я – самый низкий сток;
2-я
3-я
4-я – самый высокий сток.
В результате накопления влаги (в земле, водохранилищах и т.д.) будем считать, что за 1-й градацией никогда не следует 4-я, так же, как и за 4-й – 1-я.
На основе многолетних данных была составлена матрица переходных вероятностей
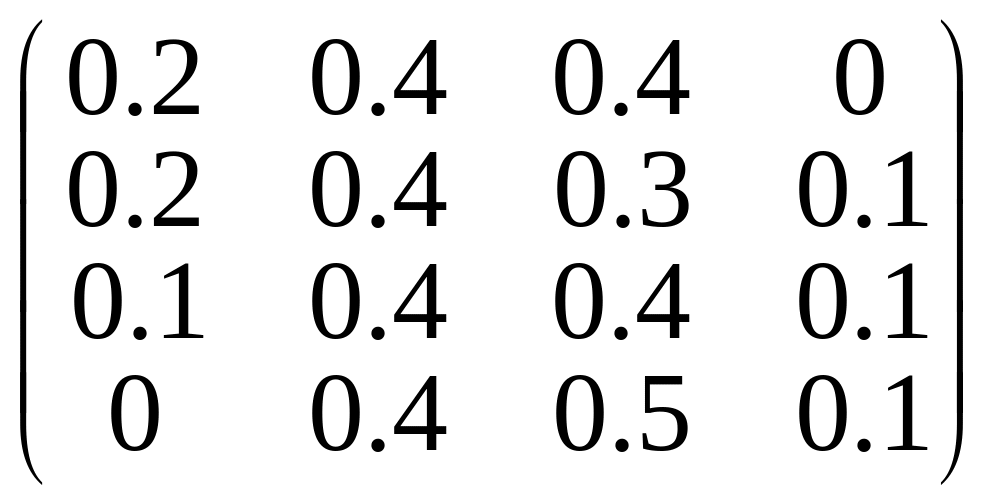 .
.
Убедиться, что данная матрица является регулярной. Установить периодичность засушливых и дождливых лет.
Решение в Excel
С
помощью программы 4.1.1 убеждаемся, что
уже
содержит только положительные элементы,
значит, она регулярна. Найдем предельное
распределение для цепи Маркова. Возведя
ее в 100-ю степень, получим вероятностную
матрицу А,
состоящую из одинаковых строк
![]() .
Итак, в среднем за 100 лет 14.6 лет будет
наблюдаться состояние 1, 40 лет – состояние
2, 36.8 лет – состояние 3 и 8.5 лет – состояние
4. Периодичность возвращения в i-е
состояние равна, следовательно, дроби
.
Итак, в среднем за 100 лет 14.6 лет будет
наблюдаться состояние 1, 40 лет – состояние
2, 36.8 лет – состояние 3 и 8.5 лет – состояние
4. Периодичность возвращения в i-е
состояние равна, следовательно, дроби
![]() .
Для
.
Для
![]() это составит 6.84, а для
это составит 6.84, а для
![]() – 11.7. Итак, периодичность засушливых
лет в среднем составляет 6–7 лет, а
дождливых – 12 лет.
– 11.7. Итак, периодичность засушливых
лет в среднем составляет 6–7 лет, а
дождливых – 12 лет.
Пример 4.2.3
Рассматривается динамика процесса изменения профессий по округу Мэрион штата Индиана. Имеются матрицы переходных вероятностей за 1910 г. и аналогичная матрица за 1940 г. (табл. 4.2.3). Профессии объединены в группы:
умственный труд;
физический труд;
труд, связанный с сельским хозяйством (фермеры).
Кроме того, имеются данные по распределению занятых по этим группам также за 1910 г. и 1940 г. Так, истинное распределение по профессиям:
1910 г.: 1) 0.1; 2) 0.658; 3) 0.034;
1940 г.: 1) 0.373; 2) 0.616; 3) 0.011.
Необходимо спрогнозировать, каково будет теоретическое распределение по профессиям через 30 лет в том и в другом случаях. Сравнить теоретическое распределение в 1-м случае с реальным.
Т а б л и ц а 4.2.3
|
A |
B |
C |
D |
E |
F |
G |
4 |
1910 год |
|
|
|
1940 год |
|
|
5 |
0.594 |
0.397 |
0.009 |
|
0.622 |
0.375 |
0.003 |
6 |
0.211 |
0.782 |
0.007 |
|
0.274 |
0.721 |
0.005 |
7 |
0.251 |
0.641 |
0.108 |
|
0.264 |
0.694 |
0.042 |
Решение в Excel
Возведя матрицы в 30-ю степень с помощью программы 4.1.1, получим следующий результат. В обоих случаях имеем неподвижные векторы, показывающие теоретическое распределение занятых по заданным группам профессий.
Т а б л и ц а 4.2.4
|
A |
B |
C |
D |
E |
F |
G |
9 |
Матрицы в степени 30 |
||||||
10 |
0.342532 |
0.64892 |
0.008548 |
|
0.4201791 |
0.575501 |
0.004319 |
11 |
0.342532 |
0.64892 |
0.008548 |
|
0.4201791 |
0.575501 |
0.004319 |
12 |
0.342532 |
0.64892 |
0.008548 |
|
0.4201791 |
0.575501 |
0.004319 |
13 |
Фактическое распределение |
|
|
|
|
||
14 |
0.373 |
0.616 |
0.011 |
|
|
|
|
Из табл. 4.2.4 заключаем, что фактическое распределение 1940 г. несколько отличается от предсказанного по данным 1910 г с помощью теории дискретных марковских цепей. Налицо увеличение доли лиц умственного труда, что отражает влияние технического прогресса. Таким образом, с помощью однородных марковских цепей осуществляется экстраполирование наметившихся тенденций в будущее, так как матрица переходных вероятностей не меняется.
Поглощающие цепи Маркова
Рассмотрение данного вида марковских цепей начнем с примера, которым было начато рассмотрение цепей Маркова.
Пример 4.4.1
Множество состояний студентов некоторого вуза с 5-летним сроком обучения:
лица, обучавшиеся в вузе, но не закончившие его;
специалисты, окончившие вуз;
выпускник;
четверокурсник;
третьекурсник;
второкурсник;
первокурсник.
Матрица переходных вероятностей P, составленная на основе многолетней информации, представлена в табл. 4.4.1 Excel. Из нее можно сделать вывод, что она не является регулярной хотя бы потому, что ячейки B3:C4 представляют собой единичную подматрицу. Следовательно, природа данной матрицы переходных вероятностей отлична от изученных нами регулярных матриц. Получить предельную матрицу.
Т а б л и ц а 4.4.1
|
A |
B |
C |
D |
E |
F |
G |
H |
2 |
|
1-е сост. |
2-е сост. |
3-е сост. |
4-е сост. |
5-е сост. |
6-е сост. |
7-е сост. |
3 |
1-е состояние |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
2-е состояние |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
5 |
3-е состояние |
0.05 |
0.9 |
0.05 |
0 |
0 |
0 |
0 |
6 |
4-е состояние |
0.1 |
0 |
0.85 |
0.05 |
0 |
0 |
0 |
7 |
5-е состояние |
0.1 |
0 |
0 |
0.8 |
0.1 |
0 |
0 |
8 |
6-е состояние |
0.15 |
0 |
0 |
0 |
0.7 |
0.15 |
0 |
9 |
7-е состояние |
0.2 |
0 |
0 |
0 |
0 |
0.7 |
0.1 |
Решение в Excel
Возведя матрицу в 100-ю степень с помощью программы, получим следующий результат:
Т а б л и ц а 4.4.2
|
A |
B |
C |
D |
E |
F |
G |
H |
2 |
|
1-е сост. |
2-е сост. |
3-е сост. |
4-е сост. |
5-е сост. |
6-е сост. |
7-е сост. |
3 |
1-е состояние |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
2-е состояние |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
5 |
3-е состояние |
0.052632 |
0.947368 |
7.9E-131 |
0 |
0 |
0 |
0 |
6 |
4-е состояние |
0.152355 |
0.847645 |
1.3E-127 |
7.9E-131 |
0 |
0 |
0 |
7 |
5-е состояние |
0.246537 |
0.753463 |
2.72E-98 |
1.6E-99 |
1E-100 |
0 |
0 |
8 |
6-е состояние |
0.379501 |
0.620499 |
3.87E-80 |
4.55E-81 |
5.69E-82 |
4.07E-83 |
0 |
9 |
7-е состояние |
0.51739 |
0.48261 |
5.42E-79 |
6.37E-80 |
7.97E-81 |
5.69E-82 |
1E-100 |
Из табл. 4.4.2 следует, что поступивший в институт либо его покинет, не закончив, либо окончит и получит диплом. Следовательно, в данном примере имеются два состояния, в которые данный процесс ведет. Очевидно, что если рассматривать данный процесс в течение длительного времени, то нахождение в любом другом состоянии (в процессе обучения, т.е. в состояниях с 3-го по 7-е) представляется очень мало вероятным, о чем свидетельствуют вероятности в ячейках табл. 4.4.2 D5:H9. Итак, первокурсник в данном вузе (состояние 7) лишь с вероятностью 48.2% окончит вуз с дипломом и с вероятностью 51.7% не закончит его. Шансы окончить институт по мере увеличения курса обучения неуклонно возрастают, приближаясь к 94.7%, если студент переведен на 5-й курс.
Очевидно, что состояния, присутствующие в матрице P переходных вероятностей различаются. Возведение ее в 100-ю степень показывает, что имеются два предельных состояния, к которым стремится процесс. Эти состояния получили название поглощающих. Попав в эти состояния, из них уже не выйти. Состояния с 3-го по 7-е представляют собой соответственно 5-й, 4-й, 3-й, 2-й и 1-й курс обучения. Большинство студентов будут их последовательно проходить начиная с 1-го по 5-й курс. Эти состояния получили название транзитивных. В данном случае имеется 2 поглощающих и 5 транзитивных состояний. Поглощающими называются цепи, в которых существуют поглощающие состояния, вероятность остаться в которых равна 1 и транзитивные, с помощью которых можно попасть в поглощающие. Например, матрица
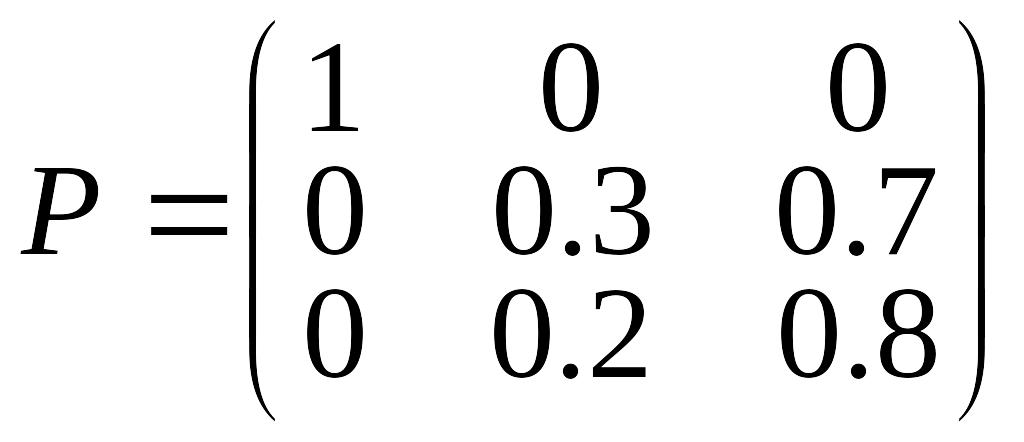
не является поглощающей, так как в состояние 1 перехода нет.
Внимательный читатель, несомненно, заметил, что те состояния, которые используются в примере 4.4.1, несколько искусственны, так как логичнее было бы нумеровать их в обратном порядке. Однако они пронумерованы так сознательно, чтобы прийти к описанию общей теории, к которой сейчас и приступаем.
В общем случае, пусть имеется некоторая матрица переходных вероятностей P, состояния которой можно пронумеровать так, чтобы образовать в матрице в левой верхней части единичную подматрицу. Тогда матрицу P можно записать следующим образом:
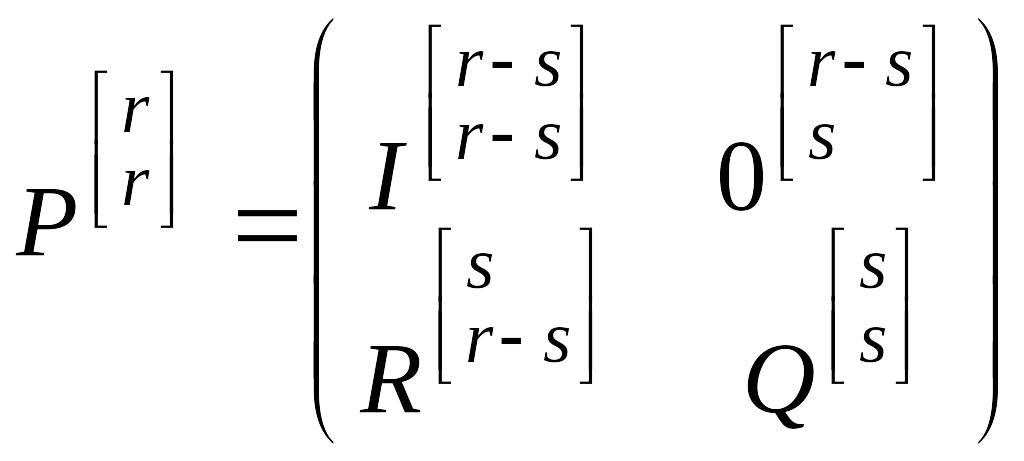 , (4.4.1)
, (4.4.1)
где
![]() – единичная
матрица;
– единичная
матрица;
![]() – нулевая
матрица;
– нулевая
матрица;
![]() – матрица
перехода между транзитивными и
поглощающими состояниями;
– матрица
перехода между транзитивными и
поглощающими состояниями;
![]() – матрица
вероятностей перехода между транзитивными
состояниями.
– матрица
вероятностей перехода между транзитивными
состояниями.
Как
было показано в примере 4.4.1, где матрица
P
имела подобную структуру, в пределе при
![]() матрица
матрица
![]()
 , (4.4.2)
, (4.4.2)
где матрица B представляет собой матрицу вероятностей перехода к поглощающим состояниям. В компьютерную эпоху ее можно вычислить путем возведения матрицы P в достаточно большую степень, что представляло сложность во времена Маркова. Однако теория даст нам возможность не только получить матрицу В без возведения матриц в степень, но и ответить на множество других вопросов.
Первый из этих вопросов очевиден. Поскольку независимо от начального состояния элемент, в конце концов, попадет в одно из поглощающих, то хотелось бы знать, как долго будет осуществляться переход от одного транзитивного состояния к другому до момента, когда он попадет в поглощающее состояние.
Итак,
пусть матрица
![]() представляет собой матрицу средних
продолжительностей пребывания в каждом
из транзитивных состояний, т.е.
до поглощения.
Элементы
представляет собой матрицу средних
продолжительностей пребывания в каждом
из транзитивных состояний, т.е.
до поглощения.
Элементы
![]() до начала процесса равны величине
до начала процесса равны величине
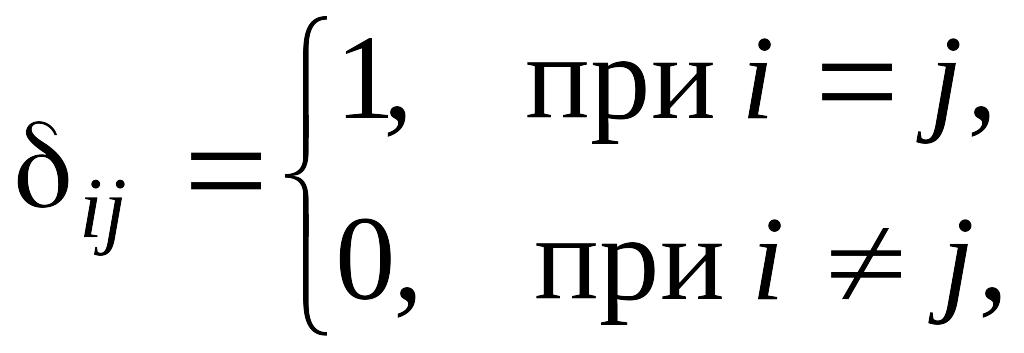
затем
на 1-м шаге процесса к ним добавляются
элементы
![]() матрицы Q,
на 2-м шаге – добавится значение
матрицы Q,
на 2-м шаге – добавится значение
![]() и т.д. Или в матричной форме:
и т.д. Или в матричной форме:
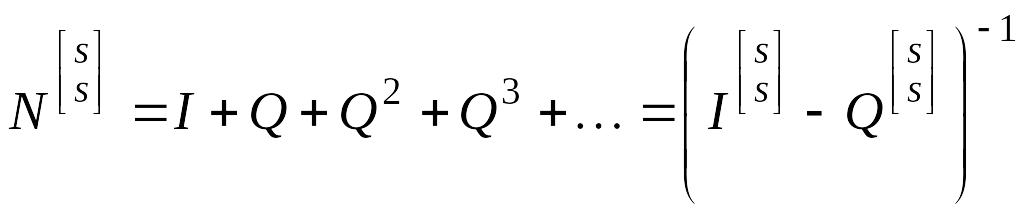 , (4.4.3)
, (4.4.3)
так как если обе части равенства
![]()
умножить
на
![]() ,
то в правой части будем иметь I,
а в левой
,
то в правой части будем иметь I,
а в левой
![]() ,
,
т.е. тоже I. Матрица N, выражаемая (4.4.3) называется фундаментальной матрицей для поглощающих цепей.
К
(4.4.3) можно прийти и с помощью такого
рассуждения. Величина
складывается из
![]() и суммы по транзитивным состояниям
и суммы по транзитивным состояниям
![]() ,
,
или в матричном виде
![]() .
.
Если нужно узнать, сколько всего времени элемент будет находиться в транзитивных состояниях, если процесс начинается с i-го транзитивного состояния, надо просуммировать значения i-й строки фундаментальной матрицы. Обозначим ее буквой m. Иными словами, для получения вектора значений m по всем s исходным транзитивным состояниям достаточно умножить фундаментальную матрицу на столбец из единиц:
![]() . (4.4.4)
. (4.4.4)
С
помощью фундаментальной матрицы (4.4.3)
могут быть найдены вероятности перехода
к поглощающим состояниям, т.е. матрица
![]() .
Действительно, пусть индексы i
и
k
относятся к транзитивным состояниям,
а j
– к поглощающим. Тогда
.
Действительно, пусть индексы i
и
k
относятся к транзитивным состояниям,
а j
– к поглощающим. Тогда
![]() ,
,
где
величина
![]() представляет собой вероятность прямого
перехода из транзитивного в поглощающее
состояние, а второй член добавляет к
ней вероятность непрямых переходов. В
матричном виде последнее соотношение
может быть записано в виде
представляет собой вероятность прямого
перехода из транзитивного в поглощающее
состояние, а второй член добавляет к
ней вероятность непрямых переходов. В
матричном виде последнее соотношение
может быть записано в виде
![]() ,
,
или
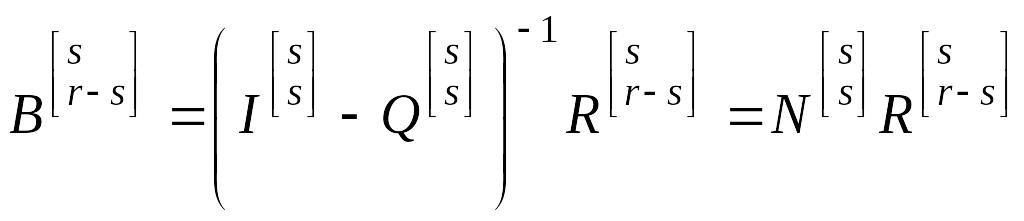 . (4.4.5)
. (4.4.5)
Пример 4.4.2
Используя данные примера 4.4.1, найти матрицы N, B.
Решение в Excel
Выделим
вначале матрицы
![]() ,
,
![]() и сформируем единичную матрицу размерности
5:
и сформируем единичную матрицу размерности
5:
матрица R располагается в табл. 4.4.3 в ячейках A21:B25: {=B5:C9};
матрица Q – в ячейках D27:H31: {=D5:H9};
матрица I размерностью 5 – в ячейках D21:H25.
Т а б л и ц а 4.4.3
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
20 |
Матрица R |
|
Матрица I |
Матрица 1 |
||||||
21 |
0.05 |
0.9 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
22 |
0.1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
1 |
23 |
0.1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
1 |
24 |
0.15 |
0 |
|
0 |
0 |
0 |
1 |
0 |
|
1 |
25 |
0.2 |
0 |
|
0 |
0 |
0 |
0 |
1 |
|
1 |
26 |
|
|
|
Матрица Q |
|
|
||||
27 |
|
|
|
0.05 |
0 |
0 |
0 |
0 |
|
|
28 |
|
|
|
0.85 |
0.05 |
0 |
0 |
0 |
|
|
29 |
|
|
|
0 |
0.8 |
0.1 |
0 |
0 |
|
|
30 |
|
|
|
0 |
0 |
0.7 |
0.15 |
0 |
|
|
31 |
|
|
|
0 |
0 |
0 |
0.7 |
0.1 |
|
|
Затем получим фундаментальную матрицу поглощающей цепи по (4.4.3). Расчеты представлены в табл. 4.4.4. Так, в ячейках D34:H38 записана формула {=D21:H25-D27:H31}, а в ячейках D41:H45 рассчитывается фундаментальная матрица поглощающей цепи по формуле {=МОБР(D34:H38)}.
Т а б л и ц а 4.4.4
|
D |
E |
F |
G |
H |
33 |
Матрица (I-Q) |
|
|
|
|
34 |
0.95 |
0 |
0 |
0 |
0 |
35 |
-0.85 |
0.95 |
0 |
0 |
0 |
36 |
0 |
-0.8 |
0.9 |
0 |
0 |
37 |
0 |
0 |
-0.7 |
0.85 |
0 |
38 |
0 |
0 |
0 |
-0.7 |
0.9 |
39 |
Фундаментальная матрица |
|
|
||
40 |
|
|
|
|
|
41 |
1.052632 |
0 |
0 |
0 |
0 |
42 |
0.941828 |
1.052632 |
0 |
0 |
0 |
43 |
0.837181 |
0.935673 |
1.111111 |
0 |
0 |
44 |
0.689443 |
0.770554 |
0.915033 |
1.176471 |
0 |
45 |
0.536233 |
0.59932 |
0.711692 |
0.915033 |
1.111111 |
Наконец,
рассчитываем средние значения времени
пребывания в институте, т.е. компоненты
вектора-столбца
![]() и вероятности перехода в поглощающее
состояние по формуле (4.4.5). Данные расчеты
представлены в табл. 4.4.5. Так, в ячейках
D49:D53
рассчитывается вектор m
по формуле {=МУМНОЖ(D41:H45;J21:J25)},
а в ячейках G49:H53
матрица B,
которая совпадает с аналогичной матрицей,
полученной ранее в табл. 4.4.2.
и вероятности перехода в поглощающее
состояние по формуле (4.4.5). Данные расчеты
представлены в табл. 4.4.5. Так, в ячейках
D49:D53
рассчитывается вектор m
по формуле {=МУМНОЖ(D41:H45;J21:J25)},
а в ячейках G49:H53
матрица B,
которая совпадает с аналогичной матрицей,
полученной ранее в табл. 4.4.2.
Т а б л и ц а 4.4.5
|
D |
E |
F |
G |
H |
48 |
m |
|
|
B=NR |
|
49 |
1.052632 |
|
|
0.052632 |
0.947368 |
50 |
1.99446 |
|
|
0.152355 |
0.847645 |
51 |
2.883964 |
|
|
0.246537 |
0.753463 |
52 |
3.5515 |
|
|
0.379501 |
0.620499 |
53 |
3.873389 |
|
|
0.51739 |
0.48261 |
Поясним числовые результаты табл. 4.4.5. Из матрицы B следует, что вероятность окончить вуз для поступившего на 1-й курс составляет 48.2%. Естественно эта вероятность при последовательном продвижении с курса на курс повышается, достигая на начало 5-го курса 94.7%. На время пребывания студента в вузе действует 2 фактора:
1) возможность остаться для повторного обучения, что действует в направлении увеличения времени пребывания в вузе;
2) возможность отчисления, что действует в направлении уменьшения этого времени.
На 1-м курсе в среднем студент будет учиться 3.87 года, так как вероятность отчисления велика, а именно 51.7% (т.е. почти столько же, сколько и студента 2-го курса). Ситуация подобна феномену новорожденного в странах с высокой младенческой смертностью, когда ожидаемая продолжительность жизни у новорожденных может быть меньше, чем у годовалых детей. Иная ситуация на 5-м курсе. Здесь студент в среднем будет учиться 1.05 года, так как вероятность отчисления составляет всего 5.26%.
Модель авторегрессии 1-го порядка - ар(1)
Рассмотрим простейший вариант линейного авторегрессионного процесса – модель АР(1), который также называют марковским процессом:
![]() .
(5.7.1)
.
(5.7.1)
Из
(5.7.1) следует
![]()
![]()
![]()
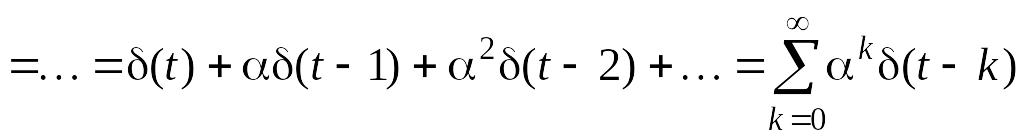 (5.7.2)
(5.7.2)
Из
(5.7.2), учитывая (5.1.1)
и (5.1.2), следует,
что
![]() ,
а
,
а
![]()
![]()
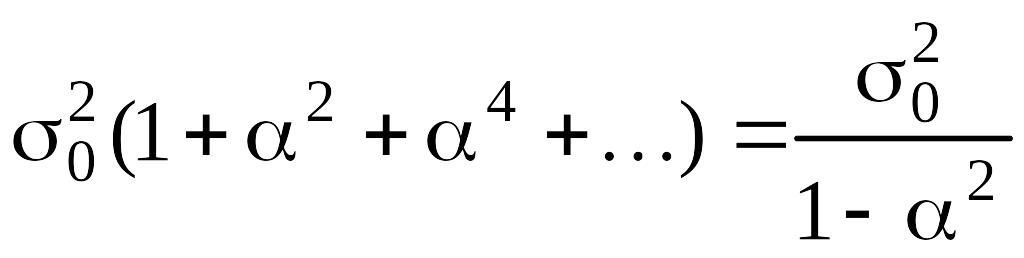 ,
,
т.е.
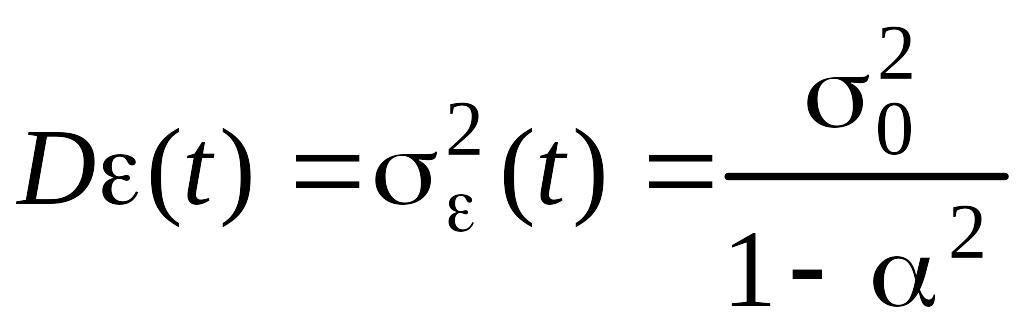 .
(5.7.3)
.
(5.7.3)
Для
вычисления ковариаций
![]() представим
представим
![]() с учетом соотношения (5.7.2)
в виде
с учетом соотношения (5.7.2)
в виде
![]()
![]() .
.
Тогда,
поскольку из взаимной некоррелированности
![]() следует взаимная некоррелированность
случайных величин
следует взаимная некоррелированность
случайных величин
![]() и
и
![]() ,
,
получаем:
![]()
![]()
![]() .
(5.7.4)
.
(5.7.4)
Разделив
соотношение (5.7.4) на
![]() ,
получим
,
получим
![]() ,
или
,
или
![]() .
(5.7.5)
.
(5.7.5)
АКФ полностью определяется поэтому соотношением (5.7.5). Отсюда, в частности, следует, что
![]() .
.
Характеристическое уравнение (5.3.10) для данной модели запишется так:
![]() .
(5.7.6)
.
(5.7.6)
Для
того, чтобы ряд в правой части (5.7.2)
сходился, необходимо, чтобы
![]() , откуда следует, что корень уравнения
(5.7.6)
, откуда следует, что корень уравнения
(5.7.6)
![]() должен быть по абсолютной величине
больше 1. Это также вытекает и из теории
разностных уравнений.
должен быть по абсолютной величине
больше 1. Это также вытекает и из теории
разностных уравнений.
ЧАКФ марковского процесса для k=1 и k=2 легко может быть найдена по формулам (5.5.1-5.5.4). Так,
![]() ,
(5.7.7)
,
(5.7.7)
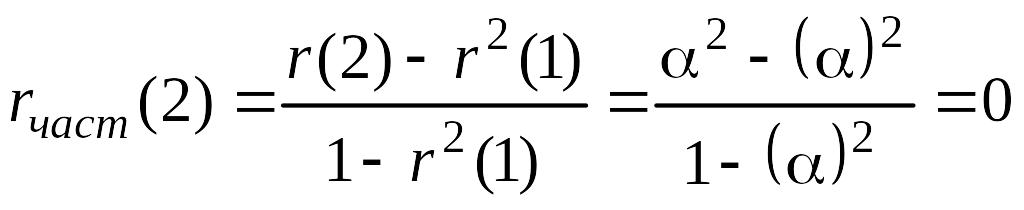 .
(5.7.8)
.
(5.7.8)
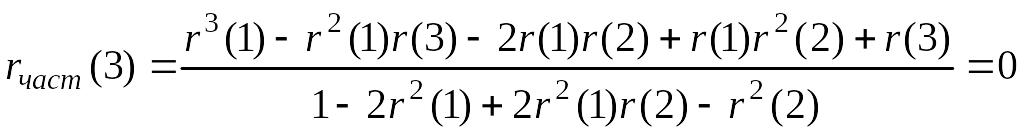 ,
(5.7.9)
,
(5.7.9)
так как числитель выражения (5.7.9) равен
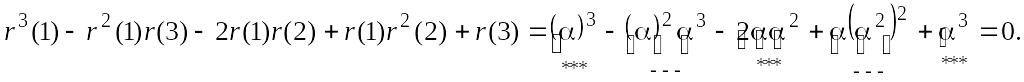 Вообще
можно показать, что и
Вообще
можно показать, что и
![]() для
для
![]() .
(5.7.10)
.
(5.7.10)
Спектральная
плотность
может быть получена из общей формулы
(5.6.8). Обозначив
через
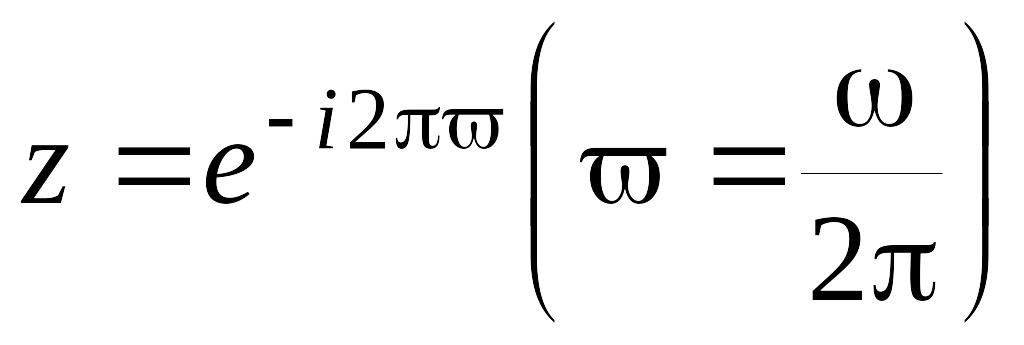 ,
имеем:
,
имеем:
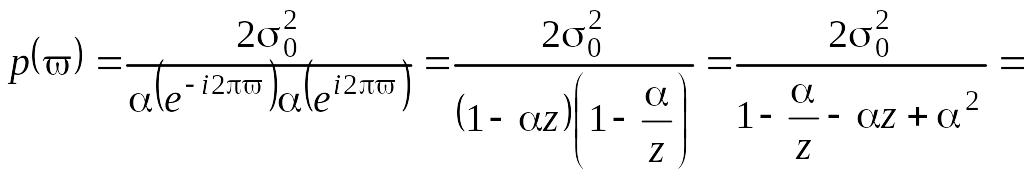
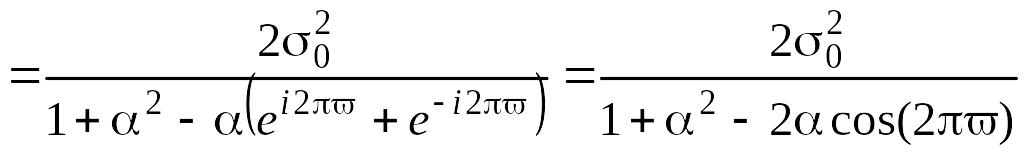 .
(5.7.11)
.
(5.7.11)
Учитывая
(5.7.3), выразим
![]() через
:
через
:
![]() .
Тогда окончательно будем иметь
практическую формулу для вычисления
спектральной плотности (так как дисперсию
.
Тогда окончательно будем иметь
практическую формулу для вычисления
спектральной плотности (так как дисперсию
![]() ряда найти легко):
ряда найти легко):
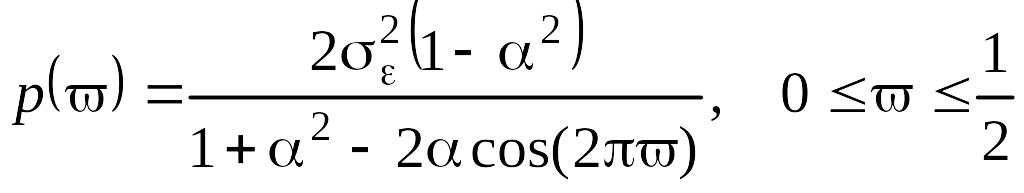 .
(5.7.12)
.
(5.7.12)
Идентификация модели может быть построена на соотношениях (5.7.5),(5.7.7) и (5.7.10). См. табл. 5.13.1.
Пример 5.7.1
Построить модель по данным, представленными в табл. 5.7.1. Сделать прогноз на 10 лет вперед. Расчеты выполнить в STATISTICA и в Excel.
Таблица 5.7.1 Динамика выработки цемента на 1 работающего (в т)
на Рижском цементном заводе с 1966 по 1986 гг (21, с. 111)
-
Год
N п/п
Показатель
Год
N п/п
Показатель
1966
1
673
1976
11
900
1967
2
694
1977
12
951
1968
3
711
1978
13
915
1969
4
786
1979
14
938
1970
5
797
1980
15
847
1971
6
782
1981
16
891
1972
7
810
1982
17
885
1973
8
832
1983
18
883
1974
9
834
1984
19
867
1975
10
878
1985
20
824
1986
21
918
Р ешение
в STATISTICA
ешение
в STATISTICA
Выберем режим Advanced Linear/Nonlinear Models, а в нем – подрежим Time Series Analysis – Анализ временных рядов и прогнозирование. Появляется панель Time Series Analysis. На вкладке Quick нажмем на
к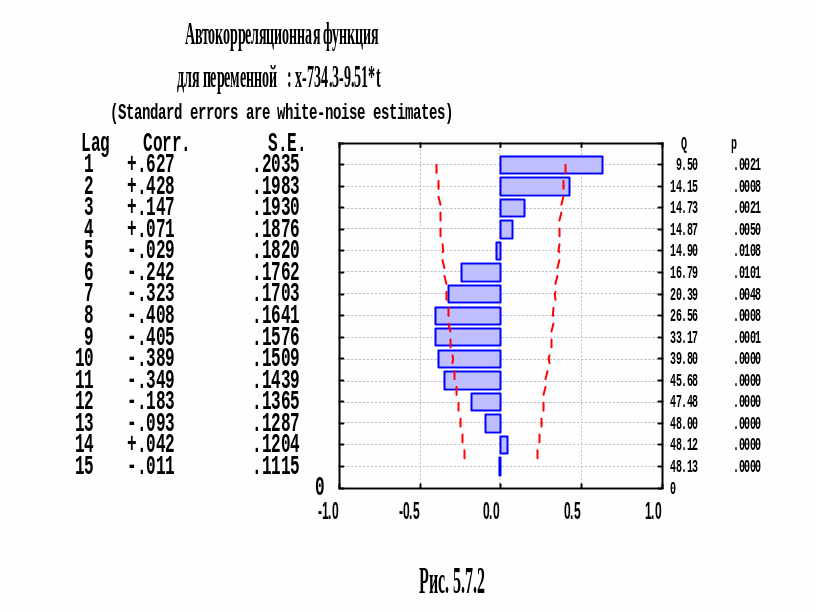 нопку
ARIMA&autokorrelation
function
– АРПСС и автокорреляционные функции
и попадаем
на панель
Single
Series
ARIMA
– одиночный временной ряд АРПСС. Выберем
вкладку Review
Series
– просмотр временного ряда и
нажмем на кнопку
Plot
– график.
График, полученный из данного временного
ряда, очевидно, имеет тенденцию к
возрастанию, которую можно аппроксимировать
линейным трендом. После этого мы можем
надеяться, что получим стационарный
временной ряд. Для нахождения уравнения
линейного тренда вернемся в режим Single
Series
ARIMA
на вкладку Advanced,
где нажмем на кнопку Other
transformations&Plots
и войдем в
режим
Transformations
of
Variables
- модификация
переменных.
На появившейся
панели с одноименным названием переключим
радиопереключатель на положение Trend
Subtract
– вычесть
тренд и нажмем на кнопку OK
(transform selected series). Будут
вычислены параметры тренда
нопку
ARIMA&autokorrelation
function
– АРПСС и автокорреляционные функции
и попадаем
на панель
Single
Series
ARIMA
– одиночный временной ряд АРПСС. Выберем
вкладку Review
Series
– просмотр временного ряда и
нажмем на кнопку
Plot
– график.
График, полученный из данного временного
ряда, очевидно, имеет тенденцию к
возрастанию, которую можно аппроксимировать
линейным трендом. После этого мы можем
надеяться, что получим стационарный
временной ряд. Для нахождения уравнения
линейного тренда вернемся в режим Single
Series
ARIMA
на вкладку Advanced,
где нажмем на кнопку Other
transformations&Plots
и войдем в
режим
Transformations
of
Variables
- модификация
переменных.
На появившейся
панели с одноименным названием переключим
радиопереключатель на положение Trend
Subtract
– вычесть
тренд и нажмем на кнопку OK
(transform selected series). Будут
вычислены параметры тренда
![]() .
В списке
переменных появится новая переменная
с тем же Name
- именем VAR1,
но с отличным
Long
variable
(series)
name:
.
В списке
переменных появится новая переменная
с тем же Name
- именем VAR1,
но с отличным
Long
variable
(series)
name:
![]() .
Закроем
панель
Transformations
of Variables и
вернемся
на
панель
Single Series ARIMA. На
ней выберем вкладку
Autocorrelations
и, нажимая
последовательно на кнопки Autocorrelations
и Partial
Autocorrelations,
получим значения АКФ (выборочной
автокорреляционной функции) и ЧАКФ
(выборочной частной автокорреляционной
функции). Мы видим, что ЧАКФ имеет выбросы
на сдвиге 1. АКФ экспоненциально затухает.
Следовательно, процесс
.
Закроем
панель
Transformations
of Variables и
вернемся
на
панель
Single Series ARIMA. На
ней выберем вкладку
Autocorrelations
и, нажимая
последовательно на кнопки Autocorrelations
и Partial
Autocorrelations,
получим значения АКФ (выборочной
автокорреляционной функции) и ЧАКФ
(выборочной частной автокорреляционной
функции). Мы видим, что ЧАКФ имеет выбросы
на сдвиге 1. АКФ экспоненциально затухает.
Следовательно, процесс
![]() может быть
описан моделью
АР(1). Вернемся
снова на
панель Single
Series
ARIMA.
Перейдем на вкладку Advanced
и устан
может быть
описан моделью
АР(1). Вернемся
снова на
панель Single
Series
ARIMA.
Перейдем на вкладку Advanced
и устан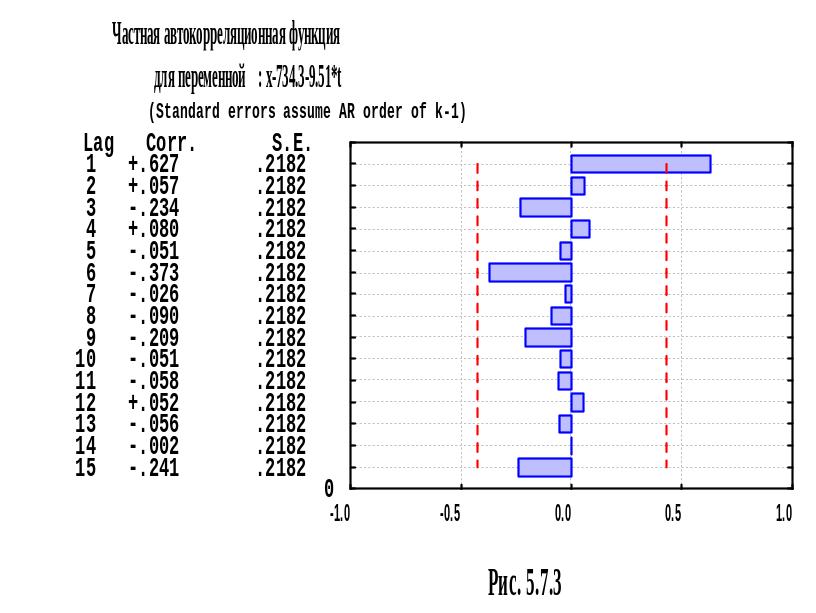 овим
параметр p-Autoregressive
в 1.
Затем нажмем на кнопку OK
(Begin
parameter
estimation),
после чего
начнется расчет параметра АР(1) модели
и будет выдан результат, автоматически
при этом произойдет смена закладки на
закладку Review&residuals
– анализ остатков. Но мы вернемся все
же на вкладку Advanced,
чтобы детальнее ознакомиться с
результатами расчета. Нажимая на кнопку
Summary:Parameter
estimates,
мы получим следующий результат:
p(1)=0.630204
при p<0.05,
следовательно,
модель значима.
овим
параметр p-Autoregressive
в 1.
Затем нажмем на кнопку OK
(Begin
parameter
estimation),
после чего
начнется расчет параметра АР(1) модели
и будет выдан результат, автоматически
при этом произойдет смена закладки на
закладку Review&residuals
– анализ остатков. Но мы вернемся все
же на вкладку Advanced,
чтобы детальнее ознакомиться с
результатами расчета. Нажимая на кнопку
Summary:Parameter
estimates,
мы получим следующий результат:
p(1)=0.630204
при p<0.05,
следовательно,
модель значима.
Теперь можно начать и непосредственно прогнозировать. Нажмем на кнопку Forecast cases. Получим следующие прогнозные значения для следующих за 21-м моментом времени.
22: -10.04233; 23: -6.3287; 24: -3.9884; 25: -2.5135; 26: –1.5840; 27: –0.9983; 28: –0.6291; 29: –0.3965; 30: –0.2499; 31: –0.1575. По умолчанию прогноз выполняется для 10 следующих моментов времени, но этот параметр может быть изменен. Прогноз выполнен только для переменной, которая получена после удаления тренда. Чтобы дать реальные значения прогноза, необходимо к этим прогнозным значениям добавить прогноз по тренду. Мы покажем это ниже в решении при помощи Excel. Там же мы приведем и окончательное аналитическое представление модели.
Насколько адекватна полученная модель реальности, мы судим по полученным остаткам модели. Поэтому зайдем на вкладку Autocorrelation и нажмем кнопку с таким же названием. Увидим, что АКФ ошибок, хотя и находится в доверительном интервале, но не склонна к уменьшению. Выберем вкладку Distribution of residuals и построим гистограмму ошибок. Видно, что распределение ошибок не очень-то подчиняется нормальному закону. Значит, к результатам прогноза надо отнестись с осторожностью.
Решение в Excel
Уравнение
тренда получаем при помощи режима
“Анализ данных”: регрессия. Устанавливается
зависимость между столбцами C
и B.
Результаты работы этого режима
записаны в ячейки С30:C31.
В столбце E
вычисляются
значения ряда ошибок как разница между
соответствующими значениями в столбцах
C
и D.
Так как для модели:![]() коэффициент
коэффициент
![]() есть по существу коэффициент регрессии
между значениями ряда, сдвинутыми
на 1 временной такт и прежним временным
рядом, в столбец F
записываем значения временного ряда
из столбца E
без первого элемента. Ищется регрессия
между членами ряда, записанного в столбце
F,
и членами ряда, записанного в столбце
E.
Понятно, что количество пар членов,
участвующих в нахождении регрессии,
уменьшилось на 1. Кроме того, необходимо
поставить галочку у параметра
“константа-ноль”. Результаты решения
показаны в ячейках F30:F31,
где в F31
имеем значение
параметра
,
совпадающее с ранее вычисленным значением
по программе STATISTICA.
есть по существу коэффициент регрессии
между значениями ряда, сдвинутыми
на 1 временной такт и прежним временным
рядом, в столбец F
записываем значения временного ряда
из столбца E
без первого элемента. Ищется регрессия
между членами ряда, записанного в столбце
F,
и членами ряда, записанного в столбце
E.
Понятно, что количество пар членов,
участвующих в нахождении регрессии,
уменьшилось на 1. Кроме того, необходимо
поставить галочку у параметра
“константа-ноль”. Результаты решения
показаны в ячейках F30:F31,
где в F31
имеем значение
параметра
,
совпадающее с ранее вычисленным значением
по программе STATISTICA.
Таблица 5.7.2
|
A |
B |
C |
D |
E |
F |
5 |
|
|
Показатель |
Тренд |
Ошибка |
|
6 |
|
|
|
|
|
|
7 |
1966 |
1 |
673 |
743.7792 |
-70.77922078 |
-59.287013 |
8 |
1967 |
2 |
694 |
753.287 |
-59.28701299 |
-51.794805 |
9 |
1968 |
3 |
711 |
762.7948 |
-51.79480519 |
13.697403 |
10 |
1969 |
4 |
786 |
772.3026 |
13.6974026 |
15.18961 |
11 |
1970 |
5 |
797 |
781.8104 |
15.18961039 |
-9.3181818 |
12 |
1971 |
6 |
782 |
791.3182 |
-9.318181818 |
9.174026 |
13 |
1972 |
7 |
810 |
800.826 |
9.174025974 |
21.666234 |
