7.Расчет цепей методом эквивалентного генератора.
Он применяется в тех случаях, когда необходимо определить ток только в одной ветви схемы. Токи в остальных ветвях не представляют интереса.
Последовательность расчета:
1. Отсоединить от схемы интересующую ветвь, клеммы подсоединения которой обозначить через а–б.
2. Рассчитать оставшуюся часть цепи и определить напряжение на клеммах а–б (Uаб).
3. В оставшейся части цепи заменить источники ЭДС перемычкой или резистором, сопротивление которого равно внутреннему сопротивлению источника ЭДС.
4. Определить сопротивление этой цепи относительно клемм а–б, которое обозначим R0.
5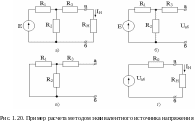
.
Оставшуюся часть цепи заменить
последовательно соединёнными источником
ЭДС с напряжением Uаб
и резистором с сопротивлением R0.
Эту цепь подсоединить к клеммам а–б.
6. К клеммам а–б подсоединить интересующую ветвь и определить ток, протекающий через нее.
Определим ток в ветви а–б схемы (рис. 1.20, а) методом эквивалентного источника напряжения.
Отключаем ветвь а–б (рис. 1.20, б) и находим напряжение на клеммах а–б:
.
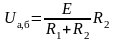Далее исключаем у оставшейся схемы источник E, заменяя его перемычкой, считая, что его внутреннее сопротивление равно нулю (рис. 1.20, в) и определяем сопротивление цепи относительно клемм а–б:
.
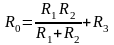Теперь составляем схему (рис. 1.20, г) и находим ток в ветви а–б:
.
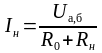Н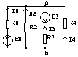
а
этом расчет закончен.
8.Расчет цепей методом двух узлов.
Рассмотрим схему, содержащую всего 2 узла.
Под методом двух узлов понимают метод расчета
электрических цепей, в котором за искомое принимают напряжение между двумя узлами схемы. In=(En – Uab)gn. Ток к узлу а и b
не подтекает. Поэтому если принять I=0, то
Uab=(ΣEk gk + ΣIk)/Σgk – напряжение. После этого можно найти ток в любой ветви: In=(En – Uab)gn.
9. Методы расчета нелинейных цепей.
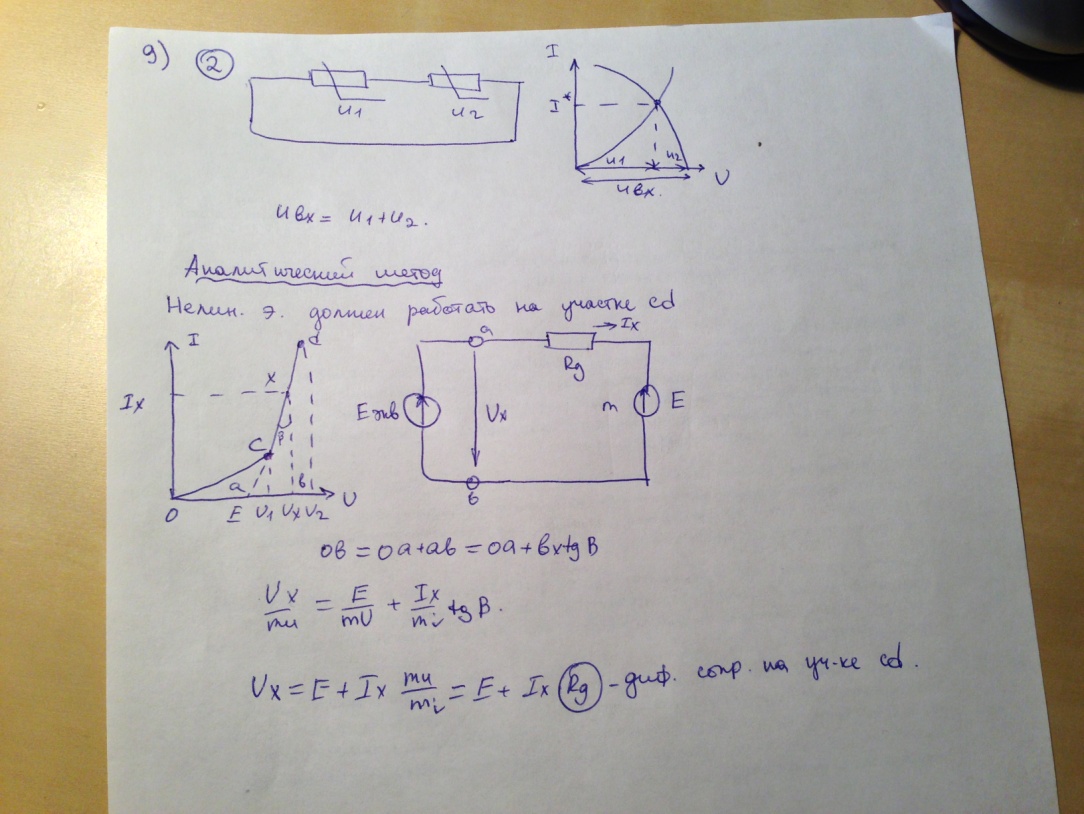
10.Параметры переменных токов и напряжений. Векторное представление активных величин.
1.Параметры переменного напряжения.
Переменное напряжение можно выразить через следующие параметры:
–
мгновенное
значение напряжения. Его измерение
осуществляется осциллографами
в i-й момент
времени;
–
пиковое
(амплитудное) значение напряжения –
максимальное значение напряжения за
время измерения или период колебания.
Если сигнал имеет разные пиковые значения
напряжения положительной и отрицательной
полярности, то они указываются отдельно
соответственно как 
,
;
–
среднее
значение напряжения (постоянная
составляющая). Для напряжения синусоидальной
формы, симметричного относительно оси
времени, среднее значение равно нулю;
–
среднее
выпрямленное значение напряжения;
–
действующее
значение напряжения.
Для сигналов одной полярности среднее значение и среднее выпрямленное значение напряжения равны.
Параметры напряжения синусоидальной формы показаны на рис. 3.1.
Рис. 3.1. Параметры напряжения синусоидальной формы
Связь
между величинами
, 
, 
определяется
коэффициентами: амплитуды 
;
формы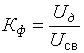 
;
усреднения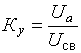 
.
Как видно, 
и 
.
2.Параметры переменного тока.
1. Мгновенное значение - величина тока соответствующая данному моменту времени
2. Амплитуда - максимальное мгновенное значение ( наибольшее значение, которого достигает переменный ток).
3
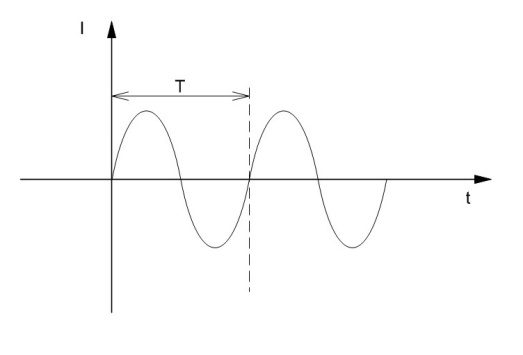. Период -
время в течение которого переменный
ток совершает полный цикл своих изменений,
возвращаясь к исходной величине.
Обозначается буквой Т
За один период совершается одно колебание переменного тока, т. е. период это время одного колебания. Одно колебание состоит из двух движений тока.
4. Частота - число колебаний переменного тока в секунду
5
. Фаза
- это
состояние переменного тока за определенный
период времени.
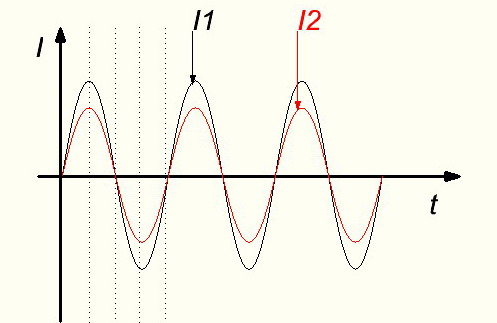
Переменные величины могут совпадать по фазе. Это значит что они одновременно достигают нулевых значений и одновременно достигают максимальных значений одинаковых направлений.
Здесь токи I1 и I2 совпадают по фазе
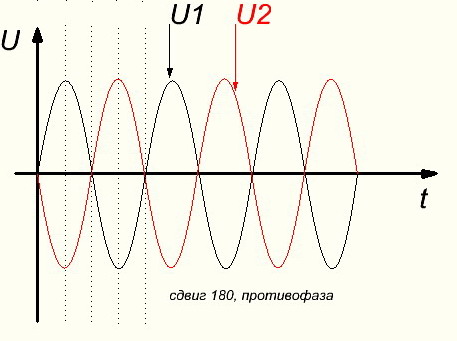
Здесь напряжения U1 и U2 находятся в противофазе.
Это значит что они одновременно достигают нулевых и максимальных значений противоположных направлений.
Если переменные величины не совпадают по фазе, то говорят что они сдвинуты по фазе.