3.1.2. Частный случай 2.

Пусть в начальный момент собака находится в центре круга О, а лиса – в точке Л₀ на расстоянии r₀ от центра, где r₀ меньше радиуса круга r. Условимся, что собака побежит так, чтобы всегда быть на радиусе ОЛ. Тогда лиса успеет спастись, если будет бежать по ломаной L.. Обозначим через С₁ точку, в которую прибежит собака, когда лиса окажется в точке Л₁. Так как С₁ находится на ОЛ₁, а Л₁Л₂ОЛ₁,то Л₁Л₂С₁Л₁ и собака не может поймать лису, пока та находится на Л₁Л₂. Это продолжается на каждом последующем звене ломаной: Л_nЛ_n+1С_nЛ_n и собака не может поймать лису на отрезке Л_nЛ_n+1(ни при каком n). Так как общая длина ломаной L бесконечна, то бесконечным будет и время, в течение которого лиса будет бежать по ней. Значит, ни за какое конечное время собака не сможет догнать лису.

Две суммы.

При изложении решения мы будем строить ломаные, состоящие из бесконечного множества все более коротких звеньев. Нужно будет, чтобы эти ломаные имели бесконечную длину, но целиком помещались внутри круга. Чтобы потом не прерывать изложения, проведем заранее некоторые вычисления. Выпишем две суммы:

, (1)

, (2)

Как они ведут себя при увеличении n? Возрастают – это ясно(потому что добавляются все новые положительные слагаемые). Но возрастают безгранично или становятся меньше некоторого числа? Оказывается, первая сумма с ростом n растет неограниченно, а вторая – при любом n меньше 1.

Доказательство:

1. Воспользуемся неравенствами:

,

,

и т.д.

Отсюда L₄1, L₈ , L₁₆2 и вообще для n = 2^k L_n . Если k равно двум миллионам, то L_n больше миллиона. Если k = 2*10⁹, то L_n больше миллиарда и т.д. Вообще, какое бы число N ни взять, найдется такое n, что L_n N(достаточно положить n=2^2М, где М – натуральное число, большее N, при mn неравенство L_mN выполняется и подавно). Итак, L_n с ростом номера n неограниченно возрастает.

2. Докажем, что K_n1 при любом n.

Вычислим сумму . Так как , то . Раскрыв скобки и перегруппировав слагаемые, получаем .

Так как , то . Итак, при любом n .

3.1.3.Частный случай 3.

Пусть, наконец, собака и лиса 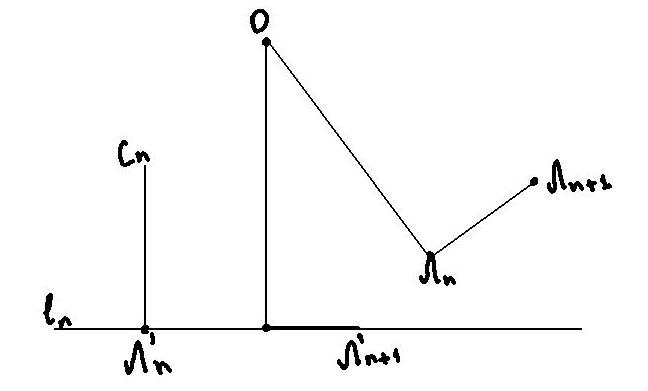находятся в начальный момент в двух произвольных(разумеется, различных) точках С₀ и Л₀ внутри круга радиуса r.

Мы покажем сейчас, что, как бы ни вела себя собака, лиса сможет убежать от нее. Рис. 14

Прежде всего, лиса «строит» описанную ранее ломаную L, но бежит вдоль другой ломаной L’, зависящей от того, что делает собака. Опишем построение ломаной L’.

Выбор точки Л₁. Проведем через точку Л₀ прямую l₀, перпендикулярную С₀Л₀. Пусть М₀ – основание перпендикуляра, опущенного из О на l₀. Точка Л₁ выбирается на продолжении Л₀М₀ так, чтобы выполнялось равенство М₀Л₁=Л₀Л₁(где Л₀Л₁ – первое звено ломаной L). Поэтому Л₀Л₁≥Л₀Л₁ и (ОЛ₁)²=ОМ₀²+М₀Л₁²≤ОЛ₀²+Л₀Л₁²=ОЛ₁².

Выбор точки Л_n+1. Из точки Л₀ лиса бежит в Л₁. Так как Л₀Л₁С₀Л₀, то, по кА лиса находится на Л₀Л₁, собака не может поймать ее. Обозначим через С₁ точку, в которую прибежит собака, когда лиса достигнет Л₁. Из Л₁ лиса должна бежать в Л₂. Выбор этой точки опишем сразу в общем виде: пусть собака и лиса находятся в разных точках С_n и Л_n, объясним, как тогда выбрать Л_n+1(рис. 14).

Проведем через Л_n прямую l_n перпендикулярную С_nЛ_n. Пусть M_n – основание перпендикуляра, опущенного из О на l_n. Точку Л_n+1 выберем на продолжении Л_nM_n на расстоянии Л_nЛ_n+1 от точки M_n(где Л_nЛ_n+1 – (n+1)-e звено ломаной L). Таким образом, Л_nЛ_n+1≥ M_nЛ_n+1= Л_nЛ_n+1. Теперь оценим ОЛ_n+1. Допустим, что точку Л_n нам удалось выбрать так, что ОЛ_n≤ ОЛ_n. Тогда поскольку ОM_n≤ ОЛ_n, выполняется неравенство (ОЛ_n+1)²= ОM_n²+ (M_nЛ_n+1)²≤ ОЛ_n²+ (Л_nЛ_n+1)² и тем самым ОЛ_n+1≤ОЛ_n+1.

Итак, каждое звено ломаной L’ не короче соответствующего звена L, а каждая вершина L’ расположена не дальше от центра О, чем соответствующая вершина L: Л_nЛ_n+1≥ Л_nЛ_n+1; ОЛ_n≤ОЛ_n. Иначе говоря, ломаная L’ имеет бесконечную длину, но целиком помещается в круге радиуса rс центром О. По построению С_nЛ_n Л_nЛ_n+1 при любом n. Значит, собака по-прежнему не сможет поймать лису.

Таким образом, как бы ни вела себя собака, лиса сможет от нее убежать.

5.Решение задач.

5.1.Постановка задачи 1

Пусть за лисой гонится из точки С₀ не собака, а охотник, стреляющий без промаха с расстояния r. Пренебрежем временем полета пули, то есть будем считать, что охотник догнал лису, если приблизился к ней на расстояние r. При каких С₀ лисе не убежать?

5.1.1.Решение задачи 1

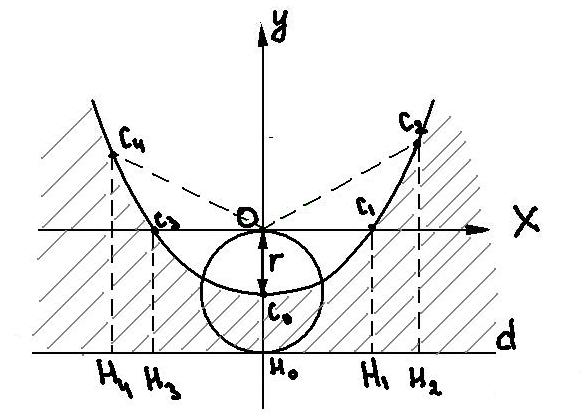
ОС₁=ОС₃=С₁Н₁=С₃Н₃

ОС₂=ОС₄=С₂Н₂=С₄Н₄

ОС₀=С₀Н₀

ОС₀ = r(радиус, с которого охотник может убить лису)

Зона безопасности заштрихована(если охотник находится в ней, то лиса сможет убежать).

Известно, что ОС₀ – максимальное расстояние, на которое охотник может приблизиться к лисе.

Если ОС₀ ≥ r, то охотник не сможет убить лису.

5.2.Постановка задачи 2

Может ли лиса на круглом отраженном участке убежать от двух собак, если известно, что у лисы и собак скорости равны и двигаться все могут как хотят?

5.2.1.Решение задачи 2

Известно, что лиса всегда сможет убежать от однойсобаки, если будет придерживаться ломанной L. Доказательство этого было основанно на том, чтто гипотинуза, по которой и побежит собака, всегда больше катета по которому бежит лиса.

Доказательство, что лиса сможет убежать от двух собак также должно основаваться на том, что траектории собак должны быть больше траектории лисы. Для этого нужно обратить внимание на то, что в тупоугольном треугольнике сторона расположенная против тупого угла является самой большой.

Алгоритм построения траектории движения лисы:

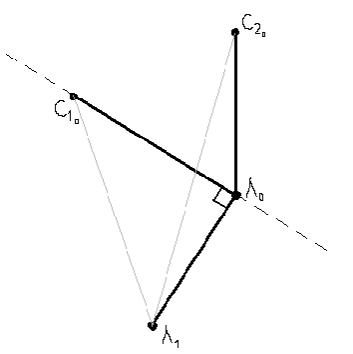
Необходимо провести прямую между лисой и одной из собак, которая будет разделять круглый участок на две (необезательно равные) части на одной из которых будет находится вторая собака, а надругой собак не будет. Затем нужно построить ломанную L относительно собаки через которую мы провели прямую в сторону противоположную второй собаки. Или если обе собаки расположены на одной прямой с лисой, то не важно в какую сторону строить ломанную L. На приложенном к задаче рисунке показан пример построения первого звина в ломанной L. угол С20 Л0 Л1 — тупой,что означает, что С20 больше Л0, значит эта собака безопасна для лисы, если та будет двигаться по ломанной L, до тех пор, пока собака С20 нахобится по другую сторону прямой. В случаи если собака С20 по мере движения пересечет прямую, то лисе нужно начать все заново, но теперь прямую провести не через С10, а через С20 и двигаться уже по новой ломанной L относительно собакиС20.

Если лиса будет придерживаться этого алгоритма, то сможет убежать от двух собак.