
- •1.2 Неподвижная система координат.
- •1.3. Движущейся система координат.
- •1.4. Движение по параболе.
- •2. Решение задачи
- •2.1. Решение
- •3. Задача про лису и собаку на ограниченном участке в форме круга.
- •3.1 Постановка задачи.
- •3.1.1. Частный случай 1.
- •3.1.2. Частный случай 2.
- •3.1.3.Частный случай 3.
- •6.Заключение
- •7. Литература
3. Задача про лису и собаку на ограниченном участке в форме круга.
3.1 Постановка задачи.
Теперь усложним предыдущую задачу.
Собака гонится за лисой на ограниченном участке в форме круга. Скорость собаки равна скорости лисы, причем лиса так же, как и собака, может бежать в любую сторону. Это задача похожа на задачу, придуманную Р.Радо, только у него вместо лисы и собаки фигурировали лев и человек. В его задаче спрашивалось: «Какой стратегии должен придерживаться лев, чтобы быть уверенным в своей трапезе?». В нашей задаче мы будем пытаться доказать обратное, а именно – какой стратегии нужно придерживаться лисе, чтобы собака не смогла ее догнать?
3.1.1. Частный случай 1.
 На
первый взгляд кажется, что лисе не
спастись, если собака выберет следующую
стратегию. Сначала она занимает место
в центре круга О, а затем бежит так, чтобы
все время находиться на радиусе ОЛ,
стараясь при этом максимально(насколько
позволяет скорость) приблизиться к
лисе. Лисе будто ничего не остается, как
бежать по окружности(не идти же ей самой
на сближение с собакой!). Что получится
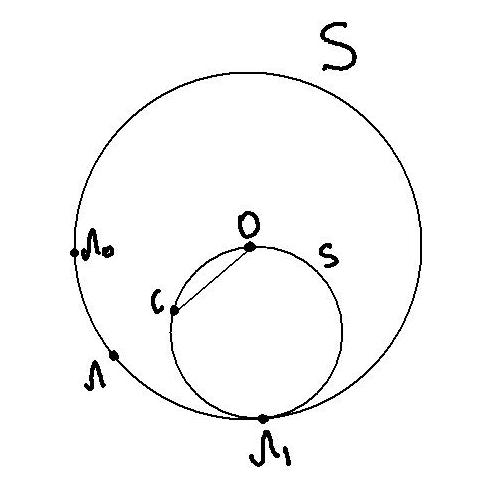
в этом случае, видно из рисунка 11. Когда
собака заняла центр О, лиса находилась
в точке Л0.
Обозначим через Л1
такую точку на окружности, что угол
Л0ОЛ1
= /2.
На отрезке ОЛ1
построим, как на диаметре, вспомогательную
окружность s.
Исходную(вдвое большую) – S,
и пусть Л – произвольная точка на дуге
Л0Л1,
а С – точка пересечения радиуса ОЛ и
окружности s.
Тогда
На
первый взгляд кажется, что лисе не
спастись, если собака выберет следующую
стратегию. Сначала она занимает место
в центре круга О, а затем бежит так, чтобы
все время находиться на радиусе ОЛ,
стараясь при этом максимально(насколько
позволяет скорость) приблизиться к
лисе. Лисе будто ничего не остается, как
бежать по окружности(не идти же ей самой
на сближение с собакой!). Что получится
в этом случае, видно из рисунка 11. Когда
собака заняла центр О, лиса находилась
в точке Л0.
Обозначим через Л1
такую точку на окружности, что угол
Л0ОЛ1
= /2.
На отрезке ОЛ1
построим, как на диаметре, вспомогательную
окружность s.
Исходную(вдвое большую) – S,
и пусть Л – произвольная точка на дуге
Л0Л1,
а С – точка пересечения радиуса ОЛ и
окружности s.
Тогда 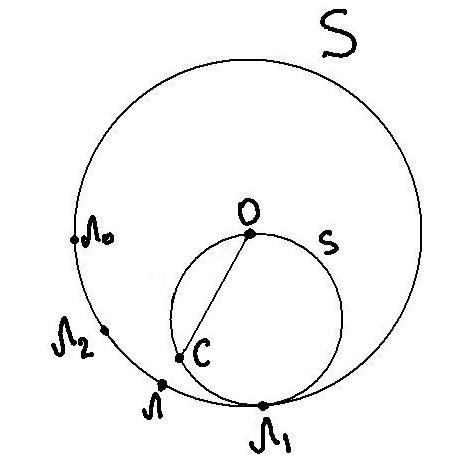 дуги
Л0Л
и ОС имеют одинаковую длину.
дуги
Л0Л
и ОС имеют одинаковую длину.
Таким образом, собака(руководствуясь выбранной стратегией) побежит из О в Л1 по окружности s; в точке Л1 она поймает лису. Рис. 11
Неожиданная смена направления на противоположное не поможет лисе: если лиса добежит до точки Л(рис. 12), а потом бросится назад в точку Л2, то собака(в соответствии со своей стратегией) побежит из С в Л2 по дуге, симметричной СЛ1 относительно радиуса ОЛ.
Итак, единственный шанс на спасение для лисы – сойти с окружности S. Навстречу собаке? Это представляется бессмысленным, и долгое время считалось, что лисе не избежать поимки.
 Сравнительно
недавно профессор А.С.Безикович опроверг
это заблуждение. Ниже мы приведем его
решение сначала в случае, когда собака
придерживается радиуса ОЛ, а потом – в
случае совершенно произвольного
Сравнительно
недавно профессор А.С.Безикович опроверг
это заблуждение. Ниже мы приведем его
решение сначала в случае, когда собака
придерживается радиуса ОЛ, а потом – в
случае совершенно произвольного
поведения собаки. Лисе в обоих случаях не нужно сразу убегать на окружность. Она должна отступать из некоторой внутренней точки круга очень постепенно, многократно меняя направление, по замысловатому Рис. 12
спиралеобразному пути.
Следствие. Пусть
О – центр круга радиуса r.
Л0
– точка на расстоянии r0
от центра, r0
r.
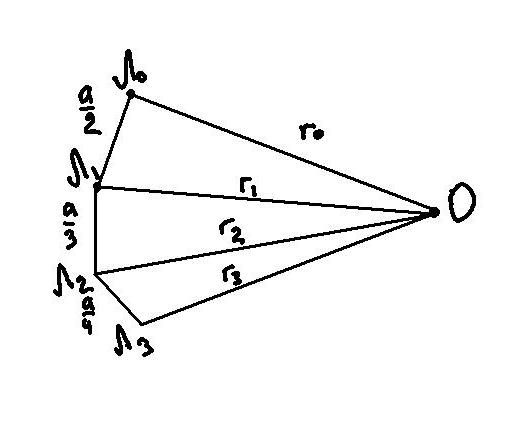
Положим, ![]() и построим ломаную L
так, что (рис. 13): Л0Л1
и построим ломаную L
так, что (рис. 13): Л0Л1![]() Л0Л1ОЛ0;
Л1Л2
=
Л0Л1ОЛ0;
Л1Л2
= ![]() ,
Л1Л2ОЛ1;
вообще Лn-1Лn
,
Л1Л2ОЛ1;
вообще Лn-1Лn
![]() ,
Лn-1Лn
ОЛn-1.
Тогда ломаная L
обладает следующими тремя свойствами:
Рис. 13
,
Лn-1Лn
ОЛn-1.
Тогда ломаная L
обладает следующими тремя свойствами:
Рис. 13
1)Она не выходит за пределы круга.
Действительно,
ОЛn2= ОЛn-12 + Лn-1Лn2, так что при любом n
ОЛn2![]()
2)Вместе с тем, поскольку
Л0Л1
+ Л1Л2
+ … + Лn-1Лn
![]() ,
то(при достаточно больших n)сумма
длин первых n
звеньев сколь угодно велика. Другими
словами, ломаная L
имеет бесконечную длину.
,
то(при достаточно больших n)сумма
длин первых n
звеньев сколь угодно велика. Другими
словами, ломаная L
имеет бесконечную длину.
3)Наконец, по построению каждое звено Лn-1Лn ломаной L перпендикулярно радиусу ОЛn-1.
