Содержание

Введение 2

1. Задача про лису и собаку, движущихся на неограниченном участке 3

1.1. Постановка задачи 3

1.2. Неподвижная система координат 3

1.3. Движущейся система координат 5

1.4.Движение по параболе 6

2. Решение задачи 7

2.1.Решение 7

3. Задача про лису и собаку на ограниченном участке в форме круга 9

3.1.Постановка задачи 9

3.1.1. Частный случай 1 9

3.1.2. Частный случай 2 11

3.1.3.Частный случай 3 12

5.Решение задач 15

5.1.Постановка задачи 1 15

5.1.1.Решение задачи 1 15

5.2.Постановка задачи 2 16

5.2.1.Решение задачи 2 16

6.Заключение 17

7.Литература 18

Введение.

В данной работе представлено исследование движения двух материальных точек, одна из которых условно догоняет другую, для наглядности обозначенных как лиса и собака.

Были рассмотрены два возможных случая: движение на неограниченном пространстве и на территории в форме круга, а также частные случаи для данной задачи(движение в неподвижной и подвижной системах координат, по параболе, по окружности и по ломаной).

Целю работы: было найти пути решения физических задач математическими методами.

Был изучен теоретический материал по теме движения материальных частиц и решению несколько практических задач на движение.

Данная работа может иметь практическое значение для изучения движения элементарных частиц и решения физических задач, в которых требуется определить взаимное расположение нескольких тел по определенному принципу, с учетом направления их движения. В результате проведенных исследований были установлены траектории движения тел в различных системах координат, доказанно ряд положений о взаимном расположении тел. Доказательная база была использована для решения поставленных задачь.

1. З адача про лису и собаку, движущихся на неограниченном участке. 1.1. Постановка задачи

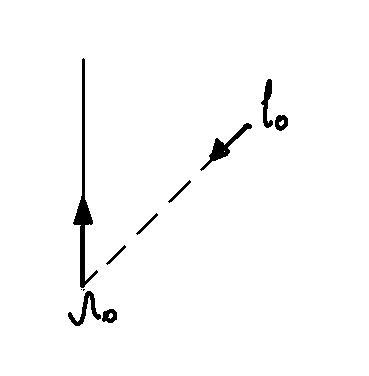
Лиса бежит по прямой с постоянной скоростью. Собака гонится за лисой с той же скоростью, причем бежит так, что видит лису все время перед собой. Лиса бежит из точки Л₀ в направлении, указанном стрелкой(рис. 1). Собака в начальный момент находится в точке С₀. При каких С₀ собака догонит лису? Рис.1

Иными словами задачу можно сформулировать следующим образом:

Дано: V₁ – постоянная скорость лисы

V₂ – та же скорость собаки

Л₀, С₀ – точки, в которых находятся лиса и собака

Найти: точки С₀, при которых собака догонит лису.

1.2 Неподвижная система координат.

Обозначим прямую, по которой бежит лиса Л, через L. В точке Л₀ поставим к ней перпендикуляр р(рис.2). Если собака находится в начальный момент на прямой L, все ясно:

Если С₀ расположена перед Л₀, то собака бежит навстречу лисе и ловит ее; Если С₀ – сзади Л₀, то собака никогда не догонит лису.

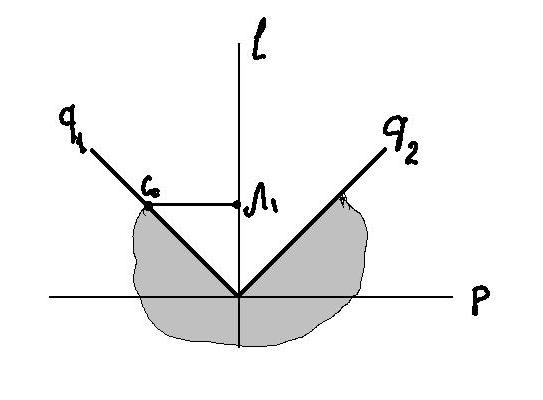
Если С₀ позади Л₀(ниже перпендикуляра р), то Рис. 2

лису не догнать.

Доказательство:

Разложим V₁на две составляющие – V₁ = V_L(вдоль L) + V_P(вдоль р).

Спроектируем точку С₀ на прямую L в точку П(С₀ПL).

Тогда V_L – скорость, с которой точка П движется вдоль прямой L вслед за Л.

Поскольку V_LV, то расстояние между П и Л не уменьшается с течением времени.

Так что собака в этом случае не догонит лису.

Точка С₀ – вне прямой L и впереди Л₀(выше перпендикуляра р).

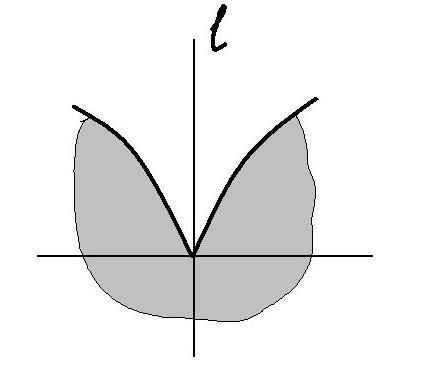
Проведем из точки два луча: Q₁ и Q₂ –под углом 45 к прямым L и р(рис. 3). Окрашенная зона безопасна для лисы: если С₀ находится в этой зоне, то собака, бегущая из точки С₀, не догонит лису.

Доказательство: Рис. 3

Возьмем точку С₀ даже не внутри, а на границе зоны – на луче Q₁. v – это вектор, а  - его длина.

Л – такая точка на прямой L, что С₀L  L.

Даже если бы собака бежала наперерез лисе по перпендикуляру С₀L, то и тогда она

Рис. 4

подбежала бы к прямой L лишь одновременно с лисой(Л₀Л₁=С₀Л₁).

На самом же деле, собака бежит к L по более длинному пути. Значит, когда лиса окажется в точке Л₁, собака еще не добежит до L. При этом она окажется позади лисы – за перпендикуляром С₀Л₁.

А в такой ситуации она не сможет догнать лису.

1.3. Движущейся система координат.

Теперь выберем прямоугольную систему координат (х,у) так, чтобы она равномерно двигалась вместе с лисой в направлении оси у.

Лиса:

Пусть в начальный момент лиса находилась в начале координат нашей движущейся системы(в точке О). Тогда она все время будет находиться в этой точке. Как будет двигаться собака относительно системы (х,у)?

Собака: Рис. 5а

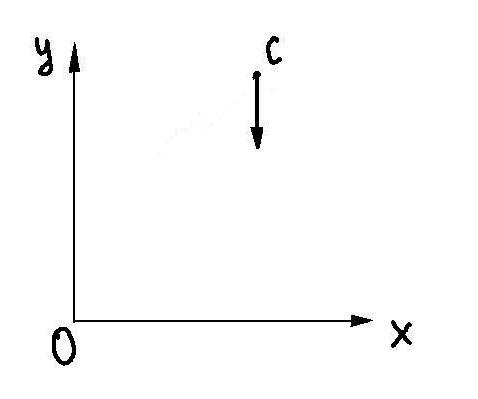Возьмем на плоскости (х;у) какую-нибудь точку С(рис. 5, а). Чтобы точка С находилась в покое с точки зрения неподвижного наблюдателя, нужно скомпенсировать движение системы (х,у), то есть нужно заставить точку С двигаться относительно системы (х,у) в направлении, противоположном направлению оси у, причем абсолютная величина скорости этого движения должна быть та же, что и у лисы(рис. 5, б).

Рис. 5б

П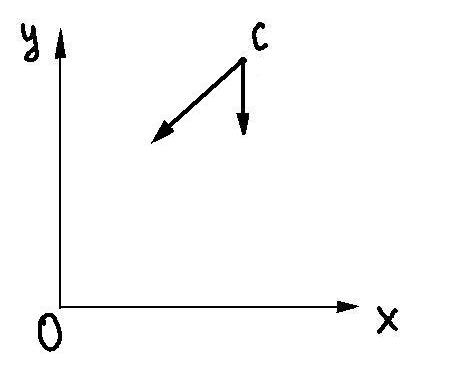 о условию задачи собака бежит прямо на лису. Значит, относительно системы (х,у) собака участвует в двух движениях: во-первых, равномерно движется со скоростью v направлении, противоположном оси у, во-вторых, приближается с той же скоростью к началу координат. Стрелки на рисунке 5, в – это

Рис. 5В

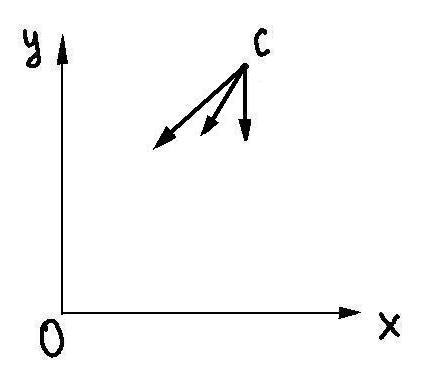векторы скоростей в каждом из указанных движений. Результирующая скорость движения собаки относительно системы координат (х,у) находится по правилу параллелограмма(рис. 5, г).

До сих пор мы рисовали точку С в одном и том же месте на плоскости (х,у). На рисунке 6 показано, как результирующая Рис. 5г

скорость зависит от расположения точки С.

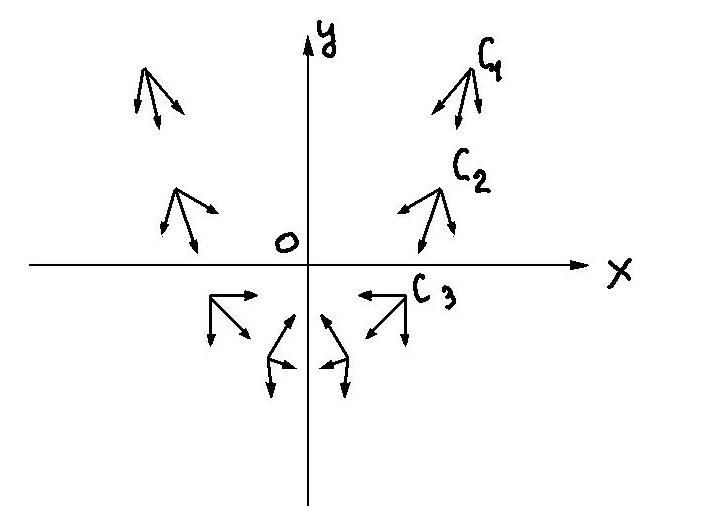Чем больше угол между векторами, которые складываются, тем короче вектор результирующей скорости. Если расположить точку С на отрицательной полуоси у, то векторы, которые складываются, будут иметь противоположные направления и результирующая скорость окажется равной нулю. Так, разумеется, и должно быть: если собака находится строго сзади Рис. 6

лисы, то она бежит за ней, не приближаясь и не отставая, то есть находится в состоянии покоя относительно системы (х,у).