10. Основной закон динамики вращательного движения.

Момент силы относительно точки. Момент импульса относительно точки. Вывод основного уравнения динамики вращательного движения.

Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку А приложения силы, на силу F (рис. 25):

М = [rF].

Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от г к F.

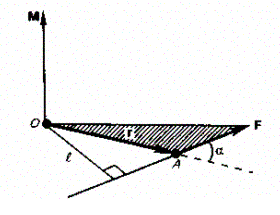
Рис. 25.

Модуль момента силы

где  — угол между г и F; rsin = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы.

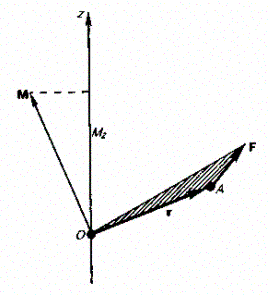
Рис. 26

Моментом силы относительно неподвижной оси z называется скалярная величина М_z, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 26). Значение момента М_г не зависит от выбора положения точки О на оси z.

Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

M_z = [rF]_z.

Найдем выражение для работы при вращении тела (рис. 27). Пусть сила F приложена в точке В, находящейся от оси z на расстоянии г,  — угол между направлением силы и радиусом-вектором г. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол d точка приложения В проходит путь ds=rd и работа равна произведению проекции силы на направление смещения на величину смещения:

Рис. 27

Учитывая (18.1), можем записать

где 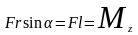— момент силы относительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота. Работа при вращении тела идет на увеличение его кинетической энергии: dA = dT, но 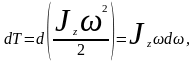поэтому 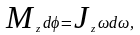или

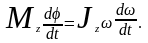
Учитывая, что 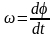, получаем

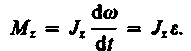(18.3)

Уравнение (18.3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Можно показать, что если ось z совпадает с главной осью инерции (см. § 20), проходящей через центр масс, то имеет место векторное равенство

(18.4)

где J — главный момент инерции тела (момент инерции относительно главной оси).

11. Закон сохранения момента импульса. Моментом импульса материальной точки относительно неподвижной точки. Момент импульса твердого тела. Закон сохранения момента импульса

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

где г — радиус-вектор, проведенный из точки О в точку A; p = mv — импульс материальной точки (рис. 28); L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от г к р.

Модуль вектора момента импульса

где  — угол между векторами г и р, / — плечо вектора р относительно точки О.

Рис. 28

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

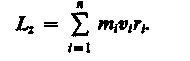
Используя формулу (17.1) v_i = r_i, получим

т. е.

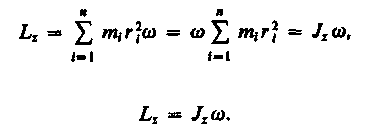(19.2)

Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость. Продифференцируем уравнение (19.2) по времени:

т. е.

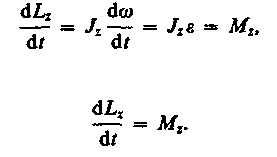
Это выражение — еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место векторное равенство

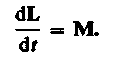(19.3)

В замкнутой системе момент внешних сил М = 0 и 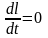, откуда

(19.4)

Выражение (19.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы от счета (относительно поворота замкнутой системы в пространстве на любой угол).

12. Механические колебания.

Колебательное движения (определение). Гармонические колебания и их характеристики (амплитуда, фаза, частота, период).Дифференциальное уравнение гармонических колебаний и его решение.

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т. Д

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воз действий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам:

1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;

2) различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний. Гармонические колебания величины s описываются уравнением типа

(140.1)

где А — максимальное значение колеблющейся величины, называемое амплитудой колебания, ₀ — круговая (циклическая) частота,  — начальная фаза колебания в момент времени t = 0, (₀t + ) — фаза колебания в момент времени t.

Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до - 1, то s может принимать значения от + А до - А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение 2, т. е.

откуда

(140.2)

Величина, обратная периоду колебаний,

(140.3)

т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (140.2) и (140.3), получим

Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, при которой за 1 с совершается один цикл процесса.

Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:

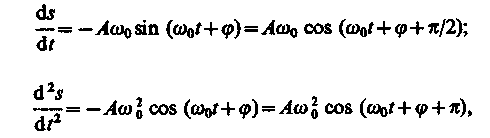(140.4) (140.5)

т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (140.4) и (140.5) соответственно равны А₀ и А²₀. Фаза величины (140.4) отличается от фазы величины (140.1) на /2, а фаза величины (140.5) отличается от фазы величины (140.1) на . 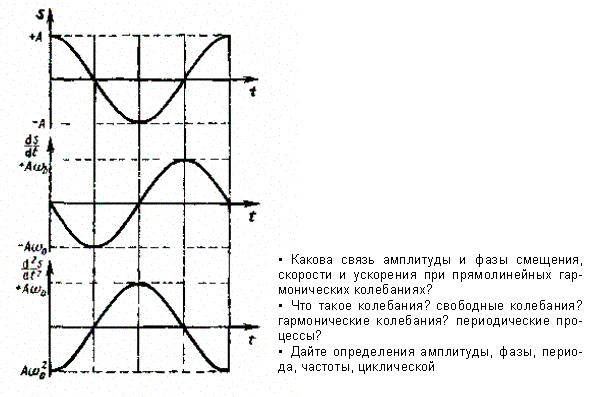Следовательно, в моменты времени, когда s = 0, ds/dt приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то d²s/dt² приобретает наибольшее положительное значение (рис. 198). Рис. 198

Из выражения (140.5) следует дифференциальное уравнение гармонических колебаний

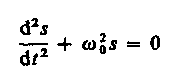(140.6)

(где s = A cos (₀t + )). Решением этого уравнения является выражение (140.1).

(140.1)