Проверка значимости коэффициентов простой линейной регрессии и адекватности регрессионной модели.

1. F-тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы H0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт  и критического (табличного) Fтабл значений F-критерия Фишера. Fфакт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где   n – число единиц совокупности;

        m – число параметров при переменных x.

Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a  –  вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.

Если  Fтабл< Fфакт, то H0  – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если  Fтабл> Fфакт, то H0 – гипотеза не отклоняется и признается статистическая незначимость, надежность уравнения регрессии.

2.  t-критерий Стьюдента используется для оценки статистической значимости коэффициентов регрессии и коэффициента  корреляции.

В качестве основной гипотезы вы­двигают гипотезу H0 о незначимом отличии от нуля параметра регрессии или коэффициента корреляции. Альтернативной гипотезой, при этом является гипотеза обратная, т.е. о неравенстве нулю параметра или коэффициента корреляции.

Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактиче­ским) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (ко­торые обычно приводятся в конце учебников и практикумов по статистике или эконометрике).

Табличное значение оп­ределяется в зависимости от уровня значимости (a) и числа степеней свободы, которое в случае линейной парной рег­рессии равно (n-2) , n - число наблюдений.

Если фактическое значение t-критерия больше таб­личного (по модулю), то считают, что с вероятностью (1-a) параметр регрессии (ко­эффициент корреляции) значимо отличается от нуля.

Если фактическое значение t-критерия меньше таб­личного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр регрессии (коэффициент корреля­ции) незначимо отличается от нуля при уровне значимости a.

Фактические значения t-критерия определяются по формулам:

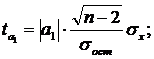
где  

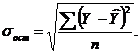
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции используют критерий:

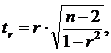
где r - оценка коэффициента корреляции, полученная по наблюдаемым данным. tтабл  остается прежним.

 

3.  Адекватность регрессионной модели оценим с помощью средней ошибки аппроксимации – среднее отклонение расчетных значений от фактических:

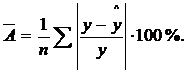
Допустимый предел значений    –  не более 8-10%.

3. Семь простейших инструментов качества. Диаграмма Парето. Этапы построения. Принцип Парето.

Диаграмма Парето — инструмент, позволяющий распределить усилия для разрешения возникающих проблем и выявить основные причины, с которых нужно начинать действовать.

Построение диаграммы Парето состоит из следующих этапов.

Этап 1. Сначала следует решить:

1. какие проблемы необходимо исследовать (например, дефектные изделия, потери в деньгах, несчастные случаи);

2. какие данные нужно собрать и как их классифицировать (например, по видам дефектов, по месту их появления, по процессам, по станкам, по рабочим, по технологическим причинам, по оборудованию, по методам измерения и применяемым измерительным средствам; нечасто встречающиеся признаки объединяют под общим заголовком «прочие»);

3. определить метод и период сбора данных.

Этап 2. Разработка контрольного листка для регистрации данных с перечнем видов собираемой информации.

Этап 3. Заполнение листка регистрации данных и подсчет итогов.

Этап 4. Разработка таблицы для проверок данных с графами для итогов по каждому проверяемому признаку в отдельности, накопленной суммы числа дефектов, процентов к общему итогу и накопленных процентов (табл. 1).

Этап 5. Расположение данных, полученных по каждому проверяемому признаку, в порядке значимости и заполнение таблицы (см. табл. 1).

Таблица 1. Результаты регистрации данных по типам дефектов для построения диаграммы Парето.

Типы дефектов

Число дефектов

Накопленная сумма числа дефектов

Процент числа дефектов по каждому признаку к общей сумме

Накопленный процент

Группу «прочие» следует размещать в последней строке независимо от ее числовых значений, поскольку ее составляет совокупность признаков, числовой результат по каждому из которых меньше, чем самое маленькое значение, полученное для признака, выделенного в отдельную строку.

Этап 6. Нанесение горизонтальной и вертикальной осей.

Вертикальная ось содержит проценты, а горизонтальная — интервалы в соответствии с числом контролируемых признаков.

Горизонтальную ось разбивают на интервалы в соответствии с количеством контролируемых признаков.

Этап 7. Построение столбиковой диаграммы (рис. 1).

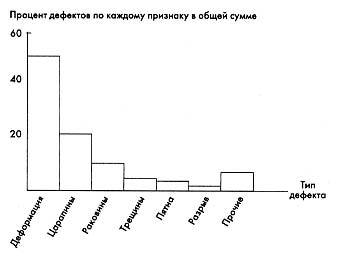
Рисунок 1. Диаграмма Парето

Этап 8. Проведение на диаграмме кумулятивной кривой (кривой Парето) (рис. 2).

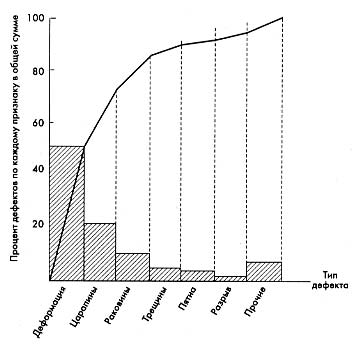
Рисунок 2. Кумулятивная кривая на диаграмме Парето

Этап 9. Нанесение на диаграмму всех обозначений и надписей, касающихся диаграммы и данных