Билет №3

1. Теория статистики как научная база при изучении курса «смКиУк»

Функционирование предприятия во многом зависит от уровня системы менеджмента. Основной целью системы менеджмента качества (СМК) является достижение максимального соответствия результатов работы предприятия – производства товаров и/или услуг – явным требованиям и подразумеваемым потребностям потребителя, организации и общества.

А главная задача, которая ставится перед СМК– это постоянное улучшение качества производимых товаров и услуг за счет регулярного контроля аналитических данных и необходимой корректировки деятельности, полное устранение дефектов и непроизводственных затрат, а также четкое выполнение поставленных задач в срок.

При осуществлении деятельности СМК на предприятии используется целый набор методических средств, которые помогают быстро и эффективно решать поставленные задачи. Среди них важное место занимают методы, относящиеся к области статистики

• средства сбора и предоставления данных;

• методы обработки статистических данных;

• методы, которые относятся непосредственно к теории менеджмента: системный анализ производства, экономические расчеты, управление с помощью планирования СМК.

Применение базовых статистических характеристик изменчивости процессов (среднее, стандартное отклонение, коэффициент вариативности, С_р и т.д.) дают возможность численно измерять процесс и отслеживать тенденции.

2.Линейная регрессия. Гипотезы о значении коэффициентов линейной регрессии.

ЛИНЕЙНАЯ РЕГРЕССИЯ

одной случайной переменной Y=(Y⁽¹⁾, ..., Y^(m))' по другой Х=(Х ⁽¹⁾, ..., Х ^(p))' - линейная по xm-мерная векторная форма, описывающая зависимость условного математич. ожидания (при условии Х=x).случайного вектора Y от значений x = (х ⁽¹⁾ ..., х ^(p))'. Соответствующие уравнения

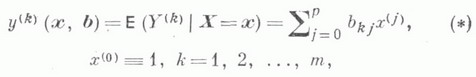
наз. уравнениями линейной регрессии Y по X, а параметры b_kj - коэффициентами регрессии.

В приложениях допускается интерпретация переменной X как наблюдаемого параметра (не обязательно случайного), от к-рого зависит математич. ожидание исследуемого результирующего показателя Y(X). Кроме того, часто под Л. р. Y^(k) по X понимают "наилучшую" (в определенном смысле) линейную аппроксимацию Y^(k) посредством величин X или результат наилучшего

(в определенном смысле) выравнивания имеющейся системы экспериментальных точек ("наблюдений") с помощью гиперплоскости в пространстве в ситуациях, когда интерпретация совокупности этих точек как выборки из соответствующей генеральной совокупности может и не быть правомочной. При таком определении приходится различать разные варианты Л. р. в зависимости от выбора способа вычисления ошибки линейной аппроксимации Y^(k) посредством величин X (или в зависимости от конкретного выбора критерия качества выравнивания). Наиболее распространенными критериями качества аппроксимации Y^(k) с помощью линейных комбинаций X (линейного выравнивания точек ) являются:

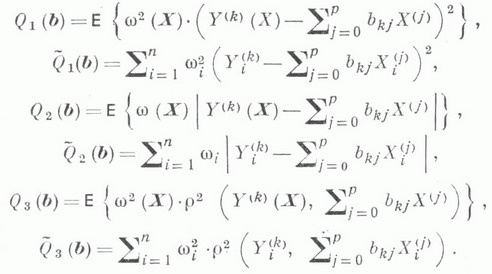
В этих соотношениях выбор "весов" w(X) или w_i зависит от природы конкретной исследуемой схемы. Так, напр., если Y^(k)(X) интерпретируются Как случайные величины, дисперсия к-рых (или их оценки) известны, то В последних двух критериях "невязки" аппроксимации или выравнивания измеряются расстояниями от Y^(k)(X )или до искомой гиперплоскости регрессии. Если коэффициенты b_ki определяются из условия минимизации величин то Л. р. наз. средней квадратической; при использовании критериев Л. р. наз. средней модульной (или средней абсолютной); при использовании критериев - ортогональной. В не-к-рых случаях Л. р. в классич. смысле (*) совпадает с Л. р., определенной с использованием функционалов типа Q_i. Так, напр., если вектор подчиняется многомерному нормальному закону, то регрессия Y^(k) по X в смысле (*) совпадает со средней квадратичсской Л. р. (при w(X)=1).