Билет №25

1. Спк кп поставщика методом толерантных границ. Три возможных случая задания предельных значений показателя качества при контроле.

7.10.2. Метод толерантных границ применяют только для случая одного показателя качества. Возможны три случая задания предельных значений показателя качества.

Случай А. Задано наименьшее предельное значение показателя качества изделия: у > а.

По результатам СПК рассчитывают нижнюю толерантную границу 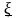уровня доверия: g₀ = 1 - b₀.

Решение о соответствии партии продукции требованию к качеству принимают, если нижняя толерантная граница не меньше наименьшего предельного значения показателя качества: .

Решение о несоответствии принимают, если .

Случай Б. Задано наибольшее предельное значение показателя качества изделия: у £ b.

По результатам СПК рассчитывают верхнюю толерантную границу уровня доверия: g₀ = 1 - b₀.

Решение о соответствии принимают, если .

Решение о несоответствии принимают, если .

Случай В. Заданы наименьшее и наибольшее предельные значения показателя качества изделия: а £ у £ b.

По результатам СПК рассчитывают нижнюю и верхнюю толерантные границы, соответствующие уровням доверия , , причем .

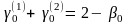Решение о соответствии принимают, если одновременно выполнены условия: ³ а или £ b.

Решение о несоответствии принимают, если выполнено хотя бы одно из условий: < а или > b.

2. Коэффициент конкордации.

В нечисловой статистике часто возникает необходимость установления степени взаимосвязи (корреляции), или сходства двух, или более объектов. При этом традиционные подходы, основанные на формулах Пирсона, Спирмена и ранговой конкордации Кендалла, часто не дают нужного результата при недостаточной согласованности объектов по одному из измерений и малом объеме исходной выборки (см., например, [1] и [2]). Кроме того, данные формулы требуют предварительной обработки при равенстве рангов объектов.

Для решения данной проблемы предлагается использовать модифицированный коэффициент конкордации:

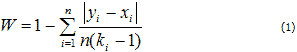
где

n - объем выборки,

ki - количество признаков по i-му элементу выборки. В случае, когда   вид (1) упрощается:

Формула (2) является аналогом коэффициента конкордации Кендалла:

но не имеет ограничений, налагаемых на формулу (3). Например, для определения корреляции между результатами, полученными студентами при сдаче экзамена в традиционной форме и в форме компьютерного теста (см. таблицу 1), формула Кендалла требует рангового преобразования пятибалльной (фактически, четырехбалльной, так как оценка 1 не ставится) шкалы оценок с последующим усреднением показателей для равных рангов (см. таблицу 2).

Исходные данные. (Таблица 1).

Студенты	1	2	3	4	5	6	7	8	9	10
Тест	2	3	3	3	4	4	4	4	5	5
Экзамен	4	3	3	3	3	4	4	4	5	5

Входные данные для формул Спирмена и Кендалла. (Таблица 1).

Студенты	1	2	3	4	5	6	7	8	9	10
Тест	1	3	3	3	6,5	6,5	6,5	6,5	9,5	9,5
Экзамен	6,5	3,5	3,5	3,5	3,5	6,5	6,5	6,5	9,5	9,5

Подобные преобразования требуют дополнительных временных затрат, как за счет собственно затрат на преобразования, так и за счет перевода исходных данных в вещественное представление.

Модифицированный коэффициент конкордации (1) может работать непосредственно по исходным данным. При этом необходимо либо уменьшить все значения в таблице 1 на единицу, так как мы имеем дело с четырехбалльной шкалой, либо привести (1) к виду:

где

n - объем выборки,

k - максимально возможное значение признака (в нашем случае k=5),

m - минимально возможное значение признака (в нашем случае m=2).

При этом выполняется интуитивно понятное требование, по которому значение коэффициента конкордации должно быть не меньше, чем 0.8, так как в исходной таблице различаются значения только в двух столбцах из десяти - в первом и пятом (модифицированный коэффициент конкордации, рассчитанный по формуле (4) будет равен 0.9). В то же время, коэффициент конкордации Кендалла, рассчитанный по таблице 2 и формуле (3), будет приблизительно равен 0.64, что, с точки зрения статистики, является достаточно плохим результатом, практически говорящим об отсутствии связи между данными, полученными с помощью тестирования и экзамена.