3. Семь простейших инструментов качества. Гистограмма. Этапы построения. Типичные формы гистограмм.

Гистограммы – один из вариантов столбчатой диаграммы, отображающий зависимость частоты попадания параметров качества изделия или процесса в определенный интервал значений от этих значений.

Из таблицы определяем, что минимальный размер скобы xmin = 9,793 мм, а максимальный xmax = 10,195 мм.

Вычисляем диапазон значений:

R = xmax - xmin = 10,195 - 9,793 = 0,402 мм.

Рассчитываем количество интервалов гистограммы по формуле:

Округляем полученное значение до целого числа в соответствии с общепринятым правилом и получаем n = 14 .

Определяем ширину интервалов:

H = R / n = 0,402 / 14 = 0,0287 мм.

Округляем в большую сторону и получаем H = 0,03 мм (можно округлить и до значения 0,029 мм, но 0,03 мм намного удобнее для дальнейшего использования).

PыSы В данном случае получение 0,03 мм из 0,0287 мм происходит в соответствии с общепринятым правилом округления. Но, если бы мы получили, к примеру, 0,0212 мм, то округляя в большую сторону, получили бы тоже 0,03 мм.

Нижнюю границу берем меньше минимального значения – 9,79 мм.

Определяем границы интервалов:

9,79 + 0,03 = 9,82 получаем интервал 9,79 – 9,82 мм,

9,82 + 0,03 = 9,85 получаем интервал 9,82 – 9,85 мм,

9,85 + 0,03 = 9,88 получаем интервал 9,85 – 9,88 мм,

и т.д. Таким образом, получаем границы для всех 14 интервалов.

Последний полученный интервал 10,18 – 10,21 мм.

В нашем случае границы допуска совпали с границами интервалов, поэтому дальнейшей подгонки границ интервалов к границам допуска не требуется.

Подсчитываем частоту попадания измеренных размеров скобы (указанных в вышеприведенной таблице) для каждого интервала и заполняем таблицу: Вычисляем среднее значение для ширины скобы:

Чертим горизонтальную и вертикальную оси.

Делим горизонтальную ось на интервалы, оставляя перед первым и после последнего интервала свободное место.

Т.к. максимальная частота попадания – 22, то выбираем диапазон – 25 и масштаб – 5. Наносим на вертикальную ось шкалу с выбранными диапазоном и масштабом.

Строим гистограмму на основе данных таблицы п.6.

Наносим на график линии среднего значения ширины скобы и границ поля допуска.

В результате получаем:

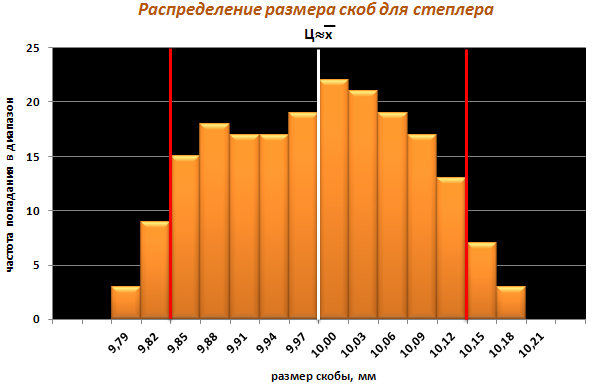
Обычная (симметричная, колоколообразная) форма. Среднее значение гистограммы соответствует середине размаха данных. Максимальная частота также приходится на середину и постепенно уменьшается к обоим концам. Форма симметричная. 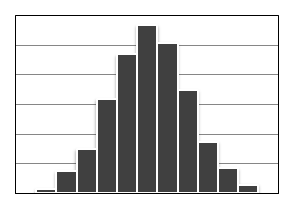Такая форма гистограммы встречается наиболее часто. Она свидетельствует о стабильности процесса.

Отрицательно скошенное распределение (положительно скошенное распределение). Среднее значение гистограммы располагается правее (левее) середины размаха данных. Частоты резко уменьшаются при движении от центра гистограммы вправо (влево) и медленно влево (вправо). Форма ассиметричная.

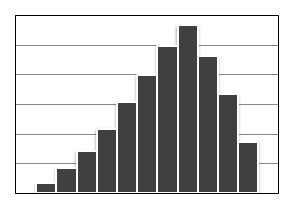
Такая форма образуется либо, если верхняя (нижняя) граница регулируется теоретически или по значению допуска либо, если правое (левое) значение невозможно достигнуть.

Распределение с обрывом справа (распределение с обрывом слева). Среднее значение гистограммы располагается далеко правее (левее) середины размаха данных. Частоты очень резко уменьшаются при движении от центра гистограммы вправо (влево) и медленно влево (вправо). Форма ассиметричная.

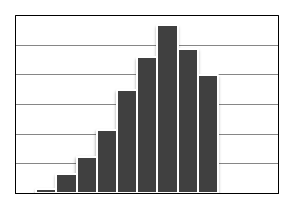
акая форма часто встречается в ситуации 100 %-го контроля изделий по причине плохой воспроизводимости процесса.

Гребенка (мультимодальный тип). Интервалы через один или два обладают более низкими (высокими) частотами.

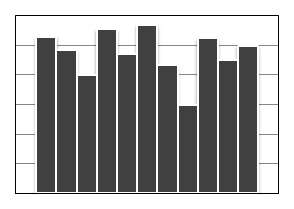
Такая форма образуется либо, если количество единичных наблюдений, входящих в интервал, колеблется от интервала к интервалу либо, если применяется определенное правило округления данных.

Гистограмма, не имеющая высокой центральной части (плато). Частоты в середине гистограммы примерно одинаковые (для плато все частоты примерно равны).

Такая форма встречается, если объединяется несколько распределений со средними значениями близко расположенными друг к другу. Для дальнейшего анализа рекомендуется применить метод стратификации.

Двухпиковый тип (бимодальный тип). В окрестностях середины гистограммы частота низкая, но с каждой стороны есть по пику частот. 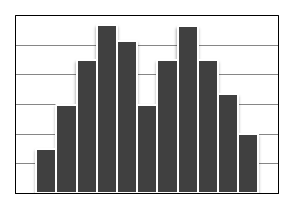Данная форма встречается, если объединяется два распределения со средними значениями, далеко отстоящими друг от друга. Для дальнейшего анализа рекомендуется применить метод стратификации.