Вопрос 2

На втором этапе систем управления качеством (1920–1950‑е гг.)

развитие получили статистические методы контроля качества –

SQC (А. Шухарт, Г.Ф. Додж и др.). Появились контрольные кар‑

ты, обосновывались выборочные методы контроля качества про‑

дукции и регулирования техпроцессов.

Для выявления точности процесса, полей рассеяния показателей качества используются статистические методы управления качеством( диаграммы рассеяния, карты Шухарта)

Диаграмма рассеяния применяется, когда требуется представить, что происходит с одной из переменных величин, если другая переменная изменяется, и проверить предположение о взаимосвязи двух переменных величин. Диаграмма рассеяния используется для изучения возможной связи между двумя переменными величинами. Глядя на диаграмму рассеяния нельзя утверждать, что одна переменная служит причиной для другой, однако диаграмма проясняет, существует ли связь между ними и какова сила этой связи. Диаграмма рассеяния строится в таком порядке: по горизонтальной оси откладываются измерения величин одной переменной, а по вертикалькой оси - другой переменной.

Одним из основных инструментов в обширном арсенале статистических методов контроля качества являются контрольные карты.

Контрольная карта (рис. 4.8) состоит из центральной линии, двух контрольных пределов (над и под центральной линией) и значений характеристики (показателя качества), нанесенных на карту для представления состояния процесса. Сигналом о возможной разладке технологического процесса могут служить:

• выход точки за контрольные пределы (точка 6); (процесс вышел из-под контроля)

• расположение группы последовательных точек около одной контрольной границы, но не выход за нее (11, 12, 13, 14), что свидетельствует о нарушении уровня настройки оборудования

• сильное рассеяние точек (15, 16, 17, 18, 19, 20) на контрольной карте относительно средней линии, что свидетельствует о снижении точности технологического процесса

При наличии сигнала о нарушении производственного процесса должна быть выявлена и устранена причина нарушения. Таким образом, контрольные карты используются для выявления определенной причины, но не случайной. Под определенной причиной следует понимать существование факторов, которые допускают изучение. Разумеется, что таких факторов следует избегать. Вариация же, обусловленная случайными причинами необходима, она неизбежно встречается в любом процессе, даже если технологическая операция проводится с использованием стандартных методов и сырья. Исключение случайных причин вариации невозможно технически или экономически нецелесообразно.

целями применения контрольных карт могут быть:

1. выявление неуправляемого процесса

2. контроль за управляемым процессом

3. оценивание возможностей процесса

Обычно подлежит изучению следующая переменная величина (параметр процесса) или характеристика:

• известная важная или важнейшая

• предположительная ненадежная

• по которой нужно получить информацию о возможностях процесса

• эксплуатационная, имеющая значение при маркетинге

При этом не следует контролировать все величины одновременно.

Обычные и особые причины вариаций технологических процессов

В производстве всегда существует вариабельность (изменчивость) качества продукта и параметров процесса, в котором этот продукт создается. Отклонения от заданных значений называются вариациями.

Своим происхождением вариации обязаны двум принципиально разным источникам, которые принято называть обычными и особыми причинами вариаций.

Обычными причинами вариаций называют причины, являющиеся неотъемлемой частью данного процесса и внутренне ему присущие. Они связаны с неабсолютной точностью автоматического, полуавтоматического или ручного поддержания параметров и условий осуществления процесса. Другими словами, это — результат совместного воздействия большого числа случайных факторов, каждый из которых вносит свой вклад в результирующую вариацию. Обычные причины вариаций ведут себя как стабильная система случайных причин. Если действуют только обычные причины, выход процесса предсказуем. Вариация, вызванная обычными причинами, уменьшается при подборе более совершенного оборудования, более точных и надежных приборов контроля и т.д. Численно обычные причины вариации оцениваются по коэффициентам воспроизводимости (Cp, Cpk), визуально – по картам Шухарта, но оценка корректна только при условии, что отсутствуют специальные причины.

Особые причины вариаций - это те причины, которые возникают из-за внешних по отношению к процессу воздействий на него и не являются его неотъемлемой частью. Они связаны с приложением к процессу незапланированных воздействий, не предусмотренных его нормальным ходом, а также неправильной работой приборов и датчиков. Если они возникают, то вызывают изменение распределения общего процесса. Если они не идентифицированы и не устранены, то они будут влиять на выход процесса непредсказуемым образом, а выход процесса будет нестабилен во времени. Особые причины вариаций уменьшаются при постоянном их отслеживании, обнаружении и устранении. Обнаруживаются и оцениваются визуально или в автоматическом режиме только по контрольным картам Шухарта.

Борьба с вариабельностью процесса требует различного подхода для каждого из этих случаев. Обычные причины вариаций требуют вмешательства в систему (внедрение более совершенного оборудования и приборов контроля), а особые причины вариаций требуют локального вмешательства в процесс.

Билет 13 вопрос 3.

Среди простых статистических методов, названных так ввиду их сравнительной несложности, убедительности и доступности, наибольшее распространение получили семь методов, выделенных в начале 50-х годов японскими специалистами под руководством К. Исикавы. В своей совокупности эти методы образуют эффективную систему методов контроля и анализа качества. С их помощью, по свидетельству самого К. Исикавы, может решаться от 50 до 95% всех проблем, находящихся в поле зрения производственников.

Расслоение данных (стратификация) представляет собой группировку данных на страты (группы). На практике стратификация используется для расслаивания статистических данных по различным признакам и анализа выявленной при этом разницы в диаграммах Парето, схемах Исикавы, гистограммах, диаграммах рассеивания и т.д.

Диаграмма Парето - разновидность столбиковой диаграммы применяемой для наглядного отображения рассматриваемых факторов в порядке уменьшения их значимости. 

Причинно-следственная диаграмма. Она позволяет выявить и систематизировать различные факторы и условия , оказывающие влияние на рассматриваемую проблему .

Гистограмма представляет собой один из видов столбиковой диаграммы, дающей наглядное представление того, с какой частотой повторяется то или иное значение или группа значений.

Диаграмма разброса. Диаграмма разброса используется для выявления зависимости между показателями качества (результат) и основными факторами производства (причина) при анализе причинно-следственной диаграммы или для выявления корреляционной зависимости между факторами.

Контрольные карты. 

Контрольный листок служит для сбора и упорядочения первичных данных. 

Гистограмма строится на основе результатов измерений в виде ступенчатой фигуры. Весь диапазон полученных данных разбивается на несколько интервалов.

Для оценки качества процесса по гистограммам отмечают нижнюю и верхнюю границы поля допуска и через них проводят две прямые устанавливающие возможные значения параметра качества. Если все значения будут находится в поле допуска, то процесс стабильный и устойчивый. Если появляется отклонения, то изучается причина и она устраняется.

Типовые формы гистограмм

  

Полезную информацию о характере распределения случайной величины можно получить, взглянув на форму гистограммы.

 Обычная форма (симметричная, или колоколообразная). Среднее значение гистограммы приходится на середину размаха данных. Наивысшая частота оказывается в середине и постепенно снижается к обоим концам. Форма симметрична.

 Гребенка Интервалы через один имеют более низкие (высокие) частоты.

 Такая форма встречается, когда число единичных наблюдений, попадающих в интервал, колеблется от интервала к интервалу или когда действует определенное правило округления данных.

 

Положительно скошенное распределение (отрицательно скошенное распределение). Среднее значение гистограммы локализуется слева (справа) от центра размаха. Частоты довольно резко спадают при движении влево (вправо) и, наоборот, медленно — при движении вправо (влево). Форма асимметрична.

 Такая форма встречается, когда левое (правое) значение поля допуска недостижимо.

 

Распределение с обрывом справа (распределение с обрывом слева). Среднее арифметическое гистограммы локализуется далеко слева (справа) от центра размаха. Частоты резко спадают при движении влево (вправо) и, наоборот, медленно вправо (влево). Форма асимметрична.

 Это одна из тех форм, которые часто встречаются при 100 %-ной разбраковке изделий из-за плохой управляемости процесса, а также когда проявляется резко выраженная положительная (отрицательная) асимметрия.

 

Равномерное или прямоугольное распределение (плато). Частоты в разных интервалах образуют плато, поскольку все интервалы имеют более или менее одинаковые ожидаемые частоты.

 Такая форма встречается в смеси нескольких распределений, имеющих различные средние значения.

 

Двухпиковая (бимодальная) форма. В окрестностях центра диапазона данных частота низкая, т. е. по пику с каждой стороны.

 Такая форма встречается, когда смешиваются два распределения с далеко отстоящими средними значениями.

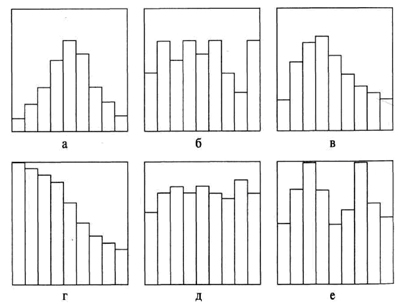
Рис. 3.3. Основные формы гистограмм:

а — симметричная, или колоколообразная;  б - гребенка'

в — положительно скошенное распределение;       г -  распределение с обрывом справа;

д — равномерное распределение (плато);    е -  двухпиковая (бимодальная) форма.

Этапы построения гистограммы

 

в таблице 1 приведены данные о росте студентов-юношей в отдельно выбранной студенческой группе.

На основании этих данных можно построить гистограмму, отражающую частоту появления того или иного значения в выборке, а также диапазон рассеивания значений (в данном случае - значений роста юношей).

Таблица 1

Исходные данные для построения гистограммы.

Студент	Рост, см
1	170
2	163
3	162
4	183
5	173
6	171
7	180
8	172
9	185
10	177
11	179
12	176
13	179
14	172
15	169
16	190

Для построения гистограммы нужно определить следующие параметры:

1. Граничные точки.

2. В нашем случае граничными точками будут значения 162 и 190 (минимальное и максимальное значения в выборке)

3. Количество классов гистограммы, определяется как корень квадратный из объема выборки. В нашем случае объем выборки равен шестнадцати, т.е. количество классов: sqrt (16) = 4

4. Ширина одного класса: расстояние между граничными точками нужно разделить на количество классов. В нашем случае ширина одного класса вычисляется как (190-162) / 4 =7

Теперь нужно определить границы каждого класса:

1-й класс: 162-168

2-й класс: 169-175

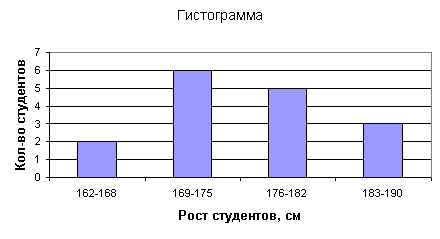
3-й класс: 176-182

4-й класс: 183-190

После того, как мы нанесли <сетку> гистограммы на систему координат, нужно отметить количество событий из нашей выборки, попадающих в тот или иной класс.