
- •1. Матрицы. Линейные операции над ними и их свойства.
- •2. Умножение матриц. Транспонирование. Свойства.
- •3. Определители матриц. Свойства определителей. Миноры и алгебраические дополнения.
- •4. Обратная матрица. Достаточное условие существования обратной матрицы.
- •6. Решение линейных уравнений. Решение невырожденых систем.
- •8. Решение произвольных систем. Теорема Кронекера-Капелли.
- •9. Однородные система уравнений. Фундаментальная система решений.
- •11. Декартова и полярная система координат.
- •12.Скалярное произведение векторов и его свойства.
- •13. Прямая на плоскости. Виды уравнений прямой на плоскости. Угол между двумя прямыми.
- •14. Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями.
- •15. Прямая в пространстве. Виды уравнений прямой. Угол между прямыми.
- •21. Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства.
- •22, 23. Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису.
- •24.Собственные векторы и собственные значения
- •25. Приведение матрицы к диагональному виду
- •28. Критерий Сильвестра
- •29. Исследование кривой второго порядка по ее уравнению без произведения координат.
- •1. Определение предела числовой функции. Односторонние пределы. Свойства пределов.
- •3. Замечательные пределы.
- •4. Предел функции по Гейне
- •5.Предел функции на бесконечности
- •7. Замечательные пределы.
- •8.Эквивалентные бесконечно малые величины и их св-ва
- •9, 12. Непрерывные функции и их свойства.
- •10.Доказательство непрерывности элементарных функций.
- •11. Точка разрыва функций и их классификация.
- •20 Формула Тейлора с остаточным членом в форме
- •21. Разложение функций ex, cos X, sin X по формуле Маклорена
- •14. Дифференцируемость функции. Дифференциал.
- •15. Правила дифференцирования суммы, произведения, частного функции. Производные сложных функций.
- •16. Дифферинциал и его применение.
- •17. Дифференциалы высших порядков.
- •18. Рррррррррррррррр
- •19. Теоремы о среднем. Правило Лопиталя.
- •22. Экстремум функции (для одной переменной)
- •23.Направление выпуклости ф-ии (опр,признаки)
- •24. Асимптоты
14. Дифференцируемость функции. Дифференциал.
Производной функции y=f(x) в точке х0 называется предел отношения приращения функции к приращению аргумента, когда аргумент стремится к нулю.
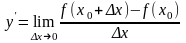
Производная функции f(x) есть некоторая функция
f ’(x), произведенная из данной функции.
Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале.
Операция нахождения производной называется дифференцированием.
Дифференциал функции y=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x) ).
Иначе. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
15. Правила дифференцирования суммы, произведения, частного функции. Производные сложных функций.
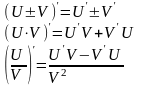
Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Производная обратной функции равна обратной величине производной данной функции.
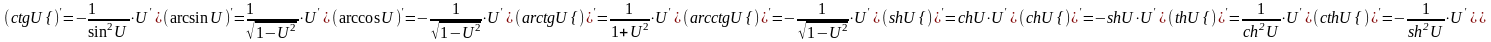
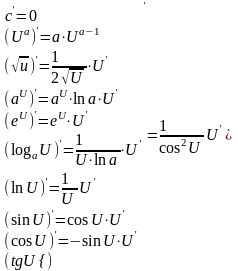
16. Дифферинциал и его применение.
Дифференциал функции y=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x) ).
Иначе. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Дифференциал первого порядка обладает свойством инвариантности формы при замене независимой переменной
Доказательство: y= f(x) dy= f’(x) dx x=j(t) dx=j’(t)dt y= f(j(t)) dy= (f(j)))’dt= f’(j(t))*j(t) dt = f’(x) dx
Смысл Физический смысл дифференциала: x=x(t) dx= x(t) dt= u (мгновенное) Физич. диф.- это путь, который прошла бы точка, если ее движение стало бы равномерным со скоростью, взятой в момент времени t Геометрический смысл дифференциала: Геометрически дифференциал равен приращению ординаты вдоль касательной к графику функции, проведенной в заданной точке.
17. Дифференциалы высших порядков.
Пусть y=f(x) дифференцируема функция, а ее аргумент х – независимая переменная. Тогда дифференциал dy=f ′(x)dx есть также функция х, можно найти дифференциал этой функции. Дифференциал от дифференциала есть второй дифференциал.
Производную можно рассматривать, как отношение дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.
Д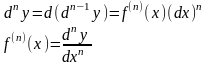 ифференциал
n-ого
порядка, есть дифференциал от дифференциала
(n-1)-ого
порядка, т.е. производную функции можно
рассматривать, как отношение ее
дифференциала соответствующего порядка
к соответствующей степени дифференциала
независимой переменной.
ифференциал
n-ого
порядка, есть дифференциал от дифференциала
(n-1)-ого
порядка, т.е. производную функции можно
рассматривать, как отношение ее
дифференциала соответствующего порядка
к соответствующей степени дифференциала
независимой переменной.
18. Рррррррррррррррр
Теорема Ферма: Если функция у=f(х) имеет в точке х0 локальный экстремум и дифференцируема в этой точке, то ее производная f'(х0) равна нулю.
Док-во: Проведем его для случая максимума в точке х0. Пусть (х0-, х0+) - та окрестность, для точек которой выполняется неравенство
З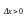
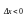
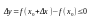 десь
возможно как 1 и 2 варианты, но | ∆х|
<δ
десь
возможно как 1 и 2 варианты, но | ∆х|
<δ
При ∆х>0, будет ∆y:∆x ≤0, поэтому
П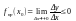 ри
∆х<0, будет ∆y:∆x
≥0, поэтому
ри
∆х<0, будет ∆y:∆x
≥0, поэтому
П о условию теоремы, существует производная f'(х0)А это означает, что правая производная fпр'(х0) и левая производная fл'(х0) равны между собой: fпр'(х0)= fл'(х0)= f'(х0). Таким образом, с одной стороны, f'(х0)≤0, с другой стороны, f'(х0)≥0, что возможно лишь, когда f'(х0)=0.
.Th Роля
Пусть ф-ция f(x) удовл. сл. усл.
А)Непрерывна на [a,b]
Б) Дифференц. на (a,b)
В) принимает на коцах отрезков равные значения f(a)=f(b), тогда на (a,b) т-ка такая что f‘(c)=0, т.е. с-крит. т-ка.
Док-во. Р-рим сначала, тривиальный случай, f(x) постоянная на [a,b] (f(a)=f(b)), тогда f‘(x)=0 x (a,b), любую т-ку можно взять в кач-ве с. Пусть f const на [a,b], т.к. она непрер. на этом отрезке, то по т-ме Вейерштрасса она достигает своего экстрем. на этом отрезке и max и min. Поскольку f принимает равные знач. в гранич. т-ках, то хотя бы 1- экстр. – max или min обязательно достигается во внутр. т-ке. с(a,b) (в противном случае f=const), то по т-ме Ферма, тогда f‘(c)=0, что и требовалось д-ть.
Th Логранжа (формула конечн.приращен)
Пусть ф-ция f(x) непрер. на отрезке [a,b] и диф. на интервале (a,b), тогда т. х и x+x [a,b] т-ка С лежащая между х и х+х такая что спаведлива ф-ла (f(x+x)-f(x))=f(c)x (7) => при сравнении с ф-лой приращения ф-ций с диф. заметим, что (7) явл. точной ф-лой, однако теперь пр-ная фолжна считаться в некоторой средней т-ке С «алгоритм» выбора которой неизвестен. Крайнее значение (a,b) не запрещены.
Придадим ф-ле (7) классический вид => x=a x+x=b+> тогда ф-ла (7)=(f(b)-f(a))/(b-a)=f‘(c) (7‘) – ф-ла конечных приращений Логранджа.
(f(b)-f(a))/(b-a)=f‘(c) (1)
Док-во сводится к сведению к т-ме Ролля. Р-рим вспом. ф-цию g(x)=f(x)-f(a)-(f(b)-f(a))/(b-a) (x-a)
Пусть ф-ция g(x) удовл. всем усл. т-мы Ролля на [a,b]
А)Непрерывна на [a,b]
Б) Дифференц. на (a,b)
В) g(a)=g(b)=0
Все усл. Ролля соблюдены, поэтому т-ка С на (a,b) g‘(c)=0 g‘(c)=f‘(x)-(f(b)-f(a))/(b-a). Ф-ла (1) наз-ся ф-лой конечных приращений.
.Th Коши(обобщенная формула конечн.приращен)
Теорема Коши: Пусть функции у=f(х) и у=g(х) неперырвны на отрезке [a,b],дифференцируемы хотя бы в открытом промежутке (a,b) и на этом промежутке g'(х) не обращается в нуль. Тогда существует такая точка c (a,b), что выполняется равенство (1)
Д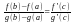 окозательство:
Вначале отметим, что знаменатель
g(b)-g(a)
≠ 0,т.к. из
равенства g(b)=g(a)
следовало бы по теореме Ролля, что
производная g'(х)
обратилась бы в нуль в какой-нибудь
точке промежутка (a,b),
что противоречит условию g'(х)≠0.
Образуем вспомогательную функцию:
окозательство:
Вначале отметим, что знаменатель
g(b)-g(a)
≠ 0,т.к. из
равенства g(b)=g(a)
следовало бы по теореме Ролля, что
производная g'(х)
обратилась бы в нуль в какой-нибудь
точке промежутка (a,b),
что противоречит условию g'(х)≠0.
Образуем вспомогательную функцию:
К ней применима теорема Ролля: F(х) непрерывна в [a,b] и дифференцируема в (a,b) как сумма функций, непрерывных и дифференцируемых в соответствующих промежутках, кроме того, как легко проверить непосредственно, F(a)=F(b)=0. Следовательно, существует точка c (a,b), , такая, что F'(c)=0. Вычисляем:
П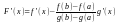 одставляем
x=c:
одставляем
x=c:

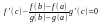
После деления на g'(х) (причем как говорилось раньше g'(х) 0), мы приходим к формуле (1)
