9, 12. Непрерывные функции и их свойства.
Пусть функция y=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке:
Это означает:
- функция определена в точке х0 и в ее окрестности;
- функция имеет предел при х→х0
- предел функции в точке х0 равен значению функции в этой точке, т.е. выполняется равенство.
Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х0
10.Доказательство непрерывности элементарных функций.
11. Точка разрыва функций и их классификация.
Точки разрыва функции – это точки в которых нарушается непрерывность функции.
Точка разрыва х0 называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)
и
При этом, если:
- А1=А2 то точка х0 называется точкой устранимого разрыва;
- А1≠А2 то точка х0 называется точкой конечного разрыва.
|A1 – A2| называется скачком функции.
Точка разрыва х0 называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности.
13. Производная. Ее геометрический и физический смысл.
Физический: производной функции y=f(x) в точке х0 называется предел отношения приращения функции ∆y в этой точке к вызвавшему его приращению аргумента ∆х при произвольном стремлении ∆х к 0.
Геометрический: угловой коэффициент касательной к графику функции в точке с абсциссой х0 равен значению производной этой функции в точке х0.
20 Формула Тейлора с остаточным членом в форме
Лагранжа.
Пусть функция f определена на отрезке [x0, x0 + ∆] (∆ > 0) и имеет там
непрерывную производную n-го порядка и, кроме того, по крайней мере на
интервале (x0, x0 + ∆) существует производная n + 1-го порядка (случай,
когда f задана на [x0 − ∆, x0] рассматривается аналогично). Положим
и, фиксировав x ∈ [x0, x0 +∆] , по образцу правой части (4) составим вспо-
могательную функцию
переменной z. На отрезке [x0, x] функция ϕ непрерывна,
и, кроме того, в интервале (x0, x) существует производная
Формула Тейлора с остаточным членом в форме Лагранжа имеет вид
21. Разложение функций ex, cos X, sin X по формуле Маклорена
Разложение функции ex
Так как (ex)' = ex, то производная любого порядка функции ex равна ex. При x = 0 функция ex и ее производные любого порядка равны одному. Таким образом, формула Маклорена для функции ex имеет вид
Отметим, что для
любого вещественного числа x остаточный
член
В самом деле, если x – фиксированное число, то, начиная с некоторого положительного целого числа N, для любого n > N имеем
Следовательно
так как q < 1, а
величина
является постоянной при любом n. Таким
образом, значения функции ex могут быть
найдены приближенно по формуле:
Разложение функции cos x
Находим последовательно производные от f(x) = cos x.
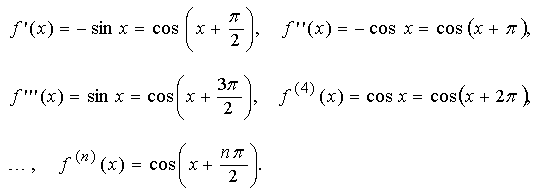
При x = 0 получаем
Следовательно, формула Маклорена для функции cos x имеет вид
Так как
, то
для любого фиксированного вещественного числа x. Таким образом, значения функции cosx могут быть найдены приближенно по формуле
Разложение функции sin x
Формула Маклорена для функции sin x находится аналогично формуле Маклорена для cos x
Причем
для любого фиксированного вещественного числа x.