20. Методика проверки гипотезы о законе распределения случайной величины. Методику пояснить на примере проверки гипотезы о законе нормального распределения случайной величины.

Проверка гипотезы о законе распределения случайной величины включает в себя выполнение следующих процедур:

1. Вычисление теоретических значений частот 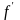, используя дифференциальную функцию предполагаемого закона распределения, параметры которого принимают равными статистическим параметрам выборки.

2. Построение по значениям статистических и теоретических частот графиков соответствующих распределений. Визуальная оценка близости эмпирического распределения к предполагаемому теоретическому закону.

3. Вычисление критерия согласия, оценивающего степень согласованности теоретического и статистического распределений.

4. Сопоставление расчетного значения критерия согласия с его табличным, называемым критическим значением. Принятие решения о достоверности гипотезы о законе распределения исследуемой случайной величины или отбрасывании ее, как противоречивой опытным данным.

1). Вычисление теоретических значений частот . Пусть по внешнему виду эмпирическая кривая распределения приближается к теоретической кривой нормального распределения. Тогда, согласно уравнению (9) плотности вероятности случайной величины непрерывного типа, подчиняющейся закону нормального распределения, можно считать, что 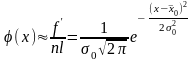. Следовательно, для i – го интервала размаха статистического распределения и условий 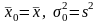имеем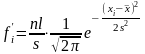 ,(11) где - теоретическая частота; n –объем выборки (объем эмпирической совокупности); l – величина единичного интервала эмпирической совокупности.

2) Оценка близости эмпирического распределения к предполагаемому теоретическому закону. На рис. 2 приведены полученные теоретическая и эмпирическая кривые распределения. Визуальный анализ результатов совмещения двух кривых распределения случайной величины x (отклонения от номинального размера диаметра роликов) позволяет заключить, что эмпирическое распределение может рассматриваться как распределение по нормальному закону.

3). Вычисление критерия согласия, оценивающего степень согласованности теоретического и статистического распределений. Для проверки гипотезы нормальности распределения генеральной совокупности по взятой из нее выборке можно использовать как критерий , так и критерий χ². Выполним проверку по обоим критериям. Проверка гипотезы нормальности распределения по критерию . Для определения значения критерия λ по формуле (5) вычислим значения эмпирической и теоретической функций нормального закона распределения и их разности для каждого наблюденного значения случайной величины х по формулам 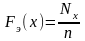; , в которых и - накопленные теоретические и эмпирические частоты; n - объем выборки. При этом считаем, что накопленной частотой любого m значения x_i является сумма частот всех предшествующих значений x_i, включая и частоту самого x_i , где m — число значений х_i; f_i - частота i-го значения х. Используя данные табл. 6 и 7, получим результаты вычисления , и . Максимальная разность этих функций составляет 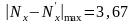. По формуле (5) получим 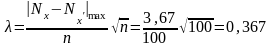. Этому значению  соответствует . Эта вероятность близка к единице. Поэтому можно нашу нулевую гипотезу считать верной. Проверка гипотезы нормальности распределения по критерию χ². Используя результаты вычисления теоретических и эмпирических частот и 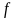(табл. 6, 7) вычислим критерий χ² по формуле . Результаты промежуточных вычислений критерия χ² приведены в табл. 9. Заметим, что поскольку частоты 1 и 7-го интервалов менее 5, то они объединены с соседними интервалами. По табл. 9 имеем 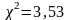. Число степеней k = т – р - 1 = 5 – 2 - 1 = 2, где m = 5 – число разрядов, р = 2 – число параметров закона распределения. . 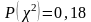Эта вероятность больше уровня значимости q = 0,05, следовательно, и по критерию χ² нашу нулевую гипотезу можно считать верной.