
- •Числовые характеристики рассеивания значений случайной величины. Основные свойства математического ожидания и дисперсии.
- •Данные для вычисления критерия
- •Методика проверки гипотезы о законе распределения случайной величины. Методику пояснить на примере проверки гипотезы о законе нормального распределения случайной величины.
- •Методика проверки гипотезы случайности выборки способом последовательных разностей. Определение расчетного и критического значений критерия .
- •Методика проверки гипотезы случайности выборки способом длины и числа серий. Условия принятия гипотезы о случайности выборки.
- •Методика проверки гипотезы равенства двух выборочных средних для выборок, взятых из нормальной генеральной совокупности, с использованием критерия Стьюдента.
- •Методика проверка гипотезы равенства двух выборочных дисперсий для выборок, взятых из нормальной генеральной совокупности. Как определяется расчетное и критическое значения критерия т?
- •Методика проверки гипотезы однородности ряда дисперсий при равном объеме выборок, взятых из нормальной генеральной совокупности. Как определяется расчетное и критическое значения критерия g?
Случайное событие, несовместные и независимые события. События невозможные и достоверные. Вероятность, частота и частость события, свойства вероятностей. Правила сложения и умножения вероятностей. Сущность закона больших чисел.
Если
в испытаниях может произойти либо
событие
А,
либо
В,
либо
С
и т. д., то такие события называются
возможными
или
случайными.
Следовательно,
случайным называется
такое событие, которое при испытании
может либо наступить,
либо не наступить. Извлечение дефектных
деталей. Под
несовместимыми
понимаются
такие события, которые не могут
появляться вместе, одновременно. Под
независимыми
событиями
понимаются такие, появление которых не
зависит от того, какое
событие произошло перед этим. Если
при каждом испытании
неизбежно происходит событие А,
то
такое событие называется достоверным.
Если
в условиях данного испытания некоторое
событие В
заведомо
не может произойти, то оно называется
невозможным.
Для
количественной
оценки возможности осуществления
случайного события пользуются термином
вероятность.
Вероятность
какого-либо события А
обозначается
символом Р(А)
и представляет собой численную меру
объективной возможности
этого события. В
качестве такой единицы измерения принята
вероятность
достоверного события,
равная единице.
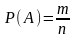 число
случаев т,
благоприятствующих
этому событию, к числу п
всех
возможных случаев данного
класса испытаний. На
практике не всегда выполняются условия
вероятности. При
изучении массовых явлений какое-либо
случайное событие или
случайная величина могут появляться
несколько раз в процессе
испытаний. Например, пусть при N
испытаниях
событие А
фактически
появилось f
раз. Число f
носит название частоты
появления события А.
Отношение
частоты события А
к
общему
числу
испытаний N
носит
название частости
события или
относительной
частоты,
которую
будем обозначать тА:
число
случаев т,
благоприятствующих
этому событию, к числу п
всех
возможных случаев данного
класса испытаний. На
практике не всегда выполняются условия
вероятности. При
изучении массовых явлений какое-либо
случайное событие или
случайная величина могут появляться
несколько раз в процессе
испытаний. Например, пусть при N
испытаниях
событие А
фактически
появилось f
раз. Число f
носит название частоты
появления события А.
Отношение
частоты события А
к
общему
числу
испытаний N
носит
название частости
события или
относительной
частоты,
которую
будем обозначать тА:
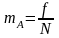
Основные свойства вероятностей.
1
Вероятность
достоверного события А1
равна
единице: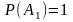 .
Так
как число случаев m,
благоприятствующих достоверному
событию,
равно числу всех возможных случаев п,
т.
е. т
= п;
следовательно,
.
Так
как число случаев m,
благоприятствующих достоверному
событию,
равно числу всех возможных случаев п,
т.
е. т
= п;
следовательно,
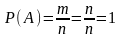 .
.
2
Вероятность
невозможного события А2
равна
нулю P(A2)=0,так
как невозможному событию не благоприятствует
ни один из n
возможных
случаев, т. е. т
= 0,
и, следовательно,
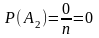 .
.
3
Вероятность
случайного события А3
заключена между нулем и
единицей, так как в этом случае 0 < m
< п,
а
значит
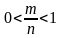 ;
следовательно, 0 < Р(A3)<1.
Вероятность любого события
А
определяется
неравенством 0
<
Р(А)<
1.
Правило
сложения вероятностей. Вероятности
случайных событий
или величин можно складывать и умножать.
Если события А,
В
и
С
несовместимы,
т. е. появление любого из них исключает
возможность
появления другого и вероятность появления
каждого соответственно равна Р(А),
Р(В),
Р(С),
то
вероятность осуществления
какого-либо из этих несовместимых
событий (A
или В
или
С)
равна сумме их вероятностей, т. е. Р(А
или
В
или
С)
= Р(А)
+ Р(B)
+ Р(С).
;
следовательно, 0 < Р(A3)<1.
Вероятность любого события
А
определяется
неравенством 0
<
Р(А)<
1.
Правило
сложения вероятностей. Вероятности
случайных событий
или величин можно складывать и умножать.
Если события А,
В
и
С
несовместимы,
т. е. появление любого из них исключает
возможность
появления другого и вероятность появления
каждого соответственно равна Р(А),
Р(В),
Р(С),
то
вероятность осуществления
какого-либо из этих несовместимых
событий (A
или В
или
С)
равна сумме их вероятностей, т. е. Р(А
или
В
или
С)
= Р(А)
+ Р(B)
+ Р(С).
Из правила сложения вероятностей вытекают два следствия:
1. Сумма вероятностей противоположных событий равна единице. Если обозначим вероятность осуществления какого-либо события через р, а вероятность его неосуществления через q, то р + q=1,
так как достоверно, что оно либо осуществится, либо нет.
2. Вероятность противоположного события равна дополнению до единицы к вероятности данного события, т. е. q = 1 – p.
Правило умножения вероятностей. Если события A и B зависимы, то вероятность появления события B, вычисленная в предположении, что событие A наступило, называется условной вероятностью события B обозначается символом P(B/A). Для зависимых событий правило умножения вероятностей может быть сформулировано следующим образом: вероятность появления нескольких зависимых событий A, В и С одновременно равна произведению их вероятностей, вычисленных для каждого из них в предположении, что предшествующие ему события имели место, т. е. Р(А и В и С) = Р(А)×Р(В/А)×Р(С/АВ). Для независимых событий правило умножения вероятностей является следствием предыдущего правила. Для независимых событий условная вероятность равна безусловной вероятности: т. е. P(B/A) = P(B), поэтому вероятность появления нескольких независимых событий равна произведению их вероятностей: P(A и B и C) = P(A)×P(B)×P(C).
Закон
больших чисел. Из
статистического определения вероятности
можно сделать вывод, что между вероятностью
и частостью какого-либо события существует
приближенное равенство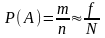 ,которое
будет тем точнее, чем больше число
испытаний. Теорема Я. Бернулли гласит,
что с вероятностью, как угодно близкой
к достоверности, можно утверждать, что
при достаточно
большом
числе испытаний N
частость
,которое
будет тем точнее, чем больше число
испытаний. Теорема Я. Бернулли гласит,
что с вероятностью, как угодно близкой
к достоверности, можно утверждать, что
при достаточно
большом
числе испытаний N
частость
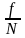 появления события А,
имеющего
во всех испытаниях постоянную вероятность
р,
будет
как угодно мало отличаться от этой
вероятности, т. е.
появления события А,
имеющего
во всех испытаниях постоянную вероятность
р,
будет
как угодно мало отличаться от этой
вероятности, т. е.
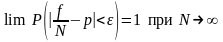 ,
где ε — как угодно малое положительное
число.
,
где ε — как угодно малое положительное
число.
Случайная величина. Дискретные и непрерывные случайные величины. Примеры параметров процессов механической обработки деталей, являющиеся случайными величинами. Как осуществляют оценку возможности случайной величины принимать те или иные значения?
Что понимают под распределением случайной величины? Теоретические и эмпирические распределения случайной величины. Функция распределения и плотность вероятности случайной величины.
Случайной величиной называется переменная величина, которая в результате испытаний (опытов) может принять то или иное значение в границах определенного интервала. Например, действительный размер детали, обработанной на станке, является случайной величиной, так как он может принять любое численное значение в определенных пределах. Дискретными случайными величинами называются такие, которые в результате испытаний могут принимать лишь отдельные, изолированные, большей частью целочисленные значения, и не могут принимать значения, промежуточные между ними. Например, количество негодных деталей в партии. Непрерывной случайной величиной называется такая, которая в результате испытаний может принимать любые численные значения из непрерывного ряда их возможных значений в границах определенного интервала. Например, действительные размеры деталей. Возможности случайных величин принимать при испытаниях те или иные численные значения оцениваются при помощи вероятностей. Совокупность значений случайных величин, расположенных в возрастающем порядке с указанием их вероятностей, называется распределением случайных величин. Различают теоретические и эмпирические распределения случайных величин. В теоретических распределениях оценка возможных значений случайной величины производится при помощи вероятностей, а в эмпирических — при помощи частот или частостей, полученных в результате опытов или испытаний. Следовательно, эмпирическим распределением случайной величины называется совокупность наблюденных значений ее, расположенных в возрастающем порядке, с указанием соответствующих частот или частостей. Распределения случайных величин дискретного типа можно представить в виде табл. или графика (рис. 1).
 Если
случайная величина является непрерывной,
то возникает затруднение представить
ее распределение в виде таблицы или
графика, даже если значения случайной
величины лежат в весьма узком интервале.
Поэтому на практике при изучении
случайных величин непрерывного типа
их полученные значения разбивают на
интервалы (разряды) с таким расчетом,
чтобы величина интервала была несколько
больше цены деления шкалы измерительного
инструмента и таким образом компенсировалась
бы погрешность измерений. Затем
подсчитывают частоты не по действительным
значениям случайной величины, а по
интервалам, т. е. имеют дело не с частотами
наблюденных значений случайной величины
непрерывного типа, а с частотами их
значений, лежащих в границах установленного
интервала.
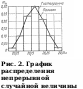
Эмпирическое
распределение случайной величины
непрерывного типа может быть представлено
в виде ступенчатого графика или в виде
ломаной кривой (рис. 2). Ступенчатый
график называется
гистограммой распределения,
а ломаная кривая —
полигоном распределения
или
эмпирической кривой распределения.
Если
случайная величина является непрерывной,
то возникает затруднение представить
ее распределение в виде таблицы или
графика, даже если значения случайной
величины лежат в весьма узком интервале.
Поэтому на практике при изучении
случайных величин непрерывного типа
их полученные значения разбивают на
интервалы (разряды) с таким расчетом,
чтобы величина интервала была несколько
больше цены деления шкалы измерительного
инструмента и таким образом компенсировалась
бы погрешность измерений. Затем
подсчитывают частоты не по действительным
значениям случайной величины, а по
интервалам, т. е. имеют дело не с частотами
наблюденных значений случайной величины
непрерывного типа, а с частотами их
значений, лежащих в границах установленного
интервала.
Эмпирическое
распределение случайной величины
непрерывного типа может быть представлено
в виде ступенчатого графика или в виде
ломаной кривой (рис. 2). Ступенчатый
график называется
гистограммой распределения,
а ломаная кривая —
полигоном распределения
или
эмпирической кривой распределения.
Функции распределения. Пусть X — случайная величина, а x — какое-либо действительное число: при этом X < x и этому событию отвечает вероятность P(X < x), которая, очевидно, является функцией х, т.е. P(X < x) = F(x); F(x) называется функцией распределения вероятностей случайной величины или интегральной функцией распределения. Таким образом, интегральная функция распределения определяет вероятность того, что случайная величина X при испытаниях примет значение меньше произвольно изменяемого действительного числа x (- ∞ < x < + ∞). Случайная величина считается заданной, если известна ее функция распределения. Для дискретной случайной величины интегральная функция распределения F(x) легко определяется по таблице или графику распределения. Интегральную функцию распределения можно представить в виде графика, если по оси абсцисс откладывать значения х, а по оси ординат — значения F(x) = P(X < x).
И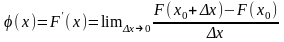 нтегральная
функция распределения непрерывной
случайной величины является дифференцируемой
функцией. Первая производная от
интегральной функции называется
дифференциальной
функцией распределения,
или
плотностью вероятности.
нтегральная
функция распределения непрерывной
случайной величины является дифференцируемой
функцией. Первая производная от
интегральной функции называется
дифференциальной
функцией распределения,
или
плотностью вероятности.
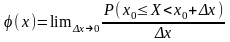
Т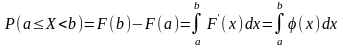 аким
образом, плотность вероятности φ(x)
есть предел отношения вероятности того,
что случайная величина X
при испытаниях примет значение, лежащее
в границах от
x0
до
x0
+ Δx
к
величине интервала
Δx,
когда величина
Δx
стремится к нулю. F(x)
является первообразной функцией по
отношению к φ(x),
поэтому
вероятность того, что случайная величина
X
при испытаниях примет значение, лежащее
в границах от
a
до
b,
равна определенному интегралу в пределах
от
a
до
b
от плотности вероятности:
аким
образом, плотность вероятности φ(x)
есть предел отношения вероятности того,
что случайная величина X
при испытаниях примет значение, лежащее
в границах от
x0
до
x0
+ Δx
к
величине интервала
Δx,
когда величина
Δx
стремится к нулю. F(x)
является первообразной функцией по
отношению к φ(x),
поэтому
вероятность того, что случайная величина
X
при испытаниях примет значение, лежащее
в границах от
a
до
b,
равна определенному интегралу в пределах
от
a
до
b
от плотности вероятности:
Числовые характеристики положения центра группирования значений случайных величин: математическое ожидание, среднее арифметическое значение, медиана и мода случайной величины.
Ч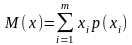 исловые
характеристики положения центра
группирования носят общее название мер
положения,
а числовые характеристики рассеивания
—
мер
рассеивания.
Математическим
ожиданием
M(x)
дискретной случайной величины x
называется сумма произведений всех m
ее возможных значений xi
на их вероятности p(xi)
исловые
характеристики положения центра
группирования носят общее название мер
положения,
а числовые характеристики рассеивания
—
мер
рассеивания.
Математическим
ожиданием
M(x)
дискретной случайной величины x
называется сумма произведений всех m
ее возможных значений xi
на их вероятности p(xi)
Д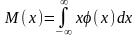 ля
непрерывной случайной величины ее
математическое ожидание M(x)
определяется по формуле
ля
непрерывной случайной величины ее
математическое ожидание M(x)
определяется по формуле
где φ(x) плотность вероятностей величины x.
М
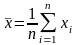 атематическое
ожидание обычно используется в качестве
меры положения для теоретических
распределений (где используется так
называемая генеральная
совокупность
объектов), в которых возможные значения
x
оцениваются при помощи вероятностей.
В эмпирических распределениях, где
наблюденные значения x
оцениваются при помощи частот или
частостей, в качестве меры положения
используется среднее арифметическое
атематическое
ожидание обычно используется в качестве
меры положения для теоретических
распределений (где используется так
называемая генеральная
совокупность
объектов), в которых возможные значения
x
оцениваются при помощи вероятностей.
В эмпирических распределениях, где
наблюденные значения x
оцениваются при помощи частот или
частостей, в качестве меры положения
используется среднее арифметическое
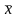 .
Среднее
арифметическое значение
случайной величины x.
При большом числе n
полагают, что среднее арифметическое
значение случайной величины x
приближенно равно ее математическому
ожиданию:
.
Среднее
арифметическое значение
случайной величины x.
При большом числе n
полагают, что среднее арифметическое
значение случайной величины x
приближенно равно ее математическому
ожиданию:
С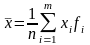 реднее
арифметическое значение
случайной
величины может быть вычислена как сумма
произведений наблюденных значений
случайной величины на их частости:
где
fi
- частота значений xi;
n
- общее число наблюденных значений xi,
реднее
арифметическое значение
случайной
величины может быть вычислена как сумма
произведений наблюденных значений
случайной величины на их частости:
где
fi
- частота значений xi;
n
- общее число наблюденных значений xi,
 ;
m
- число отдельных значений
xi.Для
непрерывных случайных величин в качестве
xi
принимают середину интервалов, на
которые разбивается наблюденный ряд
значений x.
;
m
- число отдельных значений
xi.Для
непрерывных случайных величин в качестве
xi
принимают середину интервалов, на
которые разбивается наблюденный ряд
значений x.
О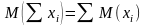 сновные
свойства
математического ожидания. 1
Математическое ожидание постоянной
C
есть сама эта постоянная: М(C)
= С.
2
Математическое ожидание произведения
постоянной величины С
на случайную величину
х
равно произведению постоянной на
математическое ожидание случайной
величины: M(Cx)
= CM(x).
3
Математическое ожидание суммы нескольких
случайных величин равно сумме
математических ожиданий этих величин:
сновные
свойства
математического ожидания. 1
Математическое ожидание постоянной
C
есть сама эта постоянная: М(C)
= С.
2
Математическое ожидание произведения
постоянной величины С
на случайную величину
х
равно произведению постоянной на
математическое ожидание случайной
величины: M(Cx)
= CM(x).
3
Математическое ожидание суммы нескольких
случайных величин равно сумме
математических ожиданий этих величин:
4 Математическое ожидание суммы постоянной и случайной величины равно сумме постоянной величины и математического ожидания случайной величины: M(C + x) = C + M(x). 5 Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M(xy) = M(x)·M(y).
 М
М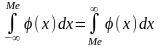 едианой
непрерывной случайной величины называется
такое ее значение, для которой функция
распределения равна 0,5. Это означает,
что вероятность случайной величины
х
принять значение, меньшее медианы, в
точности равна вероятности этой величины
принять значение, большее медианы.
Медиана обозначается символом
Me
и для непрерывной случайной величины
определяется из соотношения.
едианой
непрерывной случайной величины называется
такое ее значение, для которой функция
распределения равна 0,5. Это означает,
что вероятность случайной величины
х
принять значение, меньшее медианы, в
точности равна вероятности этой величины
принять значение, большее медианы.
Медиана обозначается символом
Me
и для непрерывной случайной величины
определяется из соотношения.
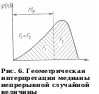
Геометрически медиана является абсциссой такой точки кривой плотности вероятности φ(х), ордината которой делит площадь под кривой на две равновеликие части (рис. 6).
Если случайная величина x дискретного типа, то для определения медианы значения х располагают в порядке возрастания их величин (x1, x2, x3,…, xm,…, xn) и в качестве медианы принимают такое срединное значение x между xm-1 и xm, чтобы удовлетворялось условие
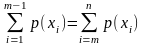
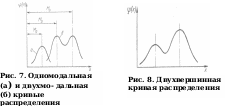
Модой Mo называется такое значение случайной величины x, которое имеет наибольшую вероятность p(x) для распределения дискретной случайной величины или наибольшую плотность вероятности φ(x) для распределения непрерывной случайной величины. Если кривая распределения имеет два или несколько одинаковых максимумов, то она называется соответственно двухмодальной или многомодальной (рис. 7). Если максимумы резко выражены, но различны по величине, то кривая называется многовершинной (рис. 8). Если в центральной части кривой распределения имеется минимум, по обе стороны от которого происходит непрерывное возрастание кривой до границ области значений случайной величины, то такая кривая называется антимодальной (рис. 9).

Числовые характеристики рассеивания значений случайной величины. Основные свойства математического ожидания и дисперсии.
В
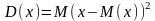 технике наиболее употребительными
мерами рассеивания являются: дисперсия,
обозначаемая символами D(x),
σ2
или
s2,
среднее квадратическое отклонение,
обозначаемое через символы σ
или
s,
и размах, обозначаемой символом R.
Дисперсией
(рассеянием)
возможных значений xi
случайной величины x
около ее математического ожидания M(x)
называют математическое ожидание
квадрата отклонения случайной величины
от ее математического ожидания. Дисперсия
дискретной случайной величины
непосредственно вычисляется по формуле
технике наиболее употребительными
мерами рассеивания являются: дисперсия,
обозначаемая символами D(x),
σ2
или
s2,
среднее квадратическое отклонение,
обозначаемое через символы σ
или
s,
и размах, обозначаемой символом R.
Дисперсией
(рассеянием)
возможных значений xi
случайной величины x
около ее математического ожидания M(x)
называют математическое ожидание
квадрата отклонения случайной величины
от ее математического ожидания. Дисперсия
дискретной случайной величины
непосредственно вычисляется по формуле
.
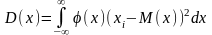
Для непрерывной случайной величины дисперсия определяется по формуле
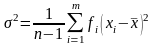
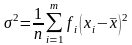
Для эмпирического распределения дисперсию обозначают через σ2 или s2 и определяют по формуле: при n > 30 при n < 30
Д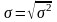
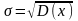 исперсия
имеет размерность, представляющую собой
квадрат размерности самой случайной
величины. На практике это неудобно.
Поэтому в технике чаще пользуются не
самой дисперсией, а корнем квадратным
из нее, взятым со знаком плюс и называемым
средним
квадратическим отклонением:
или
для эмпирических распределений
исперсия
имеет размерность, представляющую собой
квадрат размерности самой случайной
величины. На практике это неудобно.
Поэтому в технике чаще пользуются не
самой дисперсией, а корнем квадратным
из нее, взятым со знаком плюс и называемым
средним
квадратическим отклонением:
или
для эмпирических распределений
Р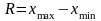 азмерность
σ совпадает с размерностью самой
случайной величины
х.
Размахом, или широтой распределения
пользуются как мерой рассеивания в
эмпирических распределениях при малом
числе наблюдений, когда
п < 10.
Размахом
называется разность между наибольшим
и наименьшим наблюденными значениями
случайной величины:
азмерность
σ совпадает с размерностью самой
случайной величины
х.
Размахом, или широтой распределения
пользуются как мерой рассеивания в
эмпирических распределениях при малом
числе наблюдений, когда
п < 10.
Размахом
называется разность между наибольшим
и наименьшим наблюденными значениями
случайной величины:
Основные свойства дисперсий и средних квадратических отклонений. Дисперсии и средние квадратические отклонения обладают рядом свойств, вытекающих из теорем о дисперсиях. Приводим эти свойства без доказательств.
1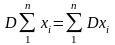 Дисперсия постоянной величины
с
равна нулю: Dc
= 0
2
Дисперсия произведения постоянной
величины
с
на случайную величину
х
равна
произведению квадрата постоянной
величины
с
на дисперсию случайной величины
х:
Dcx
=
c2Dx
3
Дисперсия
суммы постояной
c
и случайной величины
x
равна
дисперсии случайной величины
x:
D(c
+
x)
= Dx
4
Дисперсия
суммы нескольких независимых случайных
величин
х1,
х2,-
, хn
равна сумме дисперсий этих величин:
Дисперсия постоянной величины
с
равна нулю: Dc
= 0
2
Дисперсия произведения постоянной
величины
с
на случайную величину
х
равна
произведению квадрата постоянной
величины
с
на дисперсию случайной величины
х:
Dcx
=
c2Dx
3
Дисперсия
суммы постояной
c
и случайной величины
x
равна
дисперсии случайной величины
x:
D(c
+
x)
= Dx
4
Дисперсия
суммы нескольких независимых случайных
величин
х1,
х2,-
, хn
равна сумме дисперсий этих величин:
Закон биноминального распределения случайных величин. Уравнения и параметры этого закона распределения. Случайные величины процессов механической обработки и качества деталей, распределение которых может быть описано законом биноминального распределения.
Закон биноминального распределения используется при оценке качества и надежности изделий. Пусть производится серия последовательных независимых испытаний, каждое из которых заканчивается одним из двух несовместимых между собой результатов: или событие A наступает, или оно не наступает. Вероятность появления события A в каждом испытании равна р, а вероятность непоявления события A равна q = 1 - p. Так как испытания независимы, то вероятность появления или непоявления события A не зависит от результатов предыдущих испытаний. При такой схеме испытаний вероятность появления события A заданное число раз подчиняется закону биномиального распределения, который можно сформулировать так: если вероятность события A постоянна в серии последовательных независимых испытаний и равна p, то вероятность появления события A ровно k раз в п испытаниях будет равна
Э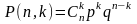 то
уравнение определяет собой распределение
вероятностей случайного числа k,
которое называется
биномиальным.
то
уравнение определяет собой распределение
вероятностей случайного числа k,
которое называется
биномиальным.
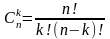 Символ
Символ
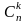 обозначает число сочетаний из n
элементов
по
k,
т. е. биномиальный
коэффициент.
обозначает число сочетаний из n
элементов
по
k,
т. е. биномиальный
коэффициент.
где символ n! обозначает факториал и выражает произведение натуральных чисел 1, 2, 3,. . ., n. При этом 0! = 1. С учетом изложенного формула (1) примет вид:
М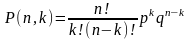 атематическое
ожидание
M(k)
и дисперсия
атематическое
ожидание
M(k)
и дисперсия
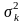 биномиального распределения равны:
M(k)
= np;
= npk.
биномиального распределения равны:
M(k)
= np;
= npk.
П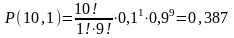 ример
1.
В партии деталей имеется брак, доля
которого составляет 0,1. Производится
последовательное извлечение 10 деталей.
После каждого извлечения и обследования
детали она вновь возвращается в партию,
которая затем тщательно перемешивается,
т.е. испытания носят независимый характер.
Какова вероятность того, что при
извлечении по такой схеме 10 деталей
среди них появится одна бракованная?
Очевидно, что вероятность извлечения
бракованной детали составляет
p
=
0,1, вероятность противоположного события
- извлечение годной детали q
= 1 - p
= 0,9. Число испытаний
n
= 10 и
k
=
1
ример
1.
В партии деталей имеется брак, доля
которого составляет 0,1. Производится
последовательное извлечение 10 деталей.
После каждого извлечения и обследования
детали она вновь возвращается в партию,
которая затем тщательно перемешивается,
т.е. испытания носят независимый характер.
Какова вероятность того, что при
извлечении по такой схеме 10 деталей
среди них появится одна бракованная?
Очевидно, что вероятность извлечения
бракованной детали составляет
p
=
0,1, вероятность противоположного события
- извлечение годной детали q
= 1 - p
= 0,9. Число испытаний
n
= 10 и
k
=
1
Полученный результат можно отнести и к тому случаю, когда извлекается подряд 10 деталей без возврата их обратно в партию, но объем партии достаточно велик. При достаточно большой партии, например 1000 шт., вероятность извлечения годной или негодной детали после каждого из 10 извлечений деталей изменится ничтожно мало. Поэтому при таких условиях извлечение бракованной детали можно рассматривать как событие, не зависящее от результатов предшествующих испытаний. Пример 2. На участке имеется пять одинаковых станков, коэффициент использования которых по времени составляет 0,8. Какова вероятность того, что в середине смены при нормальном ходе производства из пяти таких станков будет работать только два, а три не работать? Здесь p = 0,8; q = 0,2; n = 5 и k = 2:
.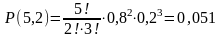
Закон редких событий (Пуассона) распределения случайных величин. Уравнения и параметры этого закона распределения. Случайные величины процессов механической обработки и качества деталей, распределение которых может быть описано законами биноминального и редких событий.
Если вероятность p события A очень мала (p ≤ 0,1), а число n испытаний велико, то вероятность того, что событие A наступит k раз в n испытаниях, будет равна
г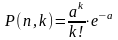 де
а = np
= M(k)
— математическое ожидание числа
k.
де
а = np
= M(k)
— математическое ожидание числа
k.
Уравнение определяет собой распределение редких событий, или распределение Пуассона.
К огда
число испытаний
n
велико, а
p
мало, то закон биномиального распределения
и закон редких событий практически
совпадают. Это имеет место тогда, когда
p
≤ 0,1 и
np
< 4. При этих условиях вместо формулы
можно применить формулу, т. е.
огда
число испытаний
n
велико, а
p
мало, то закон биномиального распределения
и закон редких событий практически
совпадают. Это имеет место тогда, когда
p
≤ 0,1 и
np
< 4. При этих условиях вместо формулы
можно применить формулу, т. е.
Принимая во внимание, что a = np , формула примет вид
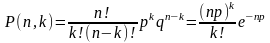
Распределение Пуассона имеет только один параметр а = np = Мk. Для этого распределения дисперсия численно равна математическому ожиданию: = M(k).
Поэтому, когда в распределении дискретной случайной величины и σ2 мало отличаются друг от друга по своим численным значениям, то можно уверенно считать, что данное распределение подчиняется закону редких событий. Закон редких событий имеет практическое применение в машиностроении для выборочного контроля готовой продукции, когда по техническим условиям в принимаемой партии продукции допускается некоторый процент брака (обычно небольшой) и поэтому всегда p << 0,1, а объем выборки n берут таким, чтобы было np << 4. При помощи закона редких событий можно вычислить вероятность того, что в выборке из n шт. будет содержаться: 0, 1, 2, 3 и т. д. бракованных деталей, т. е. заданное число k раз. Можно также вычислить вероятность появления в такой выборке k штук дефектных деталей и более. Эта вероятность на основании правила сложения вероятностей будет равна

где k = 0,1,2,...,l.
Если эта вероятность для некоторого значения k окажется очень малой (например, меньше 0,05), то на основании принципа практической невозможности маловероятных событий можно считать, что появление в выборке из n штук деталей k или более дефектных несовместимо с нашим исходным допущением, что во всей партии имеется не более 100р % брака. Следовательно, в действительности во всей партии имеется брак более чем 100р %, и она не может быть принята.
Закон нормального распределения случайных величин, уравнение и параметры этого закона. Случайные величины процессов механической обработки и качества деталей, распределение которых может быть описано законом нормального распределения.
З
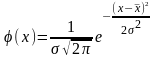 акон
нормального распределения находит
большое применение в различных отраслях
техники. Этому закону подчиняются,
многие непрерывные случайные величины,
встречающиеся в технике, например ошибки
измерения, высота микронеровностей на
обработанной поверхности и многие
другие.
Если
случайная величина X
представляет сумму очень большого числа
взаимно независимых случайных величин
x1,
x2,…,
xn,
влияние каждой из которых на всю сумму
ничтожно мало, то независимо от того,
каким законам распределения подчиняются
слагаемые
x1,
x2,…,
xn,
сама величина X
будет иметь распределение вероятностей,
близкое к нормальному, и тем точнее, чем
больше число слагаемых.
Теорема
Ляпунова дает теоретическое объяснение
и тому факту, что при устойчивом процессе
обработки деталей на настроенных станках
и при отсутствии изменяющихся во времени
систематических погрешностей
действительные размеры деталей часто
подчиняются закону нормального
распределения. Это объясняется тем, что
результирующая погрешность обработки
представляет собой сумму большого числа
погрешностей, зависящих от станка,
приспособления, инструмента и заготовки.
Плотность вероятности или дифференциальная
функция распределения случайной величины
непрерывного типа, подчиняющейся закону
нормального распределения, имеет
следующее выражение:
акон
нормального распределения находит
большое применение в различных отраслях
техники. Этому закону подчиняются,
многие непрерывные случайные величины,
встречающиеся в технике, например ошибки
измерения, высота микронеровностей на
обработанной поверхности и многие
другие.
Если
случайная величина X
представляет сумму очень большого числа
взаимно независимых случайных величин
x1,
x2,…,
xn,
влияние каждой из которых на всю сумму
ничтожно мало, то независимо от того,
каким законам распределения подчиняются
слагаемые
x1,
x2,…,
xn,
сама величина X
будет иметь распределение вероятностей,
близкое к нормальному, и тем точнее, чем
больше число слагаемых.
Теорема
Ляпунова дает теоретическое объяснение
и тому факту, что при устойчивом процессе
обработки деталей на настроенных станках
и при отсутствии изменяющихся во времени
систематических погрешностей
действительные размеры деталей часто
подчиняются закону нормального
распределения. Это объясняется тем, что
результирующая погрешность обработки
представляет собой сумму большого числа
погрешностей, зависящих от станка,
приспособления, инструмента и заготовки.
Плотность вероятности или дифференциальная
функция распределения случайной величины
непрерывного типа, подчиняющейся закону
нормального распределения, имеет
следующее выражение:
где x - переменная случайная величина;
φ(x)- плотность вероятности;
σ- среднее квадратическое отклонение случайной величины x от ;
- среднее значение (математическое ожидание) величин x;
e- основание натуральных логарифмов, e = 2,71828.
Дифференциальная функция нормального распределения графически выражается в виде кривой холмообразного типа (рис. 1). Из вида кривой нормального распределения следует, что она симметрична относительно ординаты точки x = , т. е. равновозможны одинаковые положительные и отрицательные отклонения от . При этом меньшие отклонения более вероятны, чем большие, и весьма большие отклонения от центра группирования маловероятны.
П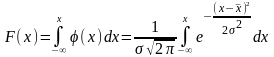 оложение
кривой относительно начала координат
и ее форма определяются двумя параметрами
и σ. С изменением
форма кривой не изменяется, но изменяется
ее положение относительно начала
координат (рис. 2). С изменением σ
положение кривой не изменяется, но
изменяется ее форма. С уменьшением σ
кривая становится более вытянутой, а
ветви ее сближаются; с увеличением
σ, наоборот,
кривая становится более приплюснутой,
а ветви ее раздвигаются шире. Интегральный
закон нормального распределения
выражается в общем виде так:
оложение
кривой относительно начала координат
и ее форма определяются двумя параметрами
и σ. С изменением
форма кривой не изменяется, но изменяется
ее положение относительно начала
координат (рис. 2). С изменением σ
положение кривой не изменяется, но
изменяется ее форма. С уменьшением σ
кривая становится более вытянутой, а
ветви ее сближаются; с увеличением
σ, наоборот,
кривая становится более приплюснутой,
а ветви ее раздвигаются шире. Интегральный
закон нормального распределения
выражается в общем виде так:
Законы равной вероятности и эксцентриситета (Релея) распределения случайных величин. Уравнения и параметры этих законов распределения. Случайные величины процессов механической обработки и качества деталей, распределение которых может быть описано законами равной вероятности и эксцентриситета.
Если непрерывная случайная величина x при испытаниях принимает все значения интервала (a, b) с одинаковой плотностью вероятности, то распределение плотности вероятности графически будет выражаться в виде прямоугольника с основанием ab и высотой φ(x) = const (рис. 6). Такой закон распределения непрерывной случайной величины называется законом равной вероятности, а само распределение — равномерным.

|
|
|
Рис. 6. График дифференциальной функции равномерного распределения |
|
Рис. 7. График интегральной функции равномерного распределения |
т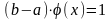
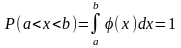 .
е. вероятность того, что случайная
величина х при испытаниях будет принимать
значения в интервале от
a
до
b,
равна площади под дифференциальной
кривой распределения. В соответствии
с рис. 6 эта площадь представляет собой
прямоугольник с основанием
ab
и высотой φ(x),
следовательно,
.
е. вероятность того, что случайная
величина х при испытаниях будет принимать
значения в интервале от
a
до
b,
равна площади под дифференциальной
кривой распределения. В соответствии
с рис. 6 эта площадь представляет собой
прямоугольник с основанием
ab
и высотой φ(x),
следовательно,
О тсюда
уравнение дифференциальной функции
распределения или плотности вероятности
будет иметь следующий вид:
тсюда
уравнение дифференциальной функции
распределения или плотности вероятности
будет иметь следующий вид:
З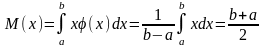 акон
равной вероятности имеет два параметра:
M(x)
и σ2,
которые согласно формулам и темы 1
равны откуда
акон
равной вероятности имеет два параметра:
M(x)
и σ2,
которые согласно формулам и темы 1
равны откуда
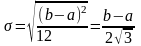
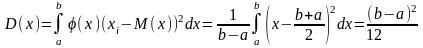
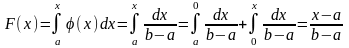
Интегральная функция равномерного распределения выражается следующим уравнением для (a < x < b):
Е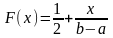 сли
x
< a,
то
F(x)
= 0; если x
≥
b,
то
F(x)
=
1. Когда a
= -b,
сли
x
< a,
то
F(x)
= 0; если x
≥
b,
то
F(x)
=
1. Когда a
= -b,
M(x) = 0,
то
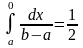 и для этого случая уравнение примет
вид
и для этого случая уравнение примет
вид
График интегральной функции распределения приведен на рис. 7. Законом равной вероятности описывается распределение показателей точности обработки, на величину которых оказывает влияние доминирующий фактор, изменяющийся во времени (износ инструмента, изменение температуры и т. п.).
З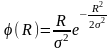 акон
распределения эксцентриситета, или
закон Релея,
имеет место при отклонениях эксцентриситета
осей или биении поверхностей деталей,
которые являются непрерывными случайными
величинами. Этот закон однопараметрический
и дифференциальная функция распределения
его имеет выражение: где R
— переменная величина эксцентриситета
или биения,
акон
распределения эксцентриситета, или
закон Релея,
имеет место при отклонениях эксцентриситета
осей или биении поверхностей деталей,
которые являются непрерывными случайными
величинами. Этот закон однопараметрический
и дифференциальная функция распределения
его имеет выражение: где R
— переменная величина эксцентриситета
или биения,
п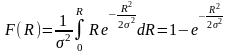 ричем
ричем
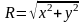 ,
а x
и
y
— координаты точки конца
R
(рис.
8); σ
- среднее квадратическое отклонение
значений координат x
и
y,
имеющих одинаковое распределение;
поэтому σ =
σx
= σy.
,
а x
и
y
— координаты точки конца
R
(рис.
8); σ
- среднее квадратическое отклонение
значений координат x
и
y,
имеющих одинаковое распределение;
поэтому σ =
σx
= σy.
Интегральный закон распределения эксцентриситета имеет выражение:
Графическое изображение дифференциального закона распределения эксцентриситета дано на рис. 9.
Особенностью данного распределения является то, что в основе его лежит нормальное распределение, так как координаты x и y точки конца R распределены нормально, но само
распределение
R
не является нормальным. Связь между
σR,
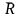 и σ
выражается следующими зависимостями:
и σ
выражается следующими зависимостями:
г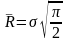
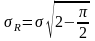 де
–среднее
значение (математическое ожидание)
случайной величины R;
де
–среднее
значение (математическое ожидание)
случайной величины R;
σR - среднее квадратическое отклонение R от .
З
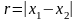 акон
модуля разности распределения случайных
величин. Уравнения и параметры этого
закона распределения. Случайные величины
процессов механической обработки и
качества деталей, распределение которых
может быть описано законом модуля
разности.
акон
модуля разности распределения случайных
величин. Уравнения и параметры этого
закона распределения. Случайные величины
процессов механической обработки и
качества деталей, распределение которых
может быть описано законом модуля
разности.
Если
две случайные величины x1
и
x2
каждая в отдельности имеют нормальное
распределение с параметрами
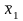 и
и
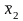 и
и
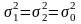 ,
то модуль разности этих величин
,
то модуль разности этих величин
и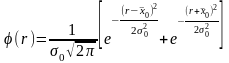 меет
распределение, которое носит название
закона
распределения модуля разности.
Этому закону распределения, например,
часто подчиняются погрешности взаимно
расположенных поверхностей и осей, а
также погрешности формы деталей:
овальность, конусность. Плотность
вероятности (дифференциальная функция)
распределения случайной величины
r
выражается следующим уравнением: где
меет
распределение, которое носит название
закона
распределения модуля разности.
Этому закону распределения, например,
часто подчиняются погрешности взаимно
расположенных поверхностей и осей, а
также погрешности формы деталей:
овальность, конусность. Плотность
вероятности (дифференциальная функция)
распределения случайной величины
r
выражается следующим уравнением: где
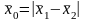 и σ0
являются параметрами распределения
модуля разности r.
и σ0
являются параметрами распределения
модуля разности r.
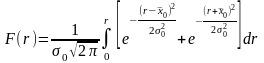
Интегральная функция распределения модуля разности r выражается следующим уравнением:
П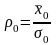

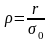 роизведя
замену переменных в уравнениях:
роизведя
замену переменных в уравнениях:
получим следующие выражения:

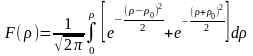
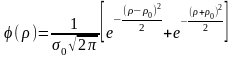
В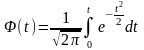
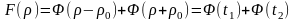 ид
кривой распределения φ(ρ) зависит от
значения ρ0.
При ρ0
= 0 кривая резко асимметрична, при ρ0
= 3 она совпадает с кривой нормального
распределения (рис. 10). Если обозначить
ρ - ρ0
= t1
ρ + ρ0
= t2
то уравнение (25) можно заменить следующим
уравнением:
ид
кривой распределения φ(ρ) зависит от
значения ρ0.
При ρ0
= 0 кривая резко асимметрична, при ρ0
= 3 она совпадает с кривой нормального
распределения (рис. 10). Если обозначить
ρ - ρ0
= t1
ρ + ρ0
= t2
то уравнение (25) можно заменить следующим
уравнением:
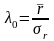 ,
так как каждое слагаемое уравнения
является функцией Лапласа:
,
так как каждое слагаемое уравнения
является функцией Лапласа:
Между
σr,
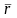 и ρ0
существует определенная зависимость,
которая определяется через нормированное
,
обозначаемое λ0:
и ρ0
существует определенная зависимость,
которая определяется через нормированное
,
обозначаемое λ0:
С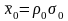
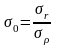 реднее
значение
и среднее квадратическое отклонение
σr
случайной
величины
r
вычисляются по экспериментальным
данным. По полученному значению λ0
определяют ρ0
при помощи табл. П.2 приложения, а по ρ0
определяют σρ
по табл. П.3 приложения.
реднее
значение
и среднее квадратическое отклонение
σr
случайной
величины
r
вычисляются по экспериментальным
данным. По полученному значению λ0
определяют ρ0
при помощи табл. П.2 приложения, а по ρ0
определяют σρ
по табл. П.3 приложения.
3ная
ρ0
и σρ,
можно определить параметры распределения
σ0
и
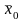 по следующим формулам:
по следующим формулам:
Пользуясь формулой (26) и известными из опыта значениями и σr можно вычислить вероятность того, что случайная величина r будет находиться в пределах заданных значений.
Экспоненциальный закон распределения случайных величин. Уравнения и параметры этого закона распределения. Случайные величины процессов механической обработки и качества деталей, распределение которых может быть описано экспоненциальным законом.
Э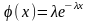 то
распределение относится к процессам,
в которых отказ элемента наступает
внезапно, т. е. независимо от того, сколько
времени он до этого находился в
эксплуатации и каково его состояние.
Этим законом описываются периоды времени
автоматического хода станков или
агрегатов автоматических линий, время
между простоями станков, длительность
регулировок и подналадок находящихся
в эксплуатации станков, приборов и
аппаратов, периоды безотказной работы
объектов и т. п. Плотность вероятности
случайной величины, распределение
которой подчиняется экспоненциальному
закону, определяется уравнением
то
распределение относится к процессам,
в которых отказ элемента наступает
внезапно, т. е. независимо от того, сколько
времени он до этого находился в
эксплуатации и каково его состояние.
Этим законом описываются периоды времени
автоматического хода станков или
агрегатов автоматических линий, время
между простоями станков, длительность
регулировок и подналадок находящихся
в эксплуатации станков, приборов и
аппаратов, периоды безотказной работы
объектов и т. п. Плотность вероятности
случайной величины, распределение
которой подчиняется экспоненциальному
закону, определяется уравнением
г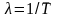 де
λ – постоянная (параметр закона
распределения) отражающая интенсивность
отказов (количество отказов в единицу
времени). Применительно к инструменту
параметр λ обычно определяется временем
де
λ – постоянная (параметр закона
распределения) отражающая интенсивность
отказов (количество отказов в единицу
времени). Применительно к инструменту
параметр λ обычно определяется временем
 наработки на отказ
наработки на отказ
И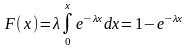 нтегральная
функция распределения описывается
формулой:
нтегральная
функция распределения описывается
формулой:
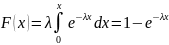
Закон распределения Вейбулла случайных величин. Уравнения и параметры этого закона распределения. Случайные величины процессов механической обработки и качества деталей, распределение которых может быть описано законом распределения Вейбулла.
Закон Вейбулла используется для описания распределения случайных величин, характеризующих прочность и долговечность различных устройств и их элементов (режущего инструмента, элементов радиоэлектронной аппаратуры и т. п.). Плотность вероятности распределения случайной величины, например стойкости инструмента T, по закону Вейбулла равна
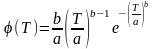
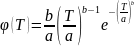
где a и b – параметры масштаба и формы кривой распределения.
Интегральная функция распределения вычисляется по формуле
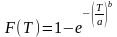
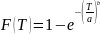
Закон логарифмического нормального распределения случайных величин. Уравнения и параметры этого закона распределения. Случайные величины процессов механической обработки и качества деталей, распределение которых может быть описано законом логарифмического нормального распределения.
Логарифмическое нормальное (логнормальное) распределение имеют характеристики усталостных испытаний материалов и устройств, износостойкости инструмента и др.
Логнормальное распределение – это распределение случайной величины x, распределение логарифма значений которой (t = lnx) подчиняется нормальному закону. Дифференциальная функция распределения случайной величины x описывается следующим уравнением:
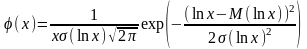

где
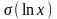
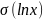 – среднее квадратическое отклонение
логарифма случайной величины x;
– среднее квадратическое отклонение
логарифма случайной величины x;
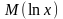
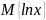 - математическое ожидание логарифма
случайной величины x.
- математическое ожидание логарифма
случайной величины x.
Интегральная функция распределения вычисляется по формуле
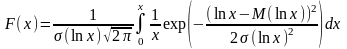
Основные понятия и определения теории выборок (генеральная совокупность, статистическая и эмпирическая совокупности). Выборка, виды выборок (повторная, бесповторная, мгновенная и общая выборки, большая и малая выборки).
Группа предметов, объединенных каким-либо общим признаком или свойством качественного или количественного характера, носит название статистической совокупности. Например, партия деталей представляет собой статистическую совокупность. Признак, по которому детали объединяются в совокупность, может быть количественным (размер) или качественным («брак», «не брак»). Следовательно, одни и те же предметы могут образовывать несколько совокупностей в зависимости от того, по какому признаку они объединяются в совокупность: количественному или качественному. Предметы, образующие совокупность, называются ее членами. Общее число членов совокупности составляет ее объем. Если совокупность содержит конечное число членов, полученных в результате испытаний, то она называется эмпирической. Эмпирическая совокупность может состоять из очень большого числа членов, изучение или обследование которых представляет весьма трудоемкую задачу. В математической статистике для обследования большой совокупности прибегают к выборкам из нее. Совокупность, из которой извлекается выборка, называется генеральной совокупностью. Выборкой называется часть членов совокупности, отобранных из нее для получения сведений о всей совокупности. Число членов, образующих выборку, составляет ее объем. Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо, чтобы члены выборки правильно его представляли. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной).
Виды выборок. По способу образования выборки делятся на повторные и бесповторные. Повторная выборка образуется путем последовательного извлечения из генеральной совокупности нескольких членов с возвратом каждого из них после соответствующего обследования обратно в генеральную совокупность. При извлечении следующего объекта из совокупности не исключена возможность снова вынуть этот же объект. Если из генеральной совокупности произведено n таких извлечений объекта, то говорят, что образована повторная выборка объема n. Например, из партии в 1000 шт. деталей последовательно извлекается 10 деталей в следующем порядке: извлекается первая деталь и измеряется, затем она возвращается в совокупность, последняя перемешивается, затем извлекается вторая деталь, производится ее измерение, снова деталь возвращается в совокупность, последняя перемешивается, извлекается следующая деталь и т. д. Извлеченные таким способом 10 деталей составят повторную выборку объемом в 10 шт. Бесповторная выборка образуется путем извлечения некоторого числа членов генеральной совокупности для необходимого обследования без возврата этих членов в совокупность. Например, если из партии в 1000 шт. деталей сразу или последовательно будет извлечено 10 деталей без возвращения их обратно, то будет образована бесповторная выборка объемом в 10 шт. Выборка считается преднамеренной, если отбор объектов для нее из генеральной совокупности производится с определенной тенденцией, приводящей к повышению или понижению вероятности выявления изучаемого признака качества. Выборка считается случайной, если все объекты генеральной совокупности имеют равную возможность попасть в выборку. Для образования случайных выборок пользуются либо отбором по жребию, либо путем тщательного перемешивания предметов в ящике и отбора их наудачу из разных мест ящика. Мгновенной (или текущей) выборкой называется выборка малого объема, взятая из числа единиц потока продукции, изготовленных к моменту отбора в короткий промежуток времени, в котором проявление систематических погрешностей пренебрежимо мало. Общей выборкой называется выборка, состоящая из серии мгновенных выборок. Малой выборкой считается выборка, объем которой меньше 25 членов. Если объем выборки больше 25 членов, то она считается большой. В производственных исследованиях обычно большая выборка состоит из 50-100 или более членов, а малая выборка из 5-10 членов.
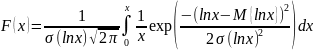
Оценки параметров генеральной совокупности (выборочные средние и дисперсии). Понятия состоятельности, несмещенности и эффективности оценок параметров генеральной совокупности. Свойства выборочной средней и выборочной дисперсии.
Б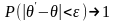 еря
выборку из генеральной совокупности и
вычисляя ее статистические характеристики
и
s,
можно с некоторым приближением считать,
что они по своим величинам будут близки
к соответствующим параметрам генеральной
совокупности
и σ0,
т. е. являться их
оценками.
Но для того чтобы эти оценки достаточно
правильно и близко характеризовали
параметры генеральной совокупности,
необходимо, чтобы они удовлетворяли
трем требованиям: были бы состоятельными,
несмещенными и эффективными.
Оценка называется
состоятельной,
если вероятность отклонения ее от
оцениваемого параметра на величину,
меньшую как угодно малого положительного
числа ε, стремится к единице при
неограниченном увеличении числа
п
наблюдений, т. е. при ε > 0 и n→
∞, где θ — некоторый параметр генеральной
совокупности;
θ'
— оценка этого параметра.
еря
выборку из генеральной совокупности и
вычисляя ее статистические характеристики
и
s,
можно с некоторым приближением считать,
что они по своим величинам будут близки
к соответствующим параметрам генеральной
совокупности
и σ0,
т. е. являться их
оценками.
Но для того чтобы эти оценки достаточно
правильно и близко характеризовали
параметры генеральной совокупности,
необходимо, чтобы они удовлетворяли
трем требованиям: были бы состоятельными,
несмещенными и эффективными.
Оценка называется
состоятельной,
если вероятность отклонения ее от
оцениваемого параметра на величину,
меньшую как угодно малого положительного
числа ε, стремится к единице при
неограниченном увеличении числа
п
наблюдений, т. е. при ε > 0 и n→
∞, где θ — некоторый параметр генеральной
совокупности;
θ'
— оценка этого параметра.
О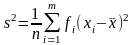 ценка
называется
несмещенной,
т. е. в ней отсутствуют систематические
погрешности, если математическое
ожидание этой оценки равно оцениваемому
параметру М(θ')
= θ.
Если
М(θ')
> 0, то оценку называют
положительно
смещенной;
если
М(θ') < 0,
то
отрицательно
смещенной.
Примером
состоятельной и несмещенной оценки
математического ожидания является
средняя арифметическая. Примером
состоятельной, но смещенной оценки
теоретической дисперсии σ2
может
служить эмпирическая дисперсия s2
где
fi
- частота значений xi;
n
- общее число наблюденных значений xi,
;
m
- число отдельных значений
xi.
ценка
называется
несмещенной,
т. е. в ней отсутствуют систематические
погрешности, если математическое
ожидание этой оценки равно оцениваемому
параметру М(θ')
= θ.
Если
М(θ')
> 0, то оценку называют
положительно
смещенной;
если
М(θ') < 0,
то
отрицательно
смещенной.
Примером
состоятельной и несмещенной оценки
математического ожидания является
средняя арифметическая. Примером
состоятельной, но смещенной оценки
теоретической дисперсии σ2
может
служить эмпирическая дисперсия s2
где
fi
- частота значений xi;
n
- общее число наблюденных значений xi,
;
m
- число отдельных значений
xi.
Д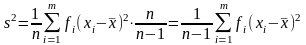 ля
непрерывных случайных величин в качестве
xi
принимают середину интервалов, на
которые разбивается наблюденный ряд
значений x.
Из
выражения для оценки s2
следует, что с увеличением
n
вероятность
Р(|
s2
- σ2
| < ε) → 1 и, следовательно, s2
является состоятельной оценкой, но
математическое ожидание
ля
непрерывных случайных величин в качестве
xi
принимают середину интервалов, на
которые разбивается наблюденный ряд
значений x.
Из
выражения для оценки s2
следует, что с увеличением
n
вероятность
Р(|
s2
- σ2
| < ε) → 1 и, следовательно, s2
является состоятельной оценкой, но
математическое ожидание
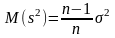 не равно σ2
и при конечном
n
дает уменьшенное значение оцениваемого
параметра σ2,
поэтому, оценивая σ2
по s2,
мы допускаем систематическую ошибку,
равную
не равно σ2
и при конечном
n
дает уменьшенное значение оцениваемого
параметра σ2,
поэтому, оценивая σ2
по s2,
мы допускаем систематическую ошибку,
равную
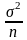 ,
однако при больших
n
она пренебрежимо мала. Для того чтобы
получить несмещенную оценку теоретической
дисперсии σ2
по эмпирическим данным, необходимо
эмпирическую дисперсию s2
умножить на
,
однако при больших
n
она пренебрежимо мала. Для того чтобы
получить несмещенную оценку теоретической
дисперсии σ2
по эмпирическим данным, необходимо
эмпирическую дисперсию s2
умножить на
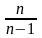 ,
т. е.
,
т. е.
Практически эту поправку вносят при вычислении оценки дисперсии в тех случаях, когда n < 30.
Состоятельных несмещенных оценок может быть несколько. Например, для оценки центра рассеивания нормального распределения, наряду со средней арифметической , может быть взята медиана Ме. Медиана так же, как и , является несмещенной состоятельной оценкой центра группирования. Из двух состоятельных несмещенных оценок θ' и θ" для одного и того же параметра θ естественно отдать предпочтение той, у которой дисперсия меньше. Такая оценка, у которой дисперсия будет наименьшей относительно θ, называется эффективной. Например, из двух оценок центра рассеивания нормального распределения эффективной оценкой является , а не Ме, так как дисперсия меньше дисперсии Ме. Сравнительная эффективность Ме при большой выборке приближенно равна.
П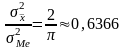 рактически
это означает, что центр распределения
генеральной совокупности
определяется
по медиане Ме
с той
же точностью при п
наблюдениях,
как при 0,6366 п
наблюдениях
по средней арифметической
.
При решении задач, осуществляемых
посредством выборочного метода, важное
значение приобретают свойства выборочной
средней и выборочной дисперсии, которые
приведены ниже без доказательств.
рактически
это означает, что центр распределения
генеральной совокупности
определяется
по медиане Ме
с той
же точностью при п
наблюдениях,
как при 0,6366 п
наблюдениях
по средней арифметической
.
При решении задач, осуществляемых
посредством выборочного метода, важное
значение приобретают свойства выборочной
средней и выборочной дисперсии, которые
приведены ниже без доказательств.
С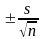 войства
выборочных средних и дисперсий.. 1
Если объем выборки достаточно велик,
то на основе закона больших чисел с
вероятностью, как угодно близкой к
достоверности, можно утверждать, что
средняя арифметическая
и дисперсия s2
выборки будут как угодно мало отличаться
от генеральной средней
и генеральной дисперсии
войства
выборочных средних и дисперсий.. 1
Если объем выборки достаточно велик,
то на основе закона больших чисел с
вероятностью, как угодно близкой к
достоверности, можно утверждать, что
средняя арифметическая
и дисперсия s2
выборки будут как угодно мало отличаться
от генеральной средней
и генеральной дисперсии
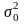 ,
т. е.
,
т. е.
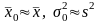 ,
если
,
если
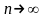 ,
где п
—
объем выборки.
2
Ошибка вычисления генеральной средней
по средней
выборки
зависит от ее объема п
и
равна .
,
где п
—
объем выборки.
2
Ошибка вычисления генеральной средней
по средней
выборки
зависит от ее объема п
и
равна .
О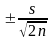 шибка
вычисления среднего квадратического
отклонения генеральной совокупности
по среднему квадратическому отклонению
выборки зависит от ее объема и равна .
шибка
вычисления среднего квадратического
отклонения генеральной совокупности
по среднему квадратическому отклонению
выборки зависит от ее объема и равна .
3
Если случайная величина х
в
генеральной совокупности имеет нормальное
распределение со средней
и
дисперсией
,
то и средние арифметические
выборок
из этой совокупности будут подчинены
также нормальному распределению со
средней
 и дисперсией
и дисперсией
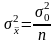 ,
каков бы ни был объем выборок п,
лишь
бы число выборок было достаточно велико.
4
Когда дисперсия
генеральной совокупности не известна,
тогда для больших значений п
с
большей вероятностью малой ошибки можно
дисперсию выборочных средних вычислять
приближенно по равенству
,
каков бы ни был объем выборок п,
лишь
бы число выборок было достаточно велико.
4
Когда дисперсия
генеральной совокупности не известна,
тогда для больших значений п
с
большей вероятностью малой ошибки можно
дисперсию выборочных средних вычислять
приближенно по равенству
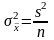 где
s2
— дисперсия большой выборки объема n,
вычисляемая по формуле:
где
s2
— дисперсия большой выборки объема n,
вычисляемая по формуле:
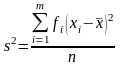 .
5
Приведенная выше связь дисперсии
выборочных средних с дисперсией
генеральной совокупности
в виде соотношения
.
5
Приведенная выше связь дисперсии
выборочных средних с дисперсией
генеральной совокупности
в виде соотношения
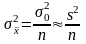 действительна для повторных выборок.
Для бесповторных выборок эта связь
выражается зависимостью
действительна для повторных выборок.
Для бесповторных выборок эта связь
выражается зависимостью
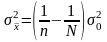 ,
где п
—
объем выборки;
N
— объем генеральной совокупности. Если
N
по
сравнению с n
очень велико, что практически всегда
имеет место, то для бесповторных выборок
можно пользоваться для вычисления
,
где п
—
объем выборки;
N
— объем генеральной совокупности. Если
N
по
сравнению с n
очень велико, что практически всегда
имеет место, то для бесповторных выборок
можно пользоваться для вычисления
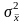 формулой, при этом ошибка будет весьма
ничтожной.
формулой, при этом ошибка будет весьма
ничтожной.
Из
свойств выборочных средних и дисперсий
следует, что точность вычислений средних
арифметических и дисперсий или средних
квадратических отклонений генеральной
совокупности по данным выборки из нее
зависит от объема выборки, причем
точность возрастает с ростом объема
выборки. Однако практически не всегда
бывает возможным или легко осуществимым
взятие больших выборок или проведение
большого числа наблюдений. Часто на
практике приходится ограничиваться
взятием небольших выборок или
ограничиваться малым числом наблюдений.
В этих случаях важно сделать оценку
точности и надежности приближенных
равенств
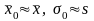 ,
где
— среднее арифметическое значение
случайной величины
генеральной
совокупности;
— то же в выборке объема п
из
генеральной совокупности; σ0
— среднее квадратическое отклонение
генеральной совокупности; s
— среднее квадратическое отклонение
выборки.
,
где
— среднее арифметическое значение
случайной величины
генеральной
совокупности;
— то же в выборке объема п
из
генеральной совокупности; σ0
— среднее квадратическое отклонение
генеральной совокупности; s
— среднее квадратическое отклонение
выборки.
Оценка точности вычисления генеральной средней по данным выборки. Пояснить методику оценки точности вычисления генеральной средней по данным выборки на следующей задаче: «По выборке объема n = 20 найдено = 15,8 и s = 0,55. Определить точность ε приближенного равенства
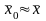 при вероятности α = 0,95».
при вероятности α = 0,95».
Обозначим
точность приближенного равенства
буквой ε. Тогда определение точности
вычисления генеральной средней по
данным выборки сведется к определению
вероятности α того, что истинное значение
находится в пределах
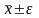 ,
где ε > 0, т. е.
,
где ε > 0, т. е.
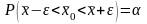 .
.
Для
определения вероятности а пользуются
распределением величины t:
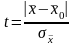 .
Если генеральная совокупность имеет
нормальное распределение, то величина
t
при
любом п
следует
закону распределения Стьюдента, который
имеет следующее выражение:
.
Если генеральная совокупность имеет
нормальное распределение, то величина
t
при
любом п
следует
закону распределения Стьюдента, который
имеет следующее выражение:
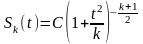 ,
где Sk(t)
— дифференциальная функция распределения
t;
,
где Sk(t)
— дифференциальная функция распределения
t;
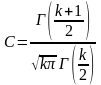 — постоянный
множитель, зависящий только от числа
степеней свободы k
= п -
1. Символом Г(k)
здесь
обозначена гамма-функция (интеграл
Эйлера):
— постоянный
множитель, зависящий только от числа
степеней свободы k
= п -
1. Символом Г(k)
здесь
обозначена гамма-функция (интеграл
Эйлера):
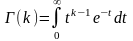 .
Из
выражения следует, что распределение
Стьюдента зависит только от переменной
t
и
параметра k
= п
-
1. Поэтому когда задана вероятность α,
то можно найти такое положительное
число tα
которое
будет зависеть только от α и n
по равенству
.
Из
выражения следует, что распределение
Стьюдента зависит только от переменной
t
и
параметра k
= п
-
1. Поэтому когда задана вероятность α,
то можно найти такое положительное
число tα
которое
будет зависеть только от α и n
по равенству
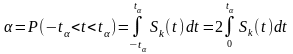 . Учитывая,
что
,
левую часть этого равенства можно
преобразовать так:
. Учитывая,
что
,
левую часть этого равенства можно
преобразовать так:
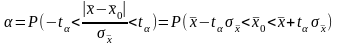 .
Следовательно,
.
Следовательно,
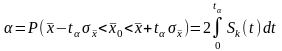 .
Полагая
.
Полагая
 ,
получим
,
получим
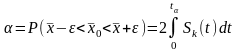 .
Таблица
значений tα
определяемых этим равенством, приведена
в табл. П.1 приложения (см. в конце темы).
При помощи этой таблицы можно определить
одно из трех значений: вероятность α,
точность ε или объем выборки п,
задаваясь
предварительно значениями каких-либо
двух из этих величин.
.
Таблица
значений tα
определяемых этим равенством, приведена
в табл. П.1 приложения (см. в конце темы).
При помощи этой таблицы можно определить
одно из трех значений: вероятность α,
точность ε или объем выборки п,
задаваясь
предварительно значениями каких-либо
двух из этих величин.
Оценка точности вычисления среднего квадратического отклонения генеральной совокупности по данным выборки. Пояснить методику оценки точности вычисления по данным выборки среднего квадратического отклонения на следующей задаче: «Определить точность ε приближенного равенства
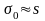 с вероятностью α = 0,95, если п
= 20
и s
= 0,17».
с вероятностью α = 0,95, если п
= 20
и s
= 0,17».
На
практике иногда необходимо найти
неизвестное среднее квадратическое
отклонение генеральной совокупности
σ0
по среднему квадратическому отклонению
s
малой выборки, когда ее объем n
< 30. Для малых выборок s
вычисляется по формуле
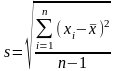 ,
где
в знаменателе берется (п - 1),
для того чтобы компенсировать
систематическую ошибку, возникающую
при оценке σ0
по s
при малом числе n.
Эта
задача сводится к определению вероятности
α приближенного равенства
,
точность которого равна ε:
,
где
в знаменателе берется (п - 1),
для того чтобы компенсировать
систематическую ошибку, возникающую
при оценке σ0
по s
при малом числе n.
Эта
задача сводится к определению вероятности
α приближенного равенства
,
точность которого равна ε:
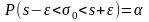 .
Если известно, что случайная величина
х
в
генеральной совокупности подчинена
нормальному закону распределения, то
величина
.
Если известно, что случайная величина
х
в
генеральной совокупности подчинена
нормальному закону распределения, то
величина
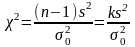 имеет
распределение, которое носит название
имеет
распределение, которое носит название
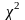 -распределения.
Дифференциальная функция этого
распределения (плотность вероятности)
величины
имеет выражение
-распределения.
Дифференциальная функция этого
распределения (плотность вероятности)
величины
имеет выражение
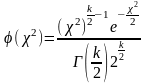 при
χ > 0. При помощи этой функции
-распределения
можно вычислить и вероятность α:
при
χ > 0. При помощи этой функции
-распределения
можно вычислить и вероятность α:
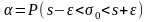 .
Для
этой цели, полагая, что s
- ε > 0, преобразуем находящееся в скобках
неравенство следующим образом:
.
Для
этой цели, полагая, что s
- ε > 0, преобразуем находящееся в скобках
неравенство следующим образом:
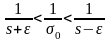 .
Умножим
полученное неравенство на положительное
число
.
Умножим
полученное неравенство на положительное
число
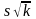
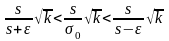 .
Обозначив
.
Обозначив
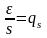 и
и
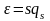 ,
получим
,
получим
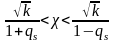 или
или
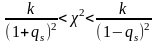 .
Вероятность
этого неравенства равна интегралу
.
Вероятность
этого неравенства равна интегралу
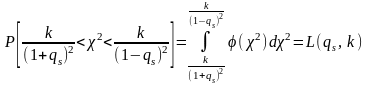 .
Но
левая часть этого уравнения есть
преобразованное выражение вероятности
.
Следовательно,
можно написать
.
Но
левая часть этого уравнения есть
преобразованное выражение вероятности
.
Следовательно,
можно написать
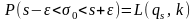 или
или
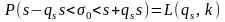 .
Значения
интеграла L(qs,
k)
приведены
в табл. П.2 приложения.
Таким
образом, по табл. П.2 приложения можно
определить вероятность α, т. е. вероятность
того, что отклонения σ0
от s
не превосходят ε = qss.
Необходимо
заметить, что если s
< ε, то исходное неравенство для σ0
.
Значения
интеграла L(qs,
k)
приведены
в табл. П.2 приложения.
Таким
образом, по табл. П.2 приложения можно
определить вероятность α, т. е. вероятность
того, что отклонения σ0
от s
не превосходят ε = qss.
Необходимо
заметить, что если s
< ε, то исходное неравенство для σ0
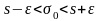 надо
заменить неравенством
надо
заменить неравенством
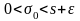 ,
так
как величина σ0
должна быть положительной. В этом случае
неравенство для χ
примет вид
,
так
как величина σ0
должна быть положительной. В этом случае
неравенство для χ
примет вид
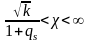 и
вероятность его будет определяться
интегралом
и
вероятность его будет определяться
интегралом
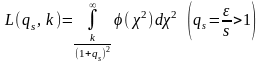 .
Значения
этого интеграла также приведены в табл.
П.2 приложения. При помощи этой таблицы
значений вероятностей L(qs,
k)
можно решать задачи трех типов:
1)
по заданной точности ε = qss
и объеме выборки n
определить вероятность α приближенного
равенства
;
2)
по заданной вероятности α приближенного
равенства
и объеме выборки п
определить
точность ε = qss
этого равенства;
3)
по заданной точности ε и вероятности α
приближенного равенства
определить необходимый объем n
выборки.
.
Значения
этого интеграла также приведены в табл.
П.2 приложения. При помощи этой таблицы
значений вероятностей L(qs,
k)
можно решать задачи трех типов:
1)
по заданной точности ε = qss
и объеме выборки n
определить вероятность α приближенного
равенства
;
2)
по заданной вероятности α приближенного
равенства
и объеме выборки п
определить
точность ε = qss
этого равенства;
3)
по заданной точности ε и вероятности α
приближенного равенства
определить необходимый объем n
выборки.
Статистическая гипотеза. Основные понятия: параметрические и непараметрические гипотезы, критерии значимости и согласия, уровень значимости критерия. Последовательность проверки статистической гипотезы.
Статистическая гипотеза – это содержательное высказывание о свойствах генеральной совокупности, исходя из свойств выборки x1, x2,…, xn из этой генеральной совокупности.
Статистические гипотезы делятся на: параметрические – гипотезы, сформулированные относительно параметров распределения известного вида (среднего арифметического значения, дисперсии и т. п.); непараметрические - гипотезы, сформулированные относительно вида распределения, например, предположение по распределению данных выборки о нормальном законе генеральной совокупности. В математической статистике процесс проверки гипотезы включает в себя постановку и определение достоверности основной, так называемой «нулевой гипотезы» H0. Постановка «нулевой гипотезой» заключается в формулировке допущения об отсутствии интересующего нас различия между выборкой и ее генеральной совокупностью. Например, нас интересует, можно ли по полученному распределению в большой выборке из генеральной совокупности считать, что последняя имеет нормальное распределение. Для того чтобы прийти к вполне определенному заключению, хотя бы и вероятностного характера, мы делаем гипотетическое допущение, что распределение выборки несущественно отличается от нормального и, следовательно, на основании закона больших чисел можно считать, что и генеральная совокупность имеет нормальное распределение. Другими словами, мы выдвигаем «нулевую гипотезу» H0: данная выборка взята из нормальной совокупности. Наряду с нулевой гипотезой H0 рассматривается альтернативная ей гипотеза H1. Для выше приведенной нулевой гипотезы H0 альтернативная ей гипотеза может быть сформулирована как H1: данная выборка не принадлежит нормальной совокупности. Далее осуществляется проверка этих гипотез. Проверка нуль – гипотезы производится с использованием различных статистических критериев, позволяющих с помощью их уровней значимости q сделать вывод об опровержении гипотезы H0 и принятии альтернативной ей гипотезы H1. Статистическим критерием K называют случайную величину, с помощью которой принимают решение о принятии или отклонении нуль - гипотезы H0. Различают критерии значимости и критерии согласия. Критерии значимости используются для проверки гипотез о параметрах распределения генеральной совокупности (проверки параметрических гипотез). К ним относятся критерии Стьюдента, Фишера и др. Критерии согласия применяют для проверки гипотез о законах статистических распределений. Из этих критериев широко используются критерий λ А.Н. Колмогорова и критерий К. Пирсона. Уровень значимости q критерия K представляет собой достаточно малое значение вероятности, отвечающее событиям, которые в данной обстановке исследования можно считать практически невозможными. Обычно принимают пяти- двух- или однопроцентный уровень значимости. В технике чаще всего принимают пятипроцентный уровень значимости. Эти уровни значимости соответствуют классификации явлений на редкие (q = 0,05), очень редкие (q = 0,01) и чрезвычайно редкие (q = 0,001). Выбирая тот или иной уровень значимости q критерия K, мы тем самым устанавливаем и область допустимых его значений, при которых выдвинутая гипотеза считается достоверной.
Последовательность проверки гипотез включает следующие операции:
формулируется «нулевая гипотеза»;
выбирается уровень значимости;
выбирается критерий согласия и определяется его критическое значение (по соответствующей таблице математической статистики);
вычисляется по результатам выборки расчетное (выборочное) значение критерия согласия;
принимается или отвергается нуль-гипотеза.
Выравнивание статистических рядов. Понятие простой статистической совокупности (простого статистического ряда) и статистического ряда. Два подхода в определении закона распределения случайной величины при визуальном анализе ее полигона распределения. Методика выравнивания статистического распределения случайной величины.
Изучается некоторая случайная величина X, закон распределения которой в точности не известен. Требуется определить этот закон из опыта или проверить экспериментально гипотезу о том, что величина X подчинена тому или иному закону. С этой целью над случайной величиной производится ряд независимых опытов (наблюдений). В каждом из этих опытов случайная величина X принимает определенное значение. Совокупность наблюденных значений величины X представляет первичный статистический материал, подлежащий обработке, осмыслению и научному анализу. Такую совокупность принято называть простой статистической совокупностью или простым статистическим рядом.
Для
определения закона распределения
случайной величины существуют два
подхода.
Первый
подход
основан на подборе, исходя из внешнего
вида статистического распределения,
наиболее подходящей функции для его
аналитического описания. В принципе
выравнивание статистического ряда
можно осуществить с помощью любой
аналитической функции, обладающей
основными свойствами плотности
распределения φ(x):
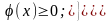 .
Такой
подход выбора закона распределения
обладает существенным недостатком, а
именно, выбранная функция в качестве
закона статистического распределения
не отражает физическую сущность
исследуемого объекта. Определение
закона статистического распределения
при
втором подходе
осуществляется путем выбора теоретической
кривой из существующих в теории
вероятностей и математической статистике
теоретических распределений. Основанием
такого подхода служит то, что разработанные
в теории вероятностей и математической
статистике теоретические законы
распределения имеют своим источником
реальные процессы и получены логическим
путем с использованием физических
характеристик этих процессов. Это
позволяет выполнить выбор вида
теоретической кривой не по внешним
формальным признакам, а по близости
(общности) физической сущности
рассматриваемого случайного процесса
и выбираемого теоретического закона
распределения1.
В данном случае обеспечивается выбор
теоретического закона, аналитическое
выражение которого содержит параметры,
характеризующие физическую сущность
исследуемого случайного процесса или
явления. При этом задача выравнивания
статистического ряда переходит в задачу
рационального выбора таких значений
параметров закона распределения, при
которых соответствие между статистическим
и теоретическим распределением
оказывается наилучшим.
.
Такой
подход выбора закона распределения
обладает существенным недостатком, а
именно, выбранная функция в качестве
закона статистического распределения
не отражает физическую сущность
исследуемого объекта. Определение
закона статистического распределения
при
втором подходе
осуществляется путем выбора теоретической
кривой из существующих в теории
вероятностей и математической статистике
теоретических распределений. Основанием
такого подхода служит то, что разработанные
в теории вероятностей и математической
статистике теоретические законы
распределения имеют своим источником
реальные процессы и получены логическим
путем с использованием физических
характеристик этих процессов. Это
позволяет выполнить выбор вида
теоретической кривой не по внешним
формальным признакам, а по близости
(общности) физической сущности
рассматриваемого случайного процесса
и выбираемого теоретического закона
распределения1.
В данном случае обеспечивается выбор
теоретического закона, аналитическое
выражение которого содержит параметры,
характеризующие физическую сущность
исследуемого случайного процесса или
явления. При этом задача выравнивания
статистического ряда переходит в задачу
рационального выбора таких значений
параметров закона распределения, при
которых соответствие между статистическим
и теоретическим распределением
оказывается наилучшим.
Методика
выравнивания.
Так, исследуемая в примере 1 случайная
величина X
есть погрешность размера деталей,
обработанных на станке, настроенном на
заданный размер детали. Эта погрешность
обработки обусловлена действием
множества случайных независимых факторов
(вариации твердости материала заготовок
детали, колебанием размера заготовок
и т. д.). Из анализа результатов,
представленных в виде статистического
ряда (табл. 6) и теоретических соображений
можно считать, что распределение величины
X
подчиняется нормальному закону:
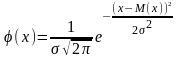 .
Таким образом, задача выравнивания
статистического ряда переходит в задачу
о рациональном выборе параметров M(x)
и σ в выражении. Обычно принимают, что
параметры выбранного теоретического
закона распределения равны соответствующим
статистическим параметрам. В частности,
для приведенного закона принимают, что
.
Таким образом, задача выравнивания
статистического ряда переходит в задачу
о рациональном выборе параметров M(x)
и σ в выражении. Обычно принимают, что
параметры выбранного теоретического
закона распределения равны соответствующим
статистическим параметрам. В частности,
для приведенного закона принимают, что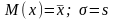 . Построив
с использованием условий теоретическую
кривую распределения и сопоставив ее
со статическим распределением,
представленным, например, в виде
гистограммы, можно визуально оценить
близость теоретического и статического
распределения (рис. 2). Вместе с тем, как
бы хорошо ни была подобрана теоретическая
кривая, между ней и статистическим
распределением неизбежны некоторые
расхождения. Поэтому возникает вопрос,
обусловлены ли эти расхождения только
случайными воздействиями и связаны с
ограниченным числом наблюдений, или
они являются существенными и вызваны
тем, что подобранная теоретическая
кривая плохо выравнивает исследуемое
статистическое распределение. Для
ответа на этот вопрос осуществляют
проверку гипотезы о законе распределения
с помощью критериев согласия.
. Построив
с использованием условий теоретическую
кривую распределения и сопоставив ее
со статическим распределением,
представленным, например, в виде
гистограммы, можно визуально оценить
близость теоретического и статического
распределения (рис. 2). Вместе с тем, как
бы хорошо ни была подобрана теоретическая
кривая, между ней и статистическим
распределением неизбежны некоторые
расхождения. Поэтому возникает вопрос,
обусловлены ли эти расхождения только
случайными воздействиями и связаны с
ограниченным числом наблюдений, или
они являются существенными и вызваны
тем, что подобранная теоретическая
кривая плохо выравнивает исследуемое
статистическое распределение. Для
ответа на этот вопрос осуществляют
проверку гипотезы о законе распределения
с помощью критериев согласия.
Критерии согласия λ и χ2, используемые при проверке гипотезы о законе распределения случайной величины. Методика определения значений λ и χ2 по данным статистического ряда распределения случайной величины.
Критерий λ. Этот критерий дает достаточно точные результаты даже при объеме выборок, состоящих из нескольких десятков членов и прост для вычислений.
Для
вычисления величины λ необходимо
предварительно определить значения
эмпирической Fэ(х)
и теоретической F(х)
интегральной функции предполагаемого
закона распределения для каждого
наблюденного значения случайной величины
х.
Затем по максимальной разности значений
этих функций определяется λ при помощи
следующей формулы:
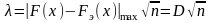 .
(4) Так как
.
(4) Так как
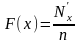 и
и
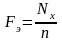 ,
где
,
где
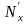 и
и
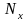 - накопленные теоретические и эмпирические
частоты, а n
— объем выборки, то вместо формулы (4)
можно пользоваться следующей формулой:
- накопленные теоретические и эмпирические
частоты, а n
— объем выборки, то вместо формулы (4)
можно пользоваться следующей формулой:
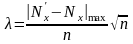 . (5) Накопленной частотой любого m-го
значения xi
называется сумма частот всех предшествующих
значений xi,
включая и частоту самого xi,
т. е.
. (5) Накопленной частотой любого m-го
значения xi
называется сумма частот всех предшествующих
значений xi,
включая и частоту самого xi,
т. е.
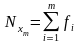 (6), где m
— число значений хi;
fi
- частота i-го
значения х.
Академик А. Н. Колмогоров доказал, что
для непрерывных случайных величин
(6), где m
— число значений хi;
fi
- частота i-го
значения х.
Академик А. Н. Колмогоров доказал, что
для непрерывных случайных величин
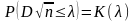 ,
где
,
где
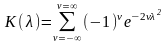 .
Для больших n
и любом
> 0
.
Для больших n
и любом
> 0
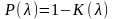 .
Функция K(λ)
табулирована Н. В. Смирновым и при помощи
таблицы значений K(λ)
составлена таблица значений P(λ),
которая приведена ниже (табл. 1).
.
Функция K(λ)
табулирована Н. В. Смирновым и при помощи
таблицы значений K(λ)
составлена таблица значений P(λ),
которая приведена ниже (табл. 1).
По вычисленному по формуле (4) или (5) значению λ по табл. 1 определяют P(λ). Если вероятность P(λ) окажется очень малой, практически, когда P(λ) ≤ 0,05, то расхождение между F(x) и Fэ(х) считается существенным, а не случайным и гипотеза о предполагаемом законе распределения величины x бракуется. Если же вероятность P(λ) будет достаточно большой (практически, когда P(λ) > 0,05), то гипотеза принимается.
Таблица 1
Значения вероятностей Р (λ) для различных λ
|
P() |
|
P() |
|
P() |
|
P() |
0,30 |
1,000 |
0,70 |
0,7112 |
1,20 |
0,1122 |
1,90 |
0,0015 |
0,35 |
0,9997 |
0,75 |
0,6272 |
1,30 |
0,0681 |
2,00 |
0,0007 |
0,40 |
0,9972 |
0,80 |
0,5441 |
1,40 |
0,0397 |
2,10 |
0,0003 |
0,45 |
0,9874 |
0,85 |
0,4653 |
1,50 |
0,0222 |
2,20 |
0,0001 |
0,50 |
0,9639 |
0,90 |
0,3927 |
1,60 |
0,0120 |
2,30 |
0,0001 |
0,55 |
0,9228 |
0,95 |
0,3275 |
1,70 |
0,0062 |
2,40 |
0,0000 |
0,60 |
0,8643 |
1,00 |
0,2700 |
1,80 |
0,0032 |
2,50 |
0,0000 |
0,65 |
0,7920 |
1,10 |
0,1777 |
|
|
|
|
Использование
критерия λ предполагает непрерывность
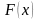 и, кроме того, предполагается, что
эмпирическая функция
и, кроме того, предполагается, что
эмпирическая функция
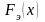 построена по не сгруппированным в
интервалы значениям случайной величины
х.
Однако в случае, когда интервалы
группировки достаточно малы, критерий
λ дает, хотя и приближенную, но вполне
приемлемую для практических целей
оценку близости эмпирического
распределения к теоретическому.
построена по не сгруппированным в
интервалы значениям случайной величины
х.
Однако в случае, когда интервалы
группировки достаточно малы, критерий
λ дает, хотя и приближенную, но вполне
приемлемую для практических целей
оценку близости эмпирического
распределения к теоретическому.
Для удобства вычисления критерия λ составляют вспомогательную таблицу, в которой накопленные частоты функции и вычисляются в зависимости от закона распределения х (табл. 2).
Таблица 2
