9.Механизмы трехзвенных зубчатых передач.
Это простейший механизм зубчатых передач.
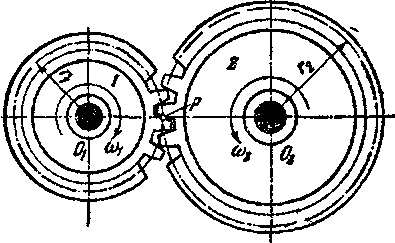
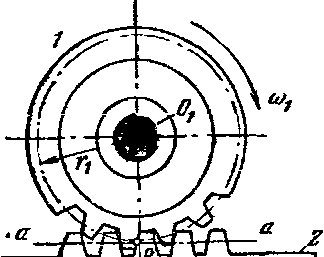
Если
известны радиусы начальных окружностей
колес, то можно найти передаточное
отношение
10.Регулирование скорости движения механизма.
Задача регулятора состоит в установлении устойчивого (стационарного) изменения скорости, режима движения начального звена регулируемого объекта, что может быть достигнуто выравниванием разницы между движущими силами и силами сопротивления. Если по каким-либо причинам уменьшается полезное сопротивление и регулируемый объект начинает ускорять свое движение, то регулятор автоматически уменьшает приток движущих сил. Наоборот, если силы сопротивления увеличиваются и регулируемый объект начинает замедлять свое движение, то регулятор увеличивает движущие силы. Таким образом, как только нарушается равновесие между движущими силами и силами сопротивления, регулятор должен вновь их сбалансировать и заставить регулируемый объект работать с прежними или близкими к прежним скоростями. Конструкции регуляторов и схемы регулирования разнообразны. Например, в практике применяются так называемые центробежные регуляторы, плоские и пространственные, в которых используется центробежная сила инерции. Имеются также инерционные регуляторы, использующие тангенциальные силы инерции. Применяются регуляторы электрического типа и др.
12.Механизмы плантарных зубчатых передач.
13.Структурная классификация плоских механизмов.
14.Как определяются моменты сил инерции?
15.Коэффициент неравномерности движения механизмов. Характеристика режимов работы механизмов.
16.Профилирование кулачка. Силовой расчет кулачкового механизма.
17.Определение скоростей и укреплений звеньев кинематических пар.
18.Приведение сил и масс в механизмах
19.Синтез кулачкового механизма при известном законе – ускорении ведомого звена.
20.Механический КПД.
21.Построение кинематических диаграмм. Кинематическое исследование механизмов методом диаграмм.
22. Сформулировать цель силового анализа. Сущность метода кинетостатики.
23.Перманентное начальное движение механизма. Определение положений звеньев группы и построение траекторий описываемых точками звеньев механизма.
А)Перманентное движение механизма т.е движение при котором угловая скорость кривошипа постоянна т.е =const.
Б)Начальное движение- скорости всех звеньев мех-ма равны нулю.Для изучения этого движения мех-ма надо построить только план ускорений в начальном движении.
В)Для определения положения звеньев механизма должны быть заданы кинематическая схема мех-ма,и функция перемещений ведущего звена для мех-ма с одной степенью подвижности или фунцкции перемещения ведущих звеньев для мех - ма с несколькими степенями подвижности .Кинематическая схема должна быть построена в масштабе, что бы можно было измерить ее линейкой . Для построения траектории движения звеньев надо знать функцию перемещения ведущего звена.
24.Уравнение движения механизма в энергетической форме
Уравнения движения механизма могут быть представлены в разных формах. Для механизмов с одной степенью вольности одна из самых простых форм уравнений получается на основе теоремы об изменении кинетической энергии : изменение кинетической энергии механизма на некотором перемещении равняется сумме работ всех сил, которые действуют на звенья механизма на этом самом перемещении. Данный закон подают в виде уравнения
где Т — кинетическая энергия механизма в произвольном положении; Т0 — кинетическая энергия механизма в положении, которое принимается за начальное; _ — сумма алгебраизма работ всех сил и моментов, которые прилагаются к механизму на некотором перемещении.
Работу осуществляют все активные силы и моменты и силы трения во всех кинематических парах механизма.
Уравнение движения в энергетической форме. Сведем все силы и моменты механизма с одной степенью вольности к одному звену возведения, то есть заменим рассматриваемый механизм его динамической моделью. Поскольку вся нагрузка, прилагаемая к модели, выражается возведенным моментом МЗВ, то правая часть уравнения (4.9) равняется
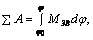
а именно уравнение (4.9), учитывая, можно записать в виде
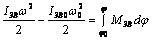
Уравнение (4.11) называют уравнением движения механизма в энергетическом виде, или — в форме уравнения кинетической энергии. В целом верхний предел _ интегрирования в (4.11) считается переменной.