5.Механизмы многозвенных зубчатых передач с неподвижными осями.
Механизмы трехзвенных зубчатых передач состоящие из двух сопряженных зубчатых колес, представляют собой простейший вид зубчатого механизма. часто приходится встречаться с необходимостью воспроизведения значительных передаточных отношений. Для осуществления этих передаточных отношений применяются несколько последовательно соединенных колес, где, кроме входного и выходного, имеются еще промежуточные колеса, т. е. многоступенчатые передачи. Такие сложные зубчатые механизмы получили название многоступенчатых передач или редукторов. Многоступенчатые передачи, у которых оси вращения колес неподвижны, носят также название рядового соединения. Передаточное отношение сложной многоступенчатой зубчатой передачи есть произведение взятых со своими знаками передаточных отношений отдельных его ступеней.
6.Профилирование кулачка. Силовой расчет кулачкового механизма.
А)Профилирование осуществляется на основе закона движения толкателя. В качестве примера рассмотрим профилирование кулачка в осевом механизме с поступательно движущимся толкателем. При этом дана схема механизма, диаграмма движения толкателя и rmin кулачка. В начале размечаются основные размеры механизма в масштабе , а также фазовые углы, причём углы делятся на ряд равных частей в соответствии с диаграммой. Строятся начальное, а затем ряд последующих положений толкателя в обращённом движении, и полученные точки соединяются плавной кривой.
*не знаю Б) Состовляется ряд уравнений : равновесия,Затем определяется реакция Заданной силы F. В основном работа с построенным рисунком.
7.Перманентное и начальное движение механизмов. Определение положений звеньев групп и постороннее траекторий описываемых точками звеньев механизма.
А)Перманентное
движение механизма т.е движение при
котором угловая скорость
кривошипа постоянна т.е
=const.
Б)Начальное движение- скорости всех звеньев мех-ма равны нулю.Для изучения этого движения мех-ма надо построить только план ускорений в начальном движении.
В)Для определения положения звеньев механизма должны быть заданы кинематическая схема мех-ма,и функция перемещений ведущего звена для мех-ма с одной степенью подвижности или фунцкции перемещения ведущих звеньев для мех - ма с несколькими степенями подвижности .Кинематическая схема должна быть построена в масштабе, что бы можно было измерить ее линейкой . Для построения траектории движения звеньев надо знать функцию перемещения ведущего звена.
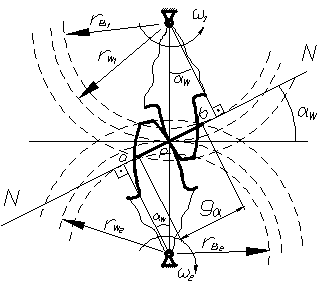
8.Геометрия плоских эвольвентных зубчатых механизмов.
В процессе зацепления зубья касаются друг друга различными точками профиля). Так как эти точки лежат на нормали к профилям, которая одновременно является касательной к обеим основным окружностям, то совокупность точек касания (линия ) совпадает с общей для обеих основных окружностей касательной NN. Эта линия называется теоретической линией зацепления, а линия длиной gα является её активной частью, где располагаются все точки контакта зубьев. Угол , измеряемый между нормалью NN к профилям в полюсе зацепления Р и общей касательной к обеим начальным окружностям, называется углом зацепления. Таким образом:
