5) Теорема Остроградского – Гаусса.

Определим поток напряжённости поля электрических зарядов через некоторую замкнутую поверхность, окружающую эти заряды. Рассмотрим сначала случай сферической поверхности радиуса R, окружающей один заряд, находящийся в ее центре (рис. 13.6). 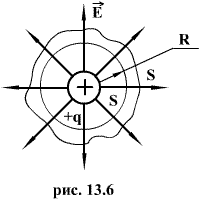  Напряженность поля по всей сфере одинакова и равна

Силовые линии направлены по радиусам, т.е. перпендикулярны поверхности сферы   , следовательно

т.к.    Тогда поток напряженности   будет равен

Используя формулу напряжённости, находим

(13.6)

Окружим теперь сферу произвольной замкнутой поверхностью S’. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно формула (13.6) справедлива не только для сферы, но и для любой замкнутой поверхности. Если произвольной поверхностью окружаем n зарядов, то очевидно, что поток напряженности через эту поверхность равен сумме потоков, создаваемых каждым из зарядов, т.е.

или

(13.7)

Таким образом, полный поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы численно равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности, поделенной на   . Это положение называется теоремой Остроградского - Гаусса. С помощью этой теоремы можно определить напряженность полей, создаваемых заряженными телами различной формы.

6) Электрическое поле равномерно заряженной плоской поверхности.

Если заряд распределён по поверхности, удобно пользоваться понятием поверхностной плотности заряда. Выделим на плоской поверхности малый участок площадью ΔS; пусть его заряд Δq. Тогда поверхностная плотность заряда равна σ =Δq/ΔS. Если заряд распределён равномерно, то σ =q/S.

Р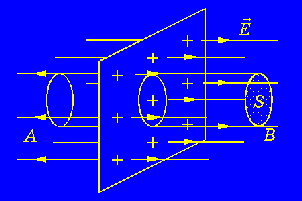 ассмотрим бесконечную равномерно заряженную плоскость. Её электрическое поле однородно, то есть его напряжённость одинакова на любом расстоянии от плоскости, линии напряжённости параллельны. Выделим цилиндр, перескающий плоскость, образующие которого параллельны силовым линиям (и перпендикулярны плоскости), а основания параллельны плоскости (и перпендикулярны силовым линиям). Поток через боковую поверхность цилиндра равен нулю, а через основания одинаков и равен N=2E_nS. Заряд внутри цилиндра равен σS. По теореме Гаусса:                    σS  2E_nS=4πk—, тогда                      ε             |σ|       |σ|                   2π|σ|  Е=2πk— = —— (в СИ) = —— (в СГСЭ).               ε     2ε₀ε                     ε

7) Электрическое поле равномерно заряженной цилиндрической поверхности.

Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).

Предположим, что полая цилиндрическая поверхность радиуса R заряжена с постоянной линейной плотностью   .

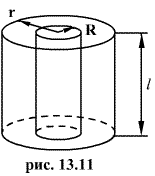
Проведем коаксиальную цилиндрическую поверхность радиуса   Поток вектора напряженности через эту поверхность

По теореме Гаусса

Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:

8) Электрическое поле равномерно заряженной сферической поверхности.

Рассмотрим электрическое поле равномерно заряженной сферы (полого тела, не шара). Поток напряжённости через любую замкнутую поверхность внутри сферы равен нуля, так как внутри этой поверхности нет заряда. Отсюда следует, что внутри сферы напряжённость равна нулю. Внутри себя равномерно заряженная сфера поля не создаёт.  E=0 при r<R.

И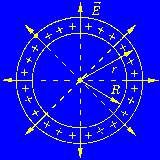 з соображений симметрии ясно, что вне сферы линии напряжённости направлены по радиусам. Напряжённость одинакова (по модулю) на одинаковом расстоянии от центра сферы. Проведём сферическую поверхность радиусом r>R. Поток напряжённости через неё равен N=E_nS=4πr²E_n. Пусть её заряд равен q. По теореме Гаусса:                        q  4πr²E_n=4πk—, тогда                        ε            |q|  Е=k—— при r>R.            εr²