41) Интерференция при отражении от тонких плёнок

Луч света, падающий на прозрачную пластинку, частично отражается и частично преломляется. Преломленный луч, отражаясь от нижней поверхности пластинки, идет к верхней и преломляется на ней второй раз. Таким образом получаются два луча.

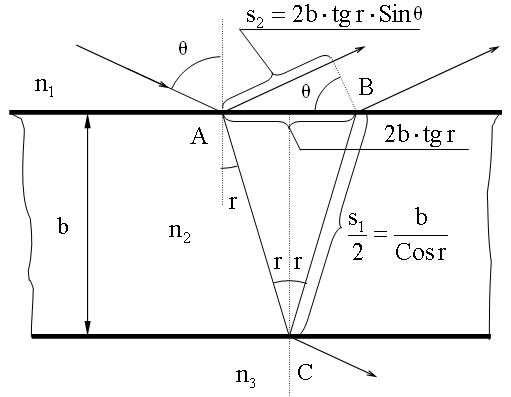
Если источник света естественный, то необходимым условием когерентности является малая толщина пластинок (интерференция в тонких пленках). При освещении лазерным лучом это ограничение отпадает.

При определении оптической разности хода необходимо учитывать изменение фазы отраженной волны на противоположную, если отражение происходит от оптически более плотной среды.

Для n₁ = 1 и n₃ > n₂ оптическая разность хода Δ = n₂S₂ - S₁. После преобразований с учетом закона преломления и тригонометрических формул получим:

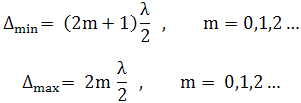
Если n₃ < n₂, тогда: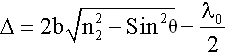 Здесь λ₀/2 появилась за счет изменения фазы волны на противоположную при отражении в точке A.

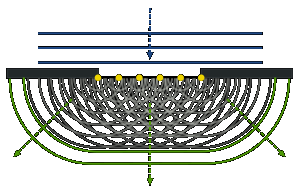
42) Кольца Ньютона

Плосковыпуклая линза большого радиуса кладется на стеклянную пластинку и освещается сверху параллельным пучком света. Так как радиус линзы R велик по сравнению с r - радиусом интерференционных полос, то угол падения света на внутреннюю поверхность линзы i ≈ 0. Тогда геометрическая разность хода с большой точностью равна 2b. 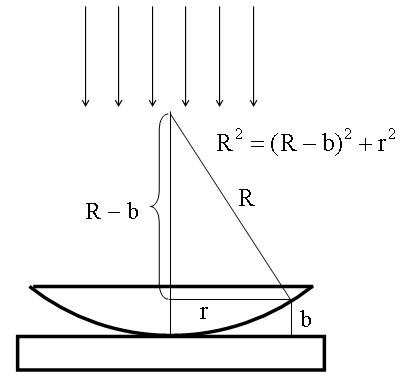При нахождении оптической разности хода следует учитывать изменение фазы на противоположную при отражении от оптически более плотной среды. Связь между b, r и R нетрудно найти из геометрических соображений.

max

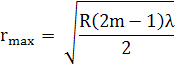
min

43) Дифракция света. Принцип Гюйгенса-Френеля

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий.

>Принцип Гюйгенса-Френеля

Каждая точка поверхности, достигнутая световой волной, является вторичным источником сферических световых волн. Огибающая вторичных волн становится фронтом волны в следующий момент времени.

44) Зоны Френеля

Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).

Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии от точки M (рис. 9.2). Точки сферы S, находящиеся на расстояниях , , и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.

Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M .

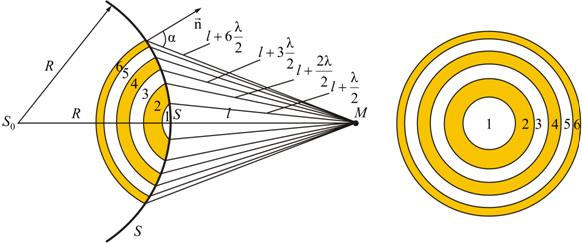
Рис. 9.2

Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга: , где A – амплитуда результирующего колебания, – амплитуда колебаний, возбуждаемая i-й зоной Френеля.

Величина зависит от площади зоны и угла между нормалью к поверхности и прямой, направленной в точку M.

Площадь одной зоны .

Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.

В то же время с увеличением номера зоны возрастает угол и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда . Она уменьшается также из-за увеличения расстояния до точки M: .

Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.

Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания от некоторой m-й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е. .

Результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной , а интенсивность .