31) Явление полного отражения

При переходе света из оптически более плотной среды в оптически менее плотную n₂ < n₁ (например, из стекла в воздух) можно наблюдать явление полного отражения, то есть исчезновение преломленного луча. Это явление наблюдается при углах падения, превышающих некоторый критический угол α_пр, который называется предельным углом полного внутреннего отражения (см. рис. 3.1.2).

Для угла падения α = α_пр sin β = 1; значение sin α_пр = n₂ / n₁ < 1.

Если второй средой является воздух (n₂ ≈ 1), то формулу удобно переписать в виде:

sin α_пр = 1 / n, где n = n₁ > 1 – абсолютный показатель преломления первой среды.

32) Оптическая система. Кардинальные плоскости

Оптическая система представляет собой совокупность отражающих и преломляющих поверхностей, отделяющих друг от друга оптически однородные среды.

Если лучи при своём отражении пересекаются в одной точке, то пучок называется гомоцентрическим.

Если система не нарушает гомоцентричности пучков, то лучи, вышедшие из точки Р пересекутся в точке Р’ и называются изображением.

S и S’ – сопряженные плоскости

Задней фокальной плоскостью F’ называется плоскость сопряженная с находящейся на бесконечности в пространстве плоскостью и перпендикулярной оси системы. Точка пересечения задней фокальной плоскости с осью системы называется задним фокусом системы.

Отношение линейных размеров изображения и предмета называется линейным или поперечным увеличением ( β ).

Существуют две такие сопряженные плоскости, которые отображают друг друга с линейным увеличением β =1. Эти плоскости называются главными. Точки пересечения главных плоскостей с осью системы называются главными фокусами.

Главные, фокальные и узловые плоскости называются кардинальными плоскостями. Задание кардинальных плоскостей точек полностью определяет свойства оптической системы.

33) Формула оптической системы

HF – переднее фокусное расстояние

H’F’ – заднее фокусное расстояние

Оптическая сила системы:

{Ф} = Дптр (Диоптрия)

- формула Ньютона

- x = - S – (- f) => x = S – f

x’ = S’ – f’

(S – f)(S’ – f’) = ff’

SS’ – fS’ – Sf’ + ff’ = ff’

SS’ = fS’ – Sf’

- формула оптической системы

34) Тонкая линза. Формула линзы

Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.

Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше (рис. 3.3.1).

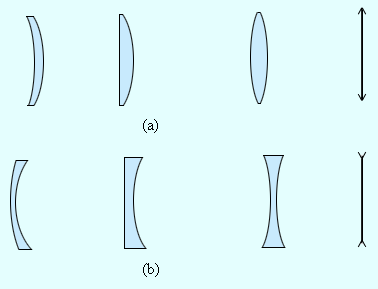
Рисунок 3.3.1.

Собирающие (a) и рассеивающие (b) линзы и их условные обозначения

Прямая, проходящая через центры кривизны O1 и O2 сферических поверхностей, называется главной оптической осью линзы. В случае тонких линз приближенно можно считать, что главная оптическая ось пересекается с линзой в одной точке, которую принято называть оптическим центром линзы O. Луч света проходит через оптический центр линзы, не отклоняется от первоначального направления. Все прямые, проходящие через оптический центр, называются побочными оптическими осями.

Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы. Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:

Величину D, обратную фокусному расстоянию, называют оптической силой линзы. Единицой измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = м^–1.