18. Порядковый подход к анализу полезности.

Ф.Эджуорд, В. Парето, И. Фишер, предложили альтернативный подход – порядковую теорию полезности. Она не предполагает, не только возможность и необходимость соизмерения полезности благ, но и вообще какое-либо упоминание о полезности.

. Достаточно лишь чтобы потребитель был способен упорядочить все возможные товарные наборы по их предпочтительности, при этом делается допущение, что потребители свободны в своих предпочтениях от доходов и цен.

Порядковый подход базируется на следующих аксиомах:

1. Аксиома полной (совершенной) упорядоченности (аксиома полноты):

пусть имеется два товарных набора А и В, тогда: либо А предпочтительнее В, А>В; либо В предпочтительнее А, В>А; либо товары А и В равноценны, А В.

2. Аксиома транзитивности (непротиворечивости потребительского выбора):

Пусть существует три товарных набора А, В и С. Известно, что А В и В>С, тогда А>С. Эта аксиома гарантирует согласованность предпочтений. В реальной жизни может оказаться наоборот: С>А. Это означает, что потребитель не имеет согласованных предпочтений. Можно предположить, что у него изменились вкусы. В теории же мы исходим из того, что вкусы неизменны в течение короткого промежутка времени.

3. Аксиома ненасыщения или понятие монотонности предпочтений: Если товарный набор А содержит не меньшее количества товара, чем В, а одного из них больше, то А>В.

4. Аксиома рефлексивности (оригинальности): все наборы данного вида одинаковы.

Пусть имеется товарный набор А(х₁,х₂,х₃) и товарный набор В(х₁,х₂,х₃), тогда А В.

5. Аксиома независимости потребителя: Удовлетворение потребителя зависит только от количества потребляемых им благ и не зависит от количества благ, потребляемых другими. Это означает, что потребителю незнакомы чувства зависти и сострадания.

19. Кривые безразличия.

Кривая безразличия – это линия, каждая точка которой представляет собой такой набор двух товаров, что потребителю безразлично, какой из этих товаров выбирать, т.к. каждый из них приносит один и тот же уровень удовлетворения (одинаковую полезность).

Т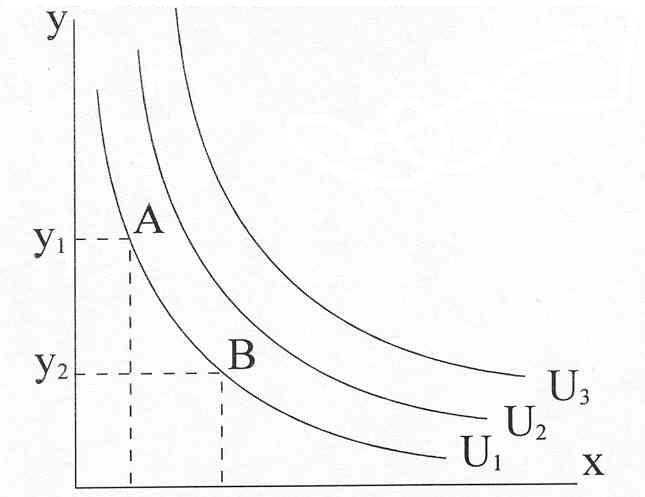 оварный набор А включает х₁ единиц товара Х и у₁ единиц товара У.

Товарный набор В(х₂, у₂).

Если с точки зрения данного потребителя наборы А и В равноценны, то точки А и В лежат на одной кривой безразличия.

Совокупность кривых безразличия называется картой безразличия.

Рис. 24.Кривые безразличия

Свойства кривых безразличия

1. Кривую безразличия можно провести практически через любую точку.

2. Кривая безразличия имеет отрицательный наклон.

3. Кривые безразличия никогда не пересекаются.

4. Кривые безразличия выпуклы в сторону начала координат.

5. Кривая безразличия, лежащая выше от начала координат, представляет собой более предпочтительные наборы товаров.

Если А В, E F, то AB<EF.

20.

Бюджетная линия. Равновесие потребителя.

Потребитель стремится приобрести товарный набор, принадлежащий наиболее удаленной от начала координат кривой безразличия, т.к. она представляет более предпочтительные наборы. Но потребитель ограничен в своих средствах, и далеко не всякий товарный набор ему доступен. Предположим, что потребитель тратит весь свой доход I на приобретение только двух товаров х и у, тогда бюджетное ограничение потребителя можно записать в виде:

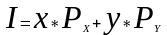
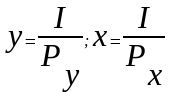где х и у – количество товаров х и у;

Р_х и Р_у – цены этих товаров.

Бюджетная линия демонстрирует все возможные комбинации товаров, которые доступны потребителю:

• Т

  Рис. 25. Бюджетная линия

  очка С свидетельствует о том, что потребитель часть дохода сберегает.

• Точка А демонстрирует недоступную потребителю комбинацию товаров.

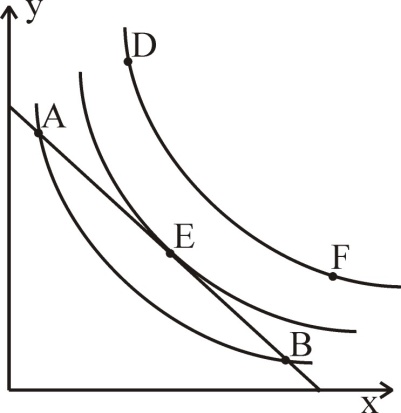
Е – потребительское равновесие.

Потребитель выберет точку Е, в которой бюджетная линия является касательной к кривой безразличия. Поскольку эта точка дает наибольшее возможное удовлетворение, то она и является точкой потребительского равновесия Е.

И1

Рис. 26. Равновесие потребителя

И3

И2