
2 Алгоритм работы программы
1)Программа начинается с того, что пользователь производит выбор объекта, по которому происходит построение моделей адаптивности.
2)По выбранному объекту производится ввод данных для построения моделей: коэффициентов объекта (a[i]), базовой точки(U0[i],i=1,2), интервалов покачивания(delta_U[i], i=1,2) и дисперсии помехи(Dh).
3)С помощью коэффициентов матрицы планирования переходим от безразмерных к экспериментальным координатам:
U(j)=(matrix_plan[i][j]+deltaU[j])+U0(j), i=1,N; j=1,2;
Полученные экспериментальные координаты подставляем в уравнение объекта и с учетом влияния помехи находим значения выхода объекта Y[i] i=1,N.
4) Расчитываем параметры модели. Безразмерные коэффициенты b[i] находятся по формуле:
b[j]=(x(j),Y)/N ,где Y-столбец измерений выхода объекта.
Далее производится переход от безразмерных координат b[i] к размерным а*[i]
5) Осуществляем проверку
модели на адекватность, для этого
необходимо найти остаточную дисперсию
(дисперсию адекватности). Вычисляем
остаточную сумму квадратов и делим ее
на число степеней свободы. Таким образом
получаем формулу для нахождения дисперсии
адекватности ( в ней Y[i] -
выход объекта в i-той
точке,
![]() [i]-
выход модели в i-той точке):
[i]-
выход модели в i-той точке):
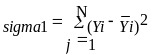
6) Находим оценку математического ожидания выхода модели. Затем найдем дисперсию выхода модели:
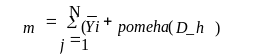
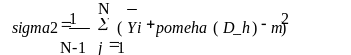
7)Теперь по статистике Фишера ( F=sigma1/sigma2) проверяем гипотезу о равенстве дисперсий, которая совпадает с гипотезой об адекватности модели. Если статистика F не превосходит порогового значения F(V1;V2;a), то принимается гипотеза об адекватности модели. В противоположном случае эта гипотеза отвергается, и модель считается неадекватной.
8) Вывод результатов вычислений на экран.
3 Результат работы программы:
1.Для линейного объекта.
Дисперсия Dh=1; Базовая точка (U1=0;U2=0); Интервалы покачивания (deltaU1=1;deltaU2=1); коэффициенты (a0=1;a1=1;a2=1;a12=1).
Результаты:
Для линейной модели:
a0=0.604; a1=0.858; a2=1.047 ;a12=0.704 ; модель адекватна
Для квадратичной модели:
a0=1.344; a1=0.118; a2=0.788; a12=0.333 ; а11=0.066; а22=0.017 ; модель адекватна
2) Меняем дисперсию помехи:
Дисперсия Dh=5; Базовая точка (U1=0;U2=0); Интервалы покачивания (deltaU1=1;deltaU2=1); коэффициенты (a0=1;a1=1;a2=1;a12=1).
Результаты:
Для линейной модели:
a0=2.350; a1=0.128; a2=-0.770 ;a12=-1.276 ; модель адекватна
Для квадратичной модели:
a0=-0.404; a1=0.884; a2=3.231 ;a12=0.589 ; а11=-0.640 ; а22=-1.688 ; модель адекватна
Меняем дисперсию помехи:
Дисперсия Dh=10; Базовая точка (U1=0;U2=0); Интервалы покачивания (deltaU1=1;deltaU2=1); коэффициенты (a0=1;a1=1;a2=1;a12=1).
Результаты:
Для линейной модели:
a0=-0.677; a1=-5.188; a2=9.777 ;a12=-3.201 ; модель адекватна
Для квадратичной модели:
a0=2.808; a1=-1.124; a2=2.062 ;a12=1.274 ; а11=2.534 ; а22=1.059 ; модель адекватна
Меняем базовую точку:
Дисперсия Dh=1; Базовая точка (U1=2;U2=3); Интервалы покачивания (deltaU1=1;deltaU2=1); коэффициенты (a0=1;a1=1;a2=1;a12=1).
Результаты:
Для линейной модели:
a0=12.012; a1=3.275; a2=2.373 ;a12=1.544 ; модель не адекватна
Для квадратичной модели:
a0=12.561; a1=2.927; a2=1.764 ;a12=0.542 ; а11=-0.215 ; а22=-0.126 ; модель не адекватна
Меняем базовую точку:
Дисперсия Dh=1; Базовая точка (U1=8;U2=8); Интервалы покачивания (deltaU1=1;deltaU2=1); коэффициенты (a0=1;a1=1;a2=1;a12=1).
Результаты:
Для линейной модели:
a0=81.789; a1=9.400; a2=8.904 ;a12=1.147 ; модель не адекватна
Для квадратичной модели:
a0=81.253; a1=6.146; a2=6.353 ;a12=0.286 ; а11=0.059 ; а22=-0.176 ; модель не адекватна
Меняем интервалы покачивания:
Дисперсия Dh=1; Базовая точка (U1=0;U2=0); Интервалы покачивания (deltaU1=4;deltaU2=4); коэффициенты (a0=1;a1=1;a2=1;a12=1).
Результаты:
Для линейной модели:
a0=0.544; a1=1.206; a2=1.010 ;a12=0.963 ; модель адекватна
Для квадратичной модели:
a0=0.466; a1=0.759; a2=0.688 ;a12=0.414 ; а11=0.019 ; а22=0.014 ; модель не адекватна
Меняем интервалы покачивания:
Дисперсия Dh=1; Базовая точка (U1=0;U2=0); Интервалы покачивания (deltaU1=10;deltaU2=10); коэффициенты (a0=1;a1=1;a2=1;a12=1).
Результаты:
Для линейной модели:
a0=0.661; a1=1.024; a2=1.066 ;a12=1.000 ; модель адекватна
Для квадратичной модели:
a0=1.193; a1=0.654; a2=0.651 ;a12=0.445 ; а11=-0.001 ; а22=0.004 ; модель не адекватна
2.Для квадратичного объекта.
Дисперсия Dh=1; Базовая точка (U1=0;U2=0); Интервалы покачивания (deltaU1=1;deltaU2=1); коэффициенты (a0=1;a1=1;a2=1;a12=1;а11=1;а22=1).
Результаты:
Для линейной модели:
a0=0.602; a1=0.155; a2=-0.201 ;a12=-0.556 ; модель адекватна
Для квадратичной модели:
a0=1.918; a1=-0.013; a2=-0.248; a12=-0.133 ; а11=0.025; а22=-0.032 ; модель адекватна
2) Меняем дисперсию помехи:
Дисперсия Dh=5; Базовая точка (U1=0;U2=0); Интервалы покачивания (deltaU1=1;deltaU2=1); коэффициенты (a0=1;a1=1;a2=1;a12=1;а11=1;а22=1).
Результаты:
Для линейной модели:
a0=2.429; a1=0.594; a2=-0.752 ;a12=-2.270 ; модель адекватна
Для квадратичной модели:
a0=4.265; a1=0.091; a2=-2.753 ;a12=-1.192 ; а11=0.992 ; а22=0.083 ; модель адекватна
3)Меняем дисперсию помехи:
Дисперсия Dh=10; Базовая точка (U1=0;U2=0); Интервалы покачивания (deltaU1=1;deltaU2=1); коэффициенты (a0=1;a1=1;a2=1;a12=1;а11=1;а22=1).
Результаты:
Для линейной модели:
a0=4.746; a1=-4.730; a2=-0.541 ;a12=0.526 ; модель адекватна
Для квадратичной модели:
a0=-1.556; a1=1.269; a2=0.983 ;a12=-2.879 ; а11=2.584 ; а22=-1.059 ; модель адекватна
Меняем базовую точку:
Дисперсия Dh=1; Базовая точка (U1=2;U2=3); Интервалы покачивания (deltaU1=1;deltaU2=1); коэффициенты (a0=1;a1=1;a2=1;a12=1;а11=1;а22=1).
Результаты:
Для линейной модели:
a0=10.728; a1=5.650; a2=-1.498 ;a12=-14.881 ; модель не адекватна
Для квадратичной модели:
a0=22.536; a1=2.571; a2=-1.233 ;a12=-3.095 ; а11=-1.512 ; а22=-1.572 ; модель не адекватна
Меняем базовую точку:
Дисперсия Dh=1; Базовая точка (U1=8;U2=8); Интервалы покачивания (deltaU1=1;deltaU2=1); коэффициенты (a0=1;a1=1;a2=1;a12=1;а11=1;а22=1).
Результаты:
Для линейной модели:
a0=147.644; a1=-39.963; a2=-39.280 ;a12=-68.935 ; модель не адекватна
Для квадратичной модели:
a0=178.994; a1=-8.420; a2=-10.091; a12=-29.541; а11=-11.872 ; а22=-10.258 ; модель не адекватна
Меняем интервалы покачивания:
Дисперсия Dh=1; Базовая точка (U1=0;U2=0); Интервалы покачивания (deltaU1=4;deltaU2=4); коэффициенты (a0=1;a1=1;a2=1;a12=1;а11=1;а22=1).
Результаты:
Для линейной модели:
a0=15.602; a1=-1.211; a2=-1.300 ;a12=-0.347 ; модель адекватна
Для квадратичной модели:
a0=18.029; a1=0.275; a2=0.207 ;a12=-0.147 ; а11=0.025 ; а22=0.021 ; модель не адекватна
Меняем интервалы покачивания:
Дисперсия Dh=1; Базовая точка (U1=0;U2=0); Интервалы покачивания (deltaU1=10;deltaU2=10); коэффициенты (a0=1;a1=1;a2=1;a12=1;а11=1;а22=1).
Результаты:
Для линейной модели:
a0=110.001; a1=-5.653; a2=-5.712 ;a12=0.044 ; модель не адекватна
Для квадратичной модели:
a0=96.800; a1=-1.630; a2=-1.592 ;a12=0.014 ; а11=0.080 ; а22=0.078 ; модель не адекватна
