Министерство Образования Российской Федерации

Красноярский Государственный Технический

Университет

Кафедра: Информатики Лабораторная работа №2 “Планирование эксперимента”

Выполнил: ст-т гр.АУ 61

Чебыкин М.А.

Проверил: Кузнецов А.В.

Красноярск 2003

1 Теоретические сведения.

Выход объекта состоит из сигнальной части, которая является функцией от входов и помехи, распределенной по нормальному закону:

Если представить функцию в виде ряда Тейлора в некоторой базовой точке (u₁⁰,u₂⁰), то модель можно построить в виде отрезка степенного ряда.

Если объект имеет два входа, то линейная статическая модель будет иметь вид:

Для нахождения коэффициентов ___ модели в вершинах прямоугольника задаем экспериментальные точки для входных координат, которые равномерно распределены относительно базовой вершины u⁰(u₁⁰,u₂⁰). Интервалы u₁,u₂ задаются экспериментатором. Далее осуществляется переход от размерных к безразмерным координатам.

Точки плана в вершинах прямоугольника оказываются в вершинах квадрата с единичными координатами. Центр плана переходит в начало координат. В новых координатах линейная модель имеет вид:

При планировании эксперимента у безразмерных координат принимающих значения +1 или –1 единицы опускаются и остается только знак. Условия эксперимента записываются в таблицы, в которых строки соответствуют различным опытам, а столбцы – значениям факторов. Такие таблицы называются матрицами планирования эксперимента. Для удобства в матрицу планирования вводят столбец фиктивной переменной x₀, которая во всех опытах принимает значение +1.

Коэффициенты  находятся по критерию наименьших квадратов

где у - столбец измерений выхода объекта, (х_j,у) – скалярные произведения столбцов матрицы планирования.

При построении модели выбирается точка u⁰(u₁⁰,u₂⁰), и интервалы покачивания, для имитации выходов задается дисперсия помехи ^. Строится план 1-ого порядка для построения линейной модели, количество точек плана равно 4. В каждой точке плана производится измерение выхода объекта.

Матрица планирования 1-ого порядка.

n	x0	х1	x2	y1….yn0
1	+	+	+
2	+	-	+
3	+	+	-
4	+	-	-

По полученным данным, используя математические ожидания выхода, строится линейная модель по всем точкам и находится дисперсия адекватности.

n=4 для линейного и n=9 квадратичного моделей, m=2

По статистике Фишера проверяется гипотеза о равенстве дисперсий, если гипотеза принимается, то модель адекватна, иначе строится модель второго порядка.

Для построения модели второго порядка доопределяются звездные точки, оптимальная длина звездного плеча  при m=2 равна 1.

Для того чтобы не нарушалась ортогональность плана все элементы каждого столбца x_j² изменяются на постоянную величину:

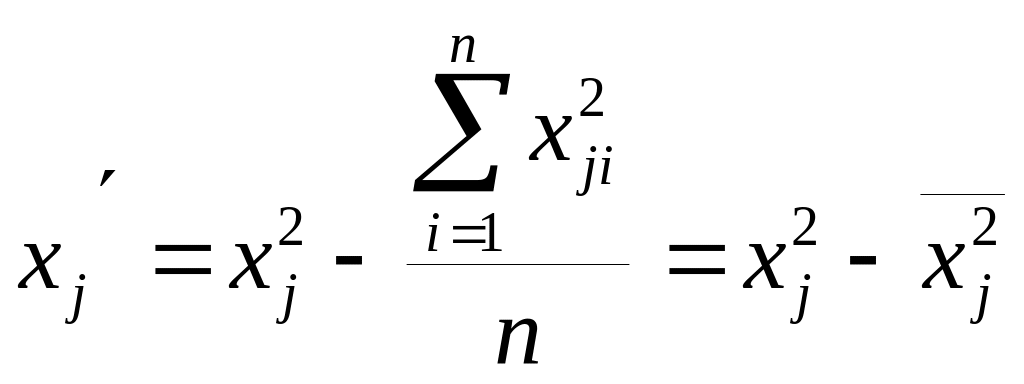
П ри =1

Матрица планирования 2-ого порядка

N	x0	х1	x2	x1x2	х1|	х2|	y1….yn0
1	+	+	+	+	1/3	1/3
2	+	-	+	-	1/3	1/3
3	+	+	-	-	1/3	1/3
4	+	-	-	+	1/3	1/3
5	+	+	0	0	1/3	-2/3
6	+	-	0	0	1/3	-2/3
7	+	0	+	0	-2/3	1/3
8	+	0	-	0	-2/3	1/3
9	+	0	0	0	-2/3	-2/3

С учетом новых переменных получаем следующее уравнение модели:

Где _^__вычисляются независимо, так же как при использовании ортогонального плана первого порядка.