6. Найімовірніше число появи випадкової події.

Найімовірнішим числом появи випадкової події А в результаті n незалежних експериментів за схемою Бернуллі називається таке чис­ло m₀, для якого ймовірність Р_n (m₀) перевищує або в усякому разі є не меншою за ймовірність кожного з решти можливих наслідків експериментів.

Для визначення найімовірнішого числа появи події немає потреби обчислювати ймовірності для різних можливих значень .

Формули для обчислення найімовірнішого числа появи випадкової події:

.

Число m₀ називають також модою.

_________________________________

6. Локальна теорема Лапласа.

Якщо ймовірність появи випадкової події в кожному з n незалеж­них експериментів є величиною сталою і дорівнює , то для великих значень n і m імовірність того, що випадкова подія А настане m раз, подається такою асимптотичною формулою:

,

де ℮

називається функцією Гаусса.

.

_________________________________

6. Інтегральна теорема Лапласа.

Якщо ймовірність появи випадкової події в кожному з n незалеж­них експериментів є величиною сталою і дорівнює , то для великих значень n імовірність появи випадкової події від m_і до m_j раз обчислюється за такою асимптотичною формулою:

,

де ,

а 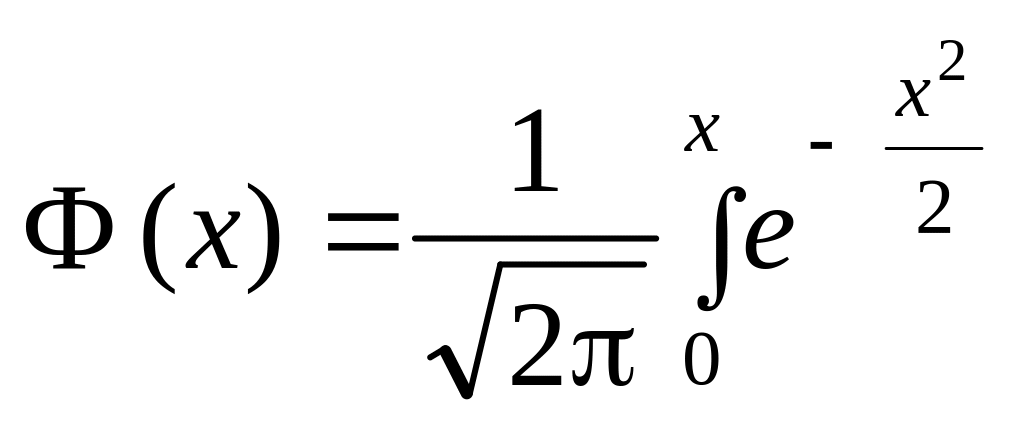є функцією Лапласа, значення якої наведено в таблиці.

___________________________________

6. Використання інтегральної теореми.

,

де ,

За допомогою цих формул можна оцінити близькість відносної частоти W(А) до ймовірності p випадкової події А. Нехай p — імовірність появи випадкової події А в кожному експерименті за схемою Бернул­лі й W(А) — відносна частота появи цієї події при n експериментах.

Необхідно оцінити ймовірність події W(A) – р<  ( > 0 і є малою величиною). Якщо n набуває великих значень, то можна дістати:

.

_________________________________

6. Формула Пуассона.

При за умови np=a= =const імовірність появи випадкової події m раз обчислюється за такою асимптотичною формулою:

,

яка називається формулою Пуассона.

Функція Р_n (m) визначається за таблицею за заданим m і обчисленим значенням а = np.

_________________________________

6. Дискретні та неперервні величини. Закони розподілу їх ймовірностей.

Розглянемо такий простір елементарних подій, в якому кожній елементарній події Ώ відповідає одне і лише одне число х або набір чисел , тобто на множині Ώ визначена певна функ­ція , яка кожній елементарній події ставить у відповідність певний елемент одновимірного простору R₁ або n-вимірного простору R_n.

Цю функцію називають випадковою величиною. У разі, коли відображає множину Ώ на одновимірний простір R₁, випадкову величину називають одновимірною. Якщо відображення здійснюється на R_n, то випадкову величину називають n-вимірною.

Величина називається випадковою, якщо внаслідок проведення експерименту під впливом випадкових факторів вона набуває того чи іншого можливого числового значення з певною ймовірністю. Якщо множина можливих значень випадкової величини є зчисленною то таку величину називають дискретною. У противному разі її називають неперервною.

Співвідношення, що встановляє зв’язок між можливими значеннями випадкової величини та відповідними їм імовірностями, називають законом розподілу випадкової величини.

Закони розподілу дискретних випадкових величин задаються у табличній формі, аналітичній, графічній. Універсальним способом задання закону розподілу ймовірностей є функція розподілу Для дискретних величин

_________________________________