ГУАП

КАФЕДРА № 52

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

				Тюрликов А.М.
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ

АНАЛИЗ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ИСПОЛЬЗОВАНИЕМ ДОСТУПА С РАЗДЕЛЕНИЕМ ПО ВРЕМЕНИ

по курсу: СИСТЕМЫ И СЕТИ СВЯЗИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР.	5921				Тигин Н.А.
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2012

1. Цель работы

2. Система массового обслуживания

3. Доступ с разделением по времени

4. Теоретическая оценка пустой системы

5. Пуассоновский входной поток

6. Асинхронная система массового обслуживания

7. Имитационное моделирование

8. Вычисление конечной теоретической оценки

1. Цель работы

Целью данной лабораторной работы является анализ системы массового обслуживания использующей доступ к каналу с разделением по времени. В ходе работы необходимо вывести теоретическую и практическую оценки задержки между появлением сообщения в системе и его отправкой.

2. Система массового обслуживания

В ходе лабораторной работы рассматривается система массового обслуживания (далее – СМО) обладающая следующими свойствами:

1. Система может обработать только одно сообщение в единицу времени

2. Сообщения поступают в систему по очереди с фиксированной интенсивностью λ

3. Среднее время обслуживания системы –

Для того, чтобы СМО имела конечную среднюю длину очереди, необходимо ограничить интенсивность входного потока , в противном случае очередь будет бесконечно возрастать.

Рис. 1 Система массового обслуживания

3. Доступ с разделением по времени

Система с данной моделью доступа описывается следующим образом:

1. В системе имеется фиксированное число абонентов N

2. Всё рабочее время системы разбито на окна; длина окна принимается за единицу времени; окна распределяются между абонентами

3. Каждый абонент генерирует сообщения в единицу времени с интенсивностью ; для генерации сообщений используется распределение Пуассона; сообщения сохраняются в очереди абонента

4. Абонент отправляет первое сообщение из очереди во время отведённого ему окна; при отсутствии сообщений в очереди абонента окно остаётся пустым

Для определения максимальной интенсивности входного потока необходимо рассмотреть СМО с использованием доступа с разделением по времени. Каждый абонент может отправлять сообщение в систему раз в N окон, а следовательно, система обрабатывает сообщение одного абонента N единиц времени. В таком случае, чтобы очередь была конечна, необходимо соблюдение неравенства , так как N, предельная интенсивность входного потока абонента , предельная интенсивность общего входного потока системы .

Работу системы можно представить в виде временной прямой разбитой на окна:

i

1. Окно принадлежащее i-тому абоненту

i.j

2. В очередь i-того абонента добавлено j-тое сообщение

i.j

3. j-тое сообщение i-того абонента вышло из системы в течении одного окна

Рис. 2 Использование доступа с разделением по времени

4. Теоретическая оценка пустой системы

Основной целью лабораторной работы является вычисление средней задержки между появлением сообщения в системе и его выходом из неё. Для упрощения оценки задержки рассмотрим пустую систему, т.е. систему, в которой отсутствуют сообщения в очереди. Кроме того, у абонента не может возникнуть более одного сообщения в очереди. Так как сообщение возникает в случайный момент времени, задержка представляет собой сумму трёх различных задержек.

1. Сообщение возникает в случайном интервале окна. Так как длина окна принята за единицу времени, сообщение ожидает конца окна от 0 до 1 ед. времени. Среднее время ожидания в таком случае составляет .

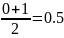2. Сообщение у абонента возникает в случайном окне. Рассмотрим 2 крайних случая.

   1. Сообщение возникло в окне абонента. В данном случае задержка составляет N-1 окон, так как время ожидания до границы текущего окна было учтено в первой задержке.

   2. Сообщение возникло в окне перед окном абонента. В данном случае требуется ждать 0 окон, так как время ожидания до границы текущего окна учтено первой задержкой.

Итого получается, среднее время второй задержки составляет .

3. На отправку сообщения абоненту требуется целое окно. Данная задержка не является вероятностной, следовательно она всегда будет равна 1.

При суммировании всех трёх задержек получается итоговая средняя задержка отправки сообщения: .