СОДЕРЖАНИЕ

1. Задача 1

1.1 Построение экономико-математической модели задачи……………..…..1

1.2 Построение матрицы модели……………………………………………….2

1.3 Решение задачи графическим методом…………………………………....3

1.4 Решение задачи симплексным методом…………………………………...3

1.5 Решение задачи на ПК в пакете SIMPLEX………………………………10

1.6 Решение задачи на ПК с помощью надстройки полок решения в среде EXCEL………………………………………………………………………......…10

2. Задача 2

2.2 Решение методом потенциалов. ………………………………………….13

2.3 Решение задачи в пакете PER……………………………………………..19

БИЬЛИОГРАФИЧЕСКИЙ СПИСОК…………………………………………20

Задача 1.

Цех выпускает установки двух видов. Для изготовления установок обоих видов используются переключатели, железо и проволока. Общий запас переключателей – 5000 шт., железа – 8 т, проволоки – 18 т. На одну установку первого вида расходуется 5 кг железа, 3 кг проволоки и устанавливаются 2 переключателя, а на одну установку второго вида расходуется 3 кг железа, 2 кг проволоки и устанавливается 1 переключатель. По плану необходимо произвести установок первого вида не менее 500 шт. За каждую реализованную установку первого вида завод получит прибыль 4 тыс.руб., второго – 1тыс.руб.

Составить план выпуска установок, обеспечивающий заводу максимальную прибыль.

Решение:

1. Построение экономико-математической модели задачи

1. Переменные.

Х1 – расход на установку первого вида, кг;

Х2 – расход на установку второго вида, кг.

2. Ограничения.

1. По наличию и использованию переключателей, шт

2Х1 + Х2 ≤ 5000

2) По наличию и использованию железа, кг

5Х1 + 3Х2 ≤ 8000

3) По наличию и использованию проволоки, кг

3Х1 + 2Х2 ≤ 18000

4) По производству установок первого вида, шт

Х1 ≥ 500

3. Целевая функция

Z = 4000Х1 + 1000Х2→ max

N ( 4000; 1000 )

Хj ≥0, j=(1,2)

1.2 Построение матрицы модели.

Таблица 1. Матрица модели.

п/п	Ограничения	Еден. измер.	Расход на установка первого вида	Расход на установку второго вида	Тип огр.	Объем огранич-я
			Х1	Х2
1	Поналичию и использованию переключателей	шт	2	1	≤	5000
2	По наличию и использованию железа	кг	5	3	≤	8000
3	По наличию и использованию проволоки	кг	3	2	≤	18000
4	По производству установок 1-го вида	шт	1	-	≥	500
Z	Максимизация	руб	4000	1000	→	max

1.3 Решение задачи графическим методом.

2 Х1 + Х2 ≤ 5000

5Х1+3 Х2 ≤ 8000

3Х1 +2 Х2 ≤ 1800

Х1 ≥ 500

Хj ≥0, j=(1,2)

Строим ограничения.

2Х1 + Х2 = 5000

5Х1+3 Х2 = 8000

3Х1 +2 Х2 = 18000

Х1 = 500

Далее построим графики граничных прямых (приложение А). Областью допустимых решений будет треугольник АВС. Построим вектор нормали (4000;1000). Максимум достигается в точке В( ). Значение целевой функции равно: Z=4000* + 1000* = 6400000 (руб.)

1.4 Решение задачи симплексным методом

2 Х₁ + Х₂ <= 5000

5 Х₁ + 13Х₂ <= 8000

3 Х₁ + 2 Х₂ <= 18000

Х₁ >= 500

Z = 4000*Х1 + 1000*Х2 => max

Предварительным шагом симплексного метода является приведение задачи к каноническому виду. Для этого в исходной задаче все основные ограничения приводятся к виду уравнений.

2 Х₁ + Х₂ + Х ₃ = 5000

5 Х₁ + 13Х₂ + = 8000

3 Х₁ + 2 Х₂ + = 18000

Х₁ - = 500

Х_j > 0 , ( j =1,6 )

Z = 4000*Х₁ + 1000*Х2­ + 0*Х3 + 0*Х4 + 0*Х5- 0*Х6 => max

Вспомогательная задача.

2 Х₁ + Х₂ + Х ₃ = 5000

5 Х₁ + 13Х₂ + = 8000

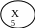
3 Х₁ + 2 Х₂ = 18000

Х₁ - Х6 + Х7 = =500

Х_j > 0 , ( j =1,7 )

Z = 4000*Х₁ + 1000*Х2­ + 0*Х3 + 0*Х4 + 0*Х5- 0*Х6 –M*Х7 => max

Итерация 1

Шаг 1

Выписываем исходное базисное решение и соответствующее ей значение целевой функции. На первой итерации в качестве базисных выбираем дополнительные переменные (в нашем примере это Х₃, Х₄, Х₅). Небазисные переменные Х₁ и Х₂ приравниваем к нулю.

Выписываем полностью исходное допустимое базисное решение:

Х₁ Х₂ Х₃ Х₄ Х₅ Х₆ Х₇

Х₁ =

0 0 5000 8000 18000 0 500

Z=4000*0 + 1000*0 + 0*5000 + 0* 8000 + 0*18000 – 0*0 – 500*М= – 500М

Шаг 2

Проверяем оптимальность полученного решения

Пусть : Δ Х₁ = 1

Тогда изменения для базисных переменных Х₃, Х₄, Х₅ запишутся так:

Δ Х₃ = - 2

Δ Х₄ = -5

Δ Х₅ = -3

Δ Х₇ = -1

Подставляя эти изменения значений переменных в целевую функцию, получим:

Δ Z = 4000 * 1 + 1000 * 0 + 0 * (-2) + 0 * (-5) + 0 * (-3) +0 *0 +(-1) * (-М) = 4000+ М > 0

Вывод: Решение Х₁ неоптимальное. Переменную Х₁ целесообразно ввести в базис, поскольку от этого значение целевой функции Z увеличится.

Шаг 3

Определяем, какая из прежних базисных переменных должна быть введена в базис и то уравнение, в котором это произойдет.

5000 : 2=2500

8000 : 5=1600

18000 : 3= 6000

500. : 1= 500 (*)

Вывод: Новая базисная переменная Х1 в четвертом уравнении, тогда прежняя Х7 будет выведена из базиса .

Шаг 4

Пересчет системы линейного уравнения с учетом нового состава базисных переменных.

Х₂ + - Х6 = 4000

3 Х₂ + = 5500

2 Х₂ + = 16500

- Х6 + Х7 = 500

Итерация 2

Шаг 1 Выписываем очередное допустимое базисное решение:

Х₁ Х₂ Х₃ Х₄ Х₅ Х₆ Х₇

Х₂ =

500 0 4000 5500 16500 0 0

и соответствующее ему значение целевой функции:

Z₂ = 4000*500+1000*0 +0*4000+0*5500+0*16500+0*0+0*0 = 2000000

ШАГ 2. Проверяем оптимальность полученного решения.

Пусть : Δ Х₂ = 1

Тогда изменения для базисных переменных Х₃, Х₄, Х₅ запишутся так:

Δ Х₃ = - 1

Δ Х₄ = -3

Δ Х₅ = -2

Подставляя эти изменения значений переменных в целевую функцию, получим:

Δ Z =4000 * 0 +1000 *1 +0 *(-1) + 0 *(-3) + 0*(-2) +0 *0 +0* 0 = 1000 > 0

Вывод: Решение Х₂ неоптимальное. Переменную Х₂ целесообразно ввести в базис, поскольку от этого значение целевой функции Z увеличится

ШАГ 3. Определяем, какая из прежних базисных переменных должна быть выведена из базиса.

4000:1=4000

5500: 3 = 1833 1 (*)

3

16500:2 = 8250

Меньшее значение получилось во втором уравнении. Это означает, что замена базисной переменной должна произойти во втором уравнении задачи.

Шаг 4.Пересчет системы линейного уравнения с учетом нового состава базисных переменных

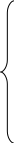
– 1 Х4 + 1 Х6 - 1 Х7 = 6500

3 6 3 3

+ 1 Х4 + 5 Х6 - 5 Х7 = 5500

3 3 3 3

2 Х4 + - 1 Х6 +1 Х7 = 38500

3 3 3 3

- Х6 + Х7 = 500

Итерация 3

Шаг 1 Выписываем очередное допустимое базисное решение

Х₁ Х₂ Х₃ Х₄ Х ₅ Х₆ Х ₇

Х₃ =

500 5500 6500 0 38500 0 0

3 3 3

и соответствующее ему значение целевой функции:

Z₃ =4000 * 500 + 1000 * 5500 +0* 6500+0*0+0*38500 +0*0+0*0=11500000 >0

3 3 3 3

Шаг 2 Проверяем оптимальность полученного решения

Пусть : Δ Х₆ = 1

Тогда изменения для базисных переменных Х₃, Х₄, Х₅ запишутся так:

Δ Х₃ = 1

3

Δ Х₂ = 5

3

Δ Х₅ = 1

3

Δ Х₁ = 1

Подставляя эти изменения значений переменных в целевую функцию, получим:

Δ Z =4000 *1 +1000 *( 5 ) +0*+ ( 1) + 0*0+0* 1 + 0*1+0*0=7000 > 0

3 3 3 3

Шаг 3

Определяем, какая из прежних базисных переменных должна быть выведена из базиса.

6500: 1 = 6500

3 3

5500 : 5 = 5500 = 1100 (*)

3 3 5

38500: ( 1) = - 38500

3 3

500: (-1)= -500

Шаг 4.Пересчет системы линейного уравнения с учетом нового состава базисных переменных

– 1 Х2 + + 6 Х4 = 1800

35 15

+ 3 Х2 + 1 Х4 - - Х7 = 1100

5 4

1 Х2 + - 7 Х4 + = 13200

4 12

3 Х2 +1 Х4 =1600

5 4

Итерация 4

Шаг 1 Выписываем очередное допустимое базисное решение

Х₁ Х₂ Х₃ Х₄ Х ₅ Х₆ Х ₇

Х₄ =

1600 0 1800 0 13200 1100 0

Z₃ =4000 * 1600+1000*0+*1800+0*0+13200*0+1100*0+0*0=6400000

Шаг 2.Проверяем оптимальность полученного решения

Пусть : Δ Х₆ = 1

Тогда изменения для базисных переменных Х₃, Х₄, Х₅ запишутся так:

Δ Х₄ = 1

Δ Х₃ = 6

15

Δ Х₆ = 1

4

Δ Х₅ = 7

12

Δ Х₁ = 1

4

Подставляя эти изменения значений переменных в целевую функцию, получим:

Δ Z = 4000* ( )+1000*0+0*

Вывод: Так как Δ Z<0, переменную Х_{4 нецелесообразно вводить в базис, поскольку значение} целевой функции от этого уменьшается.

Шаг 2 продолжается.

Пусть Х₂ = 1

Тогда Δ Х₃ =

Δ Х₅ =

Δ Х₁ =

Δ Х₆ = -

Δ Z = 4000* <0

Вывод: Так как Δ Z<0, переменную Х_{4 нецелесообразно вводить в базис, поскольку значение} целевой функции от этого уменьшается.

Общий вывод по шагу 2: Так как на данной итерации ни одну из базисных переменных нецелесообразно вводить в базис , решение Х_{4 является оптимальным.}

Экономический анализ решения

Так, по оптимальному плану необходимо произвести установок первого вида 1600 шт. что обеспечит заводу максимальную прибыль равную 6400000 руб.