14. Основные характеристики поведения функции

Изучить функцию – это значит охарактеризовать ход ее изменения (как говорят «ее поведение») при изменении независимой переменной. Для характеристики поведения функции используют следующие ее свойства. 1) ^ Четность функции. ОПРЕДЕЛЕНИЕ. Функция   называется четной, если выполняются два условия: а) область определения функции симметрична относительно начала координат; б) для любого   из области определения справедливо равенство  . ^ Функция   называется нечетной, если выполняются два условия: а) область определения функции симметрична относительно начала координат; б) для любого   из области определения справедливо равенство  . ^ Функция, не являющаяся четной или нечетной, называется функцией общего вида. Из определения четной и нечетной функции следует, что график четной функции симметричен относительно оси  , а график нечетной функции симметричен относительно начала координат. 2) Периодичность. ОПРЕДЕЛЕНИЕ. Функция  , определенная на множестве  , называется периодической, если существует число   такое, а) что для любого   значения   и   тоже принадлежат  ; б)  . Число   при этом называют периодом функции. Если функция   периодическая на множестве   и   на  , то для нее существует наименьший положительный период   и любой период этой функции имеет вид  , где   .   называют основным периодом функции  . Очевидно, что график периодической функции состоит из повторяющихся фрагментов. 3) Монотонность. ОПРЕДЕЛЕНИЕ. Функция   называется возрастающей (неубывающей) на интервале   если для любых   таких, что  значения функции   и   удовлетворяют неравенству   ( ). Функция   называется убывающей (невозрастающей) на интервале   если для любых   таких, что   значения функции   и   удовлетворяют неравенству   ( ). Возрастающие, убывающие, невозрастающие, неубывающие функции называются монотонными. 4) Ограниченность. ОПРЕДЕЛЕНИЕ. Функция   называется ограниченной снизу, если существует  ℝ такое, что  ,  . Функция   называется ограниченной сверху, если существует  ℝ такое, что  ,  . Функция, ограниченная сверху и снизу, называется ограниченной. Если функция   ограничена, то существует   такое, что  ,  .  Действительно, если   ограничена, то она ограничена сверху и снизу. Значит, существуют  ℝ такие, что  ,  . Обозначим через    ¹. Тогда   и  . Следовательно,  ,  , или  ,  .

1   обозначает наибольшее из чисел   и  .

15. Сложная Функция

математическая энциклопедия

- функция, представленная как композиция нескольких функций.

Источник: http://mirslovarei.com/content_matenc/slozhnaja-funkcija-100170.html#ixzz2IEdkFhG7

Обратная функция

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.

объясни на простейшем примере: у=2х+3 выразим х через у:  х=(у-3)/2 теперь заменим привычным образом:  у=(х-3)/2 функции у=2х+3 и у=(х-3)/2 - обратные. Их графики будут симетричны относительно прямой у=х. Кроме того область определения одной функции равна области значений другой функции. ЭТО СВОЙСТВА. теперь f(x)=2^(3x+1)  обратная f(x)=(log2_x - 1)/3 Логарифм по основанию 2 от х минус 1 и все это делить на 3.

16. В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел   или множества комплексных чисел  .

Пусть дано отображение  . Тогда его гра́фиком   называется множество       , где   обозначает декартово произведение множеств   и  .

• Графиком непрерывной функции   является кривая на двумерной плоскости.

• Графиком непрерывной функции 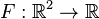  является поверхность в трёхмерном пространстве.

17.

18.