11) Геометрический смысл векторного произведения.
По определению длина векторного
произведения векторов равна
.
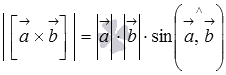А из курса геометрии средней школы нам
известно, что площадь треугольника
равна половине произведения длин двух
сторон треугольника на синус угла между
ними. Следовательно, длина векторного
произведения равна удвоенной площади
треугольника, имеющего сторонами векторы
и
,
если их отложить от одной точки. Другими
словами, длина векторного произведения
векторов
и
равна
площади параллелограмма со сторонами
и
и
углом между ними, равным
.
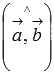В этом состоит геометрический смысл
векторного произведения.
12) Смешанное произведение трех векторов
Тройкой векторов
называются три вектора, если указано,
какой из них считается первым, какой
вторым и какой третьим. Тройку векторов
записывают в порядке нумерации; например,
запись
,
,
означает,
что вектор
считается
первым,
-
вторым,
-
третьим.
Смешанным произведением
трех векторов
,
,
называется
число, равное векторному произведению
,
умноженному скалярно на вектор
,
то есть
.
Имеет место тождество
,
ввиду чего для обозначения смешанного
произведения
употребляется
более простой символ
.
Таким образом,
,
.
Смешанное произведение равно объему параллелепипеда, построенного на векторах , , , взятого со знаком плюс, если тройка правая, и со знаком минус, если эта тройка левая. Если векторы , , компланарны (и только в этом случае), смешанное произведение равно нулю; иначе говоря, равенство
есть необходимое и достаточное условие компланарности векторов , , .
Если векторы , , заданы своими координатами:
,
,
,
то смешанное произведение определяется формулой
.
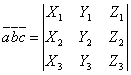13) Свойства смешанного произведения:
;
;
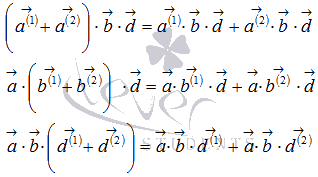
Очевидно, что если хотя бы один из умножаемых векторов нулевой, то смешанное произведение равно нулю.
Смешанное произведение также равно нулю, если хотя бы два умножаемых вектора равны.
Действительно, если
,
то по определению векторного произведения
,
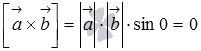следовательно, смешанное произведение
равно нулю, так как
.
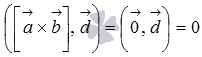Если же
или
,
то угол между векторами
и
равен
,
следовательно, по определению скалярного
произведения векторов
.
14) Геометрический смысл смешанного произведения.
Выясним геометрический смысл смешанного
произведения векторов
и
.
Отложим векторы и от одной точки и построим параллелепипед на этих векторах как на сторонах.
Обозначим
.
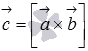В этом случае смешанное произведение
можно записать как
,
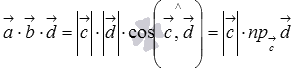где
-
числовая
проекция вектора
на
направление вектора
.
Абсолютная величина числовой проекции
равна
высоте параллелепипеда, построенного
на векторах
и
,
так как вектор
перпендикулярен
и вектору
и
вектору
по
определению векторного произведения.
А в разделе геометрический
смысл векторного произведения
мы выяснили, что величина
представляет
собой площадь параллелограмма,
построенного на векторах
и
.
Таким образом, модуль смешанного
произведения
-
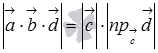это произведение площади основания на
высоту параллелепипеда, построенного
на векторах
и
.
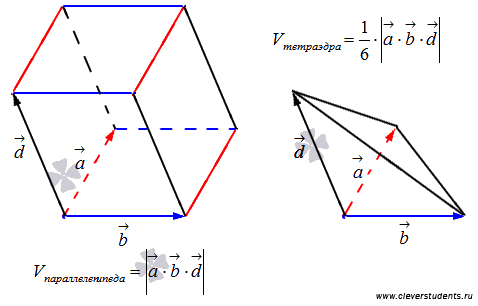
Следовательно, абсолютная величина
смешанного произведения векторов
представляет собой объем параллелепипеда:
.
В этом заключается геометрический смысл
смешанного произведения векторов.
Объем тетраэдра, построенного на векторах
и
,
равен одной шестой объема соответствующего
параллелепипеда, таким образом,
.
15)
Прямоугольная система координат
на плоскости образуется двумя взаимно
перпендикулярными осями координат
и
.
Оси координат пересекаются в точке
,
которая называется началом
координат, на каждой оси выбрано
положительное направление.
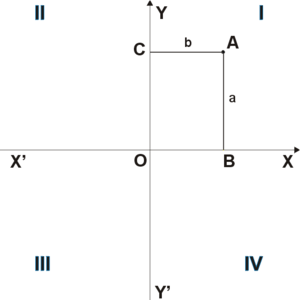
Рис. 1
Положение точки
на
плоскости определяется двумя координатами
и
.
Координата
равна
длине отрезка
,
координата
—
длине отрезка
в
выбранных единицах измерения. Отрезки
и
определяются
линиями, проведёнными из точки
параллельно
осям
и
соответственно.
При этом координате
приписывается
знак минус, если точка
лежит
на луче
(а
не на луче
,
как на рисунке). Координате
приписывается
знак минус, если точка
лежит
на луче
.
Таким образом,
и
являются
отрицательными направлениями осей
координат (каждая ось координат
рассматривается как числовая
ось).
Координата называется абсциссой точки , координата — ординатой точки .
Символически это записывают так:
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся
лучом, который называют нулевым или
полярной осью. Точка, из которой выходит
этот луч, называется началом координат
или полюсом. Любая точка на плоскости
определяется двумя полярными координатами:
радиальной и угловой. Радиальная
координата (обычно обозначается
)
соответствует расстоянию от точки до
начала координат. Угловая координата,
также называется полярным углом или
азимутом
и обозначается
,
равна углу, на который нужно повернуть
против часовой стрелки полярную ось
для того, чтобы попасть в эту точку.[1]
Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
