Билет 15

Расхождение между расчетным и действительным значением изучаемых величин, называют ошибкой наблюдения.

Для избегания ошибок:

1) Обеспечить качественное обучение персонала, проводящего наблюдение.

2) Организация специальной проверки правильности заполнения статистических формуляров.

3) Провести логический и арифметический контроль полученных данных после окончания сбора информации.

В зависимости от причин возникновения существуют ошибки репрезентативности и регистрации.

Ошибки регистрации - отклонения между значениями показателя, полученные в ходе статистического наблюдения и фактическим, действительным его значением.

Бывают случайными и систематическими.

Ошибки репрезентативности - отклонения значения показателя обследованной совокупности от его величины по исходной.

Бывают случайными (возникают, когда отобранная совокупность не полностью воспроизводит всю совокупность в целом); систематическими (появляются из-за нарушения принципов отбора единиц из исходной совокупности).

Билет 16

Способы отбора единиц в выборочную совокупность

Способ отбора определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности.

Для характеристики надежности выборочных показателей используют среднюю ошибку выборки.

При соблюдении принципа случайного отбора средняя ошибка выборки определяется прежде всего объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, всё более точно характеризуем всю генеральную совокупность.

Средняя ошибка выборки также зависит от степени варьирования изучаемого признака.

В практике выборочных исследований наибольшее распространение получили следующие виды выборки: собственно-случайная, механическая, типическая, серийная, комбинированная.

Для получения собственно случайной выборки генеральная совокупность строго подразделяется на единицы отбора, и затем в случайном повторном или бесповторном порядке отбирается достаточное число единиц.

Случайный порядок подобен жеребьевке. На практике он чаще всего применяется при использовании специальных таблиц случайных чисел.

Выборочная доля (w), или частость, определяется отношением числа единиц, обладающих изучаемым признаком т, к общему числу единиц выборочной совокупности n:

w = m / п.

При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:

• для средней количественного признака

;

• для доли (альтернативного признака)

.

При случайном бесповторном отборе в приведенные выше формулы расчета средних ошибок выборки необходимо подко­ренное выражение умножить на 1 - (п / N), поскольку в процес­се бесповторной выборки сокращается численность единиц ге­неральной совокупности. Следовательно, для бесповторной вы­борки расчетные формулы средней ошибки выборки примут такой вид:

для средней количественного признака

;

для доли (альтернативного признака)

При чисто механической выборке вся генеральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, составленного в каком-то нейтральном по отношению к изучаемому признаку порядке, например по алфавиту. Затем список единиц отбора разбивается на столько равных частей, сколько необходимо отобрать единиц. Далее по заранее установленному правилу, не связанному с вариацией исследуемого признака, из каждой части списка отбирается одна единица.

Для определения средней ошибки механической выборки используют формулы собственно-случайной бесповторной вы­борки.

При типической выборке до начала ее формирования генеральная совокупность единиц разбивается на типические группы. При этом очень важным моментом является правильный выбор группировочного признака. Отбор из каждой группы осуществляется в случайном порядке.

При определении средней ошибки типической выборки в ка­честве показателя вариации выступает средняя из внутригрупповых дисперсий.

для средней: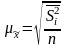 (повторный отбор);

(повторный отбор);

для доли: (бесповторный отбор); (бесповторный отбор);

Серийная выборка – это такой вид формирования выборочной совокупности, когда в случайном порядке отбираются не единицы, подлежащие обследованию, а группы единиц (серии, гнезда). Внутри отобранных серий (гнезд) обследованию подвергаются все единицы. 

Чаще всего применяется комбинирование способов отбора и видов выборки. Такие выборки получили название комбинированные. Комбинирование возможно в разных сочетаниях: механической и серийной выборки, типической и механической, серийной и собственно случайной и т. д. 

.

Среднюю ошибку выборки для средней при серийном отборе находят по формулам:

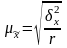(повторный отбор);

(повторный отбор);

где r - число отобранных серий; R - общее число серий.

Средняя ошибка выборки при серийном отборе:

(бесповторный отбор); (6.18) (бесповторный отбор);

Конечной целью выборочного наблюдения является ха­рактеристика генеральной совокупности на основе выбороч­ных результатов.

Билет 17

Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки. 

Предельную ошибку выборки для средней ( ) при повторном отборе можно рассчитать по формуле:

,

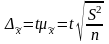где t— нормированное отклонение — «коэффициент доверия», за­висящий от вероятности, с которой гарантируется предельная ошибка выборки; — средняя ошибка выборки.

Аналогичным образом может быть записана формула пре­дельной ошибки выборки для доли при повторном отборе:

.

На основании теоремы П.Л. Чебышева (с уточ­нениями A.M. Ляпунова) с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом объеме выборки и ограниченной генеральной дисперсии выборочные обобщающие показатели (средняя, доля) будут сколь угодно мало отли­чаться от соответствующих генеральных показателей.

Применительно к нахождению среднего значения признака эта теорема может быть записана так:

,

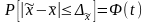а для доли признака:

,

где .

Таким образом, величина предельной ошибки выборки мо­жет быть установлена с определенной вероятностью.

Значения функции Ф (t) при различных значениях t как ко­эффициента кратности средней ошибки выборки, определяются на основе специально составленных таблиц.

Предельная ошибка выборки отвечает на вопрос о точности выборки с определенной вероятностью.

Предельная ошибка выборки позволяет определить предель­ные значения характеристик генеральной совокупности и их дове­рительные интервалы:

• для средней ; (6.25)

• для доли ; (6.26)

Это означает, что с заданной вероятностью можно утвер­ждать, что значение генеральной средней следует ожидать в пределах от до .

Аналогичным образом может быть записан доверительный интервал генеральной доли: ; .
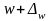