Билет 1

Определение статистики как науки

Статистика - общественная наука, которая изучает количественную сторону качественно определенных массовых социально-экономических явлений и процессов, их структуру и распределение, размещение в пространстве, движение во времени, причем в конкретных условиях места и времени.

Для изучения предмета статистики разработаны и применя­ются специфические приемы, совокупность которых образует методологию статистики (методы массовых наблюдений, груп­пировок, обобщающих показателей, динамических рядов, индексный метод и др.). Применение в статистике конкретных ме­тодов предопределяется поставленными задачами и зависит от характера исходной информации.

Статистические методы используются комплексно (системно). Это обусловлено сложностью процесса экономико-статистического исследования, состоящего из трех основных стадий:

первая – сбор первичной статистической информации;

вторая – статистическая сводка и обработка первичной информации;

третья – обобщение и интерпретация статистической информации.

На первой стадии статистического исследования, в связи с необходимостью учета всего многообразия фактов и форм осуществления социально-экономических процессов и в соответствии с их массовым характером, применяется метод массового статистического наблюдения, обеспечивающий все­общность, полноту и представительность (репрезентативность) полученной первичной информации.

На второй стадии – собранная в ходе массового на­блюдения информация подвергается обработке методом стати­стических группировок и таблиц, позволяющим выделить в изучаемой сово­купности социально-экономические типы; совершается переход от характеристики единичных фактов к характеристике данных, объединенных в группы величин.

Сводка - комплекс последовательных операций по обобщению конкретных, единичных фактов, образующих совокупность, для выявления типичных черт и закономерностей, присущих изучаемому явлению в целом.

Группировка - разбиение множества единиц изучаемой совокупности на группы по определенным, существенным для них признакам.

Методы группировки различа­ются в зависимости от задач исследования и качественного со­стояния первичного материала.

На третьей стадии проводится анализ статистиче­ской информации на основе применения обобщающих статисти­ческих показателей: абсолютных, относительных и средних ве­личин, вариации, тесноты связи и скорости изменения социаль­но-экономических явлений во времени, индексов и др. Прове­дение анализа позволяет проверить причинно-следственные свя­зи изучаемых явлений и процессов, определить влияние и взаи­модействия различных факторов, оценить эффективность при­нимаемых управленческих решений, возможные экономические и социальные последствия складывающихся ситуаций.

Билет 2

Статистическое наблюдение, совокупность

Статистическое наблюдение представляет собой научно организованный сбор сведений об изучаемом явлении или процессе.

1) Выбирается цель наблюдения - получение достоверной информации об изучаемом процессе или явлении.

2) Выбирается объект наблюдения - некоторая статистическая совокупность, в которой протекают исследуемые социально-экономические явления и процессы.

Статистическая совокупность- совокупность объектов и явлений, объединенных определенным признаком.

Выбирается единица наблюдения - составной элемент объекта наблюдения, который является носителем признаков, подлежащих регистрации в процессе наблюдения.

Отчетная единица - субъект, от которого поступают данные в процессе наблюдения.

Для определенного состава регистрируемых признаков разрабатывают программу наблюдения - перечень признаков или вопросов, подлежащих регистрации в процессе наблюдения.

Требования к программе наблюдения:

1) Программа должна содержать существенные признаки, непосредственно характеризующие изучаемое явление или процесс.

2) Вопросы программы должны быть точными и однозначными для понимания.

3) При разработке программы следует определять не только состав вопросов, но и их последовательность.

4) Целесообразно включать вопросы контрольного характера для проверки и уточнения собираемых данных.

5) Для обеспечения единообразия получаемых сведений от каждой отчетной единицы, программа оформляется в виде статистического формуляра - документа единого образца, содержащего программу и результаты наблюдения.

Формула состоит из 2 частей:

- титульная часть (содержит наименование статистического наблюдения, органа, проводящего наблюдение, информацию о том, кто и когда утвердил этот формуляр и иногда номер);

- адресная часть (содержит адрес единицы и ее подчиненность).

К формуляру прикладывается инструкция по его заполнению.

Выбор места наблюдения зависит от цели наблюдения, выбор времени заключается в решении 2 вопросов: установление критического момента (даты или интервала времени) и определении срока (периода) наблюдения.

Билет 3

Основные формы наблюдения:

-отчетность(бух баланс, отчет о прибылях и убытках)

-специально организованное наблюдение(перепись населения, соц. исследование);

-регистр (система, постоянно следящая за единицей наблюдения; организация и ведение регистра невозможно без решения следующих вопросов: когда заносить и исключать из него единицы совокупности, какая информация должна храниться, как часто она требует обновления; существуют регистры предприятий и населения).

Способы наблюдения:

-непосредственное наблюдение(инвентаризация на складе);

-документальный способ(изучение бухгалтерского баланса);

-опрос.

Виды наблюдения классифицируются по различным основаниям.

По времени регистрации фактов:

-текущее наблюдение( регистрация браков);

-периодическое наблюдение(перепись населения);

-единовременное наблюдение(перепись учреждений здравоохранения).

По степени охвата единиц совокупности:

-сплошное(перепись населения);

-несплошное (выборочное; метод основного массива; монографическое обследование)(структура грузооборота в деятельности фирмы).

Билет 4

Статистическая сводка — это комплекс последовательных операций по обобщению конкретных, единичных фактов, образующих совокупность, для выявления типичных черт и закономерностей, присущих изучаемому явлению в целом.

Статистическая группировка — это процесс образования од­нородных групп на основе расчленения статистической сово­купности на части или объединения изучаемых единиц в част­ные совокупности по существенным для них признакам, каждая из которых характеризуется системой статистических показате­лей.

Группировки по задачам, решаемым с их помощью, делятся на типологические, структурные и аналитические.

Типологические группировки - это разделение исследуемой, качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки.

Аналитическая группировка - группировка, которая выявляет взаимосвязи между изучаемыми явлениями и их признаками.

Особенности: в основу группировки кладется факторный признак; каждая выделенная группа характеризуется средними значениями результативного признака; группировка, в которой группы организованны по одному признаку называется простой, в которой группы разделены по двум и более признакам, взятым в сочетании называется сложной.

Билет 5

Виды статистических группировок

Группировки по задачам, решаемым с их помощью, делятся на типологические, структурные и аналитические.

Типологические группировки - это разделение исследуемой, качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки.

Аналитическая группировка - группировка, которая выявляет взаимосвязи между изучаемыми явлениями и их признаками.

Особенности: в основу группировки кладется факторный признак; каждая выделенная группа характеризуется средними значениями результативного признака; группировка, в которой группы организованны по одному признаку называется простой, в которой группы разделены по двум и более признакам, взятым в сочетании называется сложной.

Принципы построения статистических группировок.

Группировочным признаком называется признак, по которому производится разбивка единиц совокупности на отдельные группы. Называют его основанием группировки.

В основание группировки могут быть положены как количественные, так и качественные признаки.

Число групп, на которые необходимо разбить группировку определяется:

1) По формуле Стерджеса:

n=1+3,322lgN , где n-число единиц совокупности.

Хорошие результаты, если совокупность состоит из большого числа единиц и распределение единиц по признаку, положенному в основание группировки близко к нормальному.

2) Среднеквадратическое отклонение

ϐ= ,

Если величина интервала равна 0,5 ϐ, то совокупность разбивается на 12 групп. Если величина интервала 2/3 ϐ, то совокупность интервала разбивается на 9 групп. Если величина интервала равна ϐ, то совокупность интервала разбивают на 6 групп.

Билет 6

Виды интервалов группировок

Интервал - значение варьирующего признака, лежащее в определенных границах. Наименьшее значение - нижняя граница, наибольшее - верхняя граница. Разница межу верхней и нижней границей называется величиной интервала или интервальной разницей.

Существуют равные и неравные интервалы.

Равные интервалы - вариация признака проявляется в сравнительно узких границах, и распределение носит более или менее равномерный характер.

h= =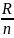

Правило определения шага интервала.

Если величина интервала, найденного по формуле, имеет один знак до запятой, то полученные значения округляют до десятых и используют в качестве шага интервала.

Если величина интервала имеет две цифры до запятой и несколько значений после, то округляют до целого числа.

Если величина представляет собой трех-, четырехзначную величину, то округляют до ближайшего числа, кратного 100 или 50.

Неравные интервалы. Могут быть прогрессивно возрастающими или убывающими в арифметической или геометрической прогрессии.

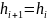= +q; *q

Неравные интервалы могут быть специализированными. Применяются для выделения из совокупности одних и тех же типов, по одному и тому же признаку, для явлений, находящихся в различных условиях.

Неравные интервалы могут быть произвольными. Применяются для изучения социально-экономических явлений на макроуровне.

Группировка с произвольными интервалами может быть построена с использованием коэффициента вариации.

= *100%

Построение групп этим методом начинается с упорядочивания единиц совокупности по возрастанию или убыванию группировочного признака. В полученном ряду значений признака, первые его значения объединяют в группу до тех пор, пока вычисленный для этой группы коэффициент вариации не станет равным 33%. Это свидетельствует об образовании первой группы. Затем эта группа исключается из исходной совокупности и алгоритм повторяется без этой совокупности до тех пор, пока все единицы совокупности не будут объединены в группы.

После определения группировочного признака и границ групп строится ряд распределения. Это упорядоченное распределение единиц совокупности на группы по определенному, варьирующему признаку.

Ряды распределения могут быть атрибутивными (ряды, построенные по качественным признакам, оформляются в виде таблиц) и вариационными (ряды, построенные по количественному признаку, состоят из вариантов - конкретное значение варьирующего признака и частот, сумма всех частот определяет численность совокупности или ее объем; в зависимости от характера вариации различают ряды дискретные и интервальные; дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, для графического изображения дискретных вариационных рядов используется кривая - полигон; построение интервальных вариационных рядов целесообразно при непрерывной вариации признака, либо если дискретная вариация в широких пределах; для изображения такого ряда используется гистограмма; для графического изображения вариационных рядов также используется кумулятивная кривая; если при графическом изображении ряда в виде кумуляты оси поменять местами, то получим огиву).

Билет 7

Относительные и абсолютные величины

Все абсолютные показатели являются именованными числами и выражаются в натуральных, стоимостных или трудовых единицах измерения.

Различают индивидуальные абсолютные величины, получают их непосредственно в процессе наблюдения как результат замера, подсчета, взвешивания и т.д.

Также выделяют сводные (объемные) показатели, они характеризуют объем признака или совокупности как в целом по объекту, так и по какой-либо его части. Получают их в результате сводки и группировки индивидуальных значений.

Относительные величины представляют собой результат деления одного абсолютного показателя на другой и выражают соотношение между количественными характеристиками социально-экономических процессов и при расчете абсолютный показатель, находящийся в числителе получаемого соотношения называют текущим или сравниваемым, а тот который находится в знаменателе называют основанием или базой сравнения.

Относительные показатели могут выражаться в %, коэффициентах или быть именованными числами.

Все относительные показатели делят на 7 видов.

1) Относительный показатель динамики:

ОПД=

Если данный показатель выражен кратным отношением, то он называется коэффициентом роста.

При умножении его на 100% получим темп роста.

2) Относительный показатель плана:

ОПП=

3) Относительный показатель реализации плана: ОПРП= _{показатель достигнутый в i-периоде/показатель запланированный в i-периоде}

4) Относительный показатель структур

ОПС=

5) Относительный показатель координации:

ОПК=

6) Относительный показатель интенсивности:

ОПИ=

7) Относительный показатель сравнения:

ОПСр=

Билет 8

Понятие о средних величинах

Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака, в расчете на единицу качественно однородной совокупности.

В каждом конкретном случае применяется одна из средних вели­чин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д.

Средняя арифметическая применяется в фор­ме простой средней и взвешенной средней. Исходной, опреде­ляющей формой, служит простая средняя.

Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеют­ся несгруппированные индивидуальные значения признака):

,

где x₁, x₂, …, x_n – индивидуальные значения варьирующего признака (варианты);

п ­– число единиц совокупности.

Средняя арифметическая взвешенная – средняя сгруппи­рованных величин x₁, x₂, …, x_n – вычисляется по формуле:

, (5.4)

где – веса (частоты повторения одинаковых признаков);

– сумма произведений величины признаков на их частоты;

– общая численность единиц совокупности.

Средняя гармоническая — сред­няя взвешенная из варьирующих обратных значений признака.

Когда статистическая информация не содержит частот по отдельным вариантам x совокупности, а представлена как их произведение , применяется формула средней гармониче­ской взвешенной, x*f=w.

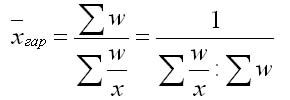
Средняя геометрическая исчисляется извлечением корня степени я из произведений отдельных значений — вариантов признака х.

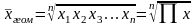
где п - число вариантов; П - знак произведения.

Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных зна­чений признака на их число:

;

Средняя квадратическая взвешенная

,

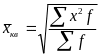где - веса.

Средняя кубическая простая

;

Средняя кубическая взвешенная

.

Билет 9

Структурные средние величины

Особым видом средних величин являются структурные сред­ние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Мода М_о — значение случайной величины, встречающее­ся с наибольшей вероятностью в дискретном вариационном ря­ду — вариант, имеющий наибольшую частоту.

В интервальных рядах распределения с равными интервала­ми мода вычисляется по формуле:

,

- нижняя граница модального интервала; - модальный интервал; ^— частоты в модальном, пре­дыдущем и следующем за модальным интервалах (соответственно). Модальный интервал определяется по наибольшей частоте.

Медиана М_е — это вариант, который находится в середи­не вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части — со значениями признака меньше медиа­ны и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое на­ходится в середине упорядоченного ряда.

В интервальных рядах распределения медианное значение (по­скольку оно делит всю совокупность на две равные по численно­сти части) оказывается в каком-то из интервалов признака х. Этот интервал характерен тем, что его накоп­ленная сумма частот равна или превышает полусумму всех час­тот ряда. Значение медианы вычисляется по формуле:

(5.17)

где - нижняя граница медианного интервала; 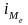- медианный интервал; - половина от общего числа наблюдений; сумма наблюдений, накопленная до начала медианного интервала;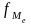 — число наблюдений в медианном интервале.

Мода и медиана, как правило, отличаются от значения сред­ней, совпадая с ней только в случае симметричного распределе­ния частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию ряда распределения.

Билет 10

Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному соче­таются в каждом отдельном случае.

Показатели вариации, характеризуют отклонения отдельных значений от общей средней.

К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.

Размах вариации R, представляющий собой разность между максимальным и минимальным значениями признака:

.

Однако размах вариации показывает лишь крайние отклоне­ния признака.

Среднее линейное отклонение d представляет собой сред­нюю арифметическую абсолютных значений отклонений отдель­ных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта: ( ).

Для несгруппированных данных , (5.18)

где n – число членов ряда;

Для сгруппированных данных , (5.19)

где — сумма частот вариационного ряда.

Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляет­ся по формулам простой и взвешенной дисперсий (в зависимо­сти от исходных данных):

• простая дисперсия для несгруппированных данных

,

• взвешенная дисперсия для вариационного ряда

.

Дисперсия позволяет оценить влияние различных факторов, обуславливающих вариацию признака; использование дисперсии для построения показателей тесноты корреляционной связи при оценке результатов выборочных наблюдений.

Среднее квадратическое отклонение — это обобщающая ха­рактеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные ва­рианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.

Среднее квадратическое отклонение равно корню квад­ратному из дисперсии:

• для несгруппированных данных

,

• для вариационного ряда

.

Билет 11

Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному соче­таются в каждом отдельном случае.

Показатели вариации, характеризуют отклонения отдельных значений от общей средней.

Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

Характеризует однородность совокупности. Совокупность считается количест­венно однородной, если коэффициент вариации не превышает 33 %.

Относительный размах вариации.Отражает относительную колеблемость крайних значений признака вокруг средней

Линейный коэффициент вариации характеризует долю усредненного значения абсолютного отклонения от средней величины. 

Билет 12

Виды дисперсий: обшей, меж­групповой и внутригрупповой, средняя из внутригрупповых.

Общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она может быть вычислена как простая дисперсия или взве­шенная дисперсия по формуле.

общая дисперсия для несгруппированных данных

,

взвешенная дисперсия для вариационного ряда

.

Межгрупповая дисперсия 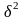характеризует систематиче­скую вариацию результативного признака, обусловленную влия­нием признака-фактора, положенного в основание группиров­ки. Она равна:

,

где - численность единиц в группе.

Внутригрупповая (частная) дисперсия отражает случай­ную вариацию, т.е. часть вариации, обусловленную влиянием не­учтенных факторов и не зависящую от признака-фактора, поло­женного в основание группировки.

Она равна:

;

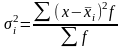
На основании внутригрупповой дисперсии по каждой груп­пе, т.е. на основании можно определить общую среднюю из внутригрупповых дисперсий :

.

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

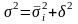
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью — неизвестную, а также судить о силе влияния группировочного признака.

Билет 13

Общая и межгрупповая дисперсия

Общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она может быть вычислена как простая дисперсия или взве­шенная дисперсия по формуле.

общая дисперсия для несгруппированных данных

,

взвешенная дисперсия для вариационного ряда

.

Межгрупповая дисперсия характеризует систематиче­скую вариацию результативного признака, обусловленную влия­нием признака-фактора, положенного в основание группиров­ки. Она равна:

,

где - численность единиц в группе.

Чем больше доля межгрупповой дисперсии в об­шей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак.

Поэтому в статистическом анализе широко используется

эмпирический коэффициент детерминации ( ) — показатель, пред­ставляющий собой долю межгрупповой дисперсии в общей дис­персии результативного признака и характеризующий силу влия­ния группировочного признака на образование общей вариации:

. (5.36)

Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть общей вариации у обуславливается вариацией прочих факторов).

Эмпирическое корреляционное отношение — это корень квад­ратный из эмпирического коэффициента детерминации:

,

оно показывает тесноту связи между группировочным и ре­зультативным признаками.

Эмпирическое корреляционное отношение , как и , может принимать значения 0 -1.

Чем значение корреляционного отношения ближе к еди­нице, тем теснее, ближе к функциональной зависимости связь между признаками.

Для качественной оценки тесноты связи на основе показате­ля эмпирического корреляционного отношения можно восполь­зоваться соотношениями Чэддока.

ηэ 0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99

Сила связи Слабая Умеренная Заметная Тесная Весьма тесная