Вопрос №1.

Основные понятия и определения ДУ:

Дифференциальным уравнением называется уравнение, связывающее независимую переменную x, искомую функцию у = у(х) и ее производ­ные у', у",..., т. е. уравнение вида

Если искомая функция у = у(х) есть функция одной независимой переменной дифференциальное уравнение называется обыкновенным например

F(x,y,y',y" у^{п)) = 0.

,

Когда искомая функция у есть функция двух и более независимых переменных, например если у = у(х, t), то уравнение вида

называется уравнением в частных производных. Здесь k,l — неотрица­тельные целые числа, такие, что k+l=m, например,

Порядком дифференциального уравнения называется порядок наивыс­шей производной, входящей в уравнение. Например, дифференциальное уравнение у' + ху = е^х — уравнение первого порядка, дифференциальное уравнение у" + р(х)у = 0, где р(х) — известная функция, — уравнение второго порядка; дифференциальное уравнение - ссу" = х² — урав­

нение 9-го порядка.

Решением дифференциального уравнения n-го порядка на интервале (а,b) называется функция у =φ(x), определенная на интервале (а,b) вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции у =φ(x) в дифференциальное уравнение

превращает последнее в тождество по х на (а, b). Например, функция у = sin x + cos x является решением уравнения у” + у = 0 на интервале (-оо, +оо). В самом деле, дифференцируя функцию дважды, будем иметь

у^’ = cos х - sin x, у" = - sin х - cos х.

Подставляя выражения у" и у в дифференциальное уравнение, получим тождество

• sin х - cos х + sin х + cos х = 0.

График решения дифференциального уравнения называется интегральной кривой этого уравнения.

Общий вид уравнения первого порядка

F(x, у, у') = 0. (1)

Если уравнение (1) удается разрешить относительно у', то получится

y’ = f(x, у) (2)

• уравнение первого порядка, разрешенное отно­сительно производной.

Множество касательных в каждой точке рассматриваемой области называется полем направлений.

С учетом сказанного выше можно привести следующее геометрическое истолкование дифференциального уравнения:

1) Задать дифференциальное уравнение первого порядка – это значит задать поле направлений.

2) Решить или проинтегрировать дифференциальное уравнение – это значит найти всевозможные кривые, у которых направление касательных в каждой точке совпадает с полем направлений.

Фазовое пространство – это пространство состояний движения точки по кривой.

Пусть дано к уравнений, связывающих независимую переменную х, к неизвестных функций у₁(х), у₂(х),…,у_к(х) и их производные различных порядков m₁, m₂,…,m_r . Требуется определить искомые функции так, чтобы они удовлетворяли одновременно всем заданным уравнениям. В этом случае говорят, что задана система из к  дифференциальных уравнений. Всякий раз предполагается, что число уравнений системы равно числу неизвестных функций. Случай, когда число уравнений меньше числа искомых функций (такие уравнения называются уравнениями Монжа) в данном пособии не рассматриваются. Предполагается также, что система может быть разрешена относительно старших производных, то есть, записана в виде

    (1)

Система (1) называется канонической. Каноническую систему (1) из к уравнений высших порядков можно заменить эквивалентною ей системой n=m₁+m₂+…+m_к уравнений первого порядка, разрешенных относительно производных всех n искомых функций. Для этого вводится новая система функций

 

Тогда получится система уравнений первого порядка. Чтобы не усложнять обозначения, пронумеруем вновь введенные функции по порядку у₁, у₂,…,у_n  и запишем систему

    (2)

Система n уравнений первого порядка вида (2) называется системой, имеющей нормальную форму Коши или нормальной системой обыкновенных дифференциальных уравнений. Функции f₁,f₂,…,f_n определены в некоторой области G  (n+1)- мерного пространства Rⁿ⁺¹.

Частным случаем канонической системы (2) является одно уравнение n-ого порядка, разрешенное относительно старшей производной

  . (3)

Переход к системе уравнений здесь осуществим введением новых функций:

   (4)

Можно говорить и обратное, то есть, что нормальная система (2) n уравнений первого порядка эквивалентна одному уравнению (3) порядка n. Действительно, если в системе (2) выбрать, например, первое из уравнений   и продифференцировать его n раз, всякий раз заменяя производные   через их правые части системы  , то получим одно уравнение порядка n:

 

Таким образом, решение нормальной системы уравнений может быть сведено к решению одного дифференциального уравнения и наоборот.

Вопрос № 2

Лемма Гронуолла

Задачей Коши называют задачу нахождения решения у = у(х) уравнения у' = f(x,y), удо­влетворяющего начальному условию у(хо) = уо (другая запись у|_х=_х0 = у₀).

Геометрически это означает, что ищется интегральная кривая, проходящая через задан­ную точку Мо(x0,y0) плоскости хОу (рис. 1).

Теорема существования и единственности решения задачи Ко­ши. Пусть дано дифференциальное уравнение y’ = f(x,y), где функция f(x,y) определена в некоторой области D плоскости хОу, содержащей точку (х₀, y0)• Если функция f(x, у) удовлетворяет условиям

а) f(x,y) есть непрерывная функция двух переменных х и у в области D ;

б) f(x, у) имеет частную производную , ограниченную в области D, то найдется интервал (x0-h, x0 + h), на котором существует единственное решение у = φ(х) данного уравнения, удовлетворяющее условию y(x0)=y0.

Вопрос №3

Определение 2.2. Решение ОДУ (2.1) непрерывно зависит от начальных условий, если для любого е > 0 существует такое 6(e) > 0, что при \хо — уо\ <6 для любого t € [to — h, to + h] будет выполнено неравенство |x(t) —y(t)| < e, где x(t) и y(t) — решения задач Коши в случае f_х = f₂ = f.

Определение 2.3. Решение задачи Коши непре­рывно зависит от правой части ОДУ (2.1), если для любого € > О существует такое δ(e) > 0, что при Δ< δ(e) для любого t [t0—h,to+h\ будет выполнено неравенство |x(t)-y(t)|<ε (здесь x(t) и у(<) — решения задач (2.13) Коши в случае хо=уо).

Предположим, что правая часть ОДУ зависит от параметра λ € Λ (Λ — некоторый отрезок числовой прямой |R):

(2.15)

a x(t, λ) — решение (2.15), удовлетворяющее начальному усло­вию

(2.16)

x(t0,λ)=x0.

Определение 2.4. Решение x(t, λ) задачи (2.15), (2.16) Коши непрерывно зависит от параметра λ, если для любого е > 0 существует δ(e) > 0, такое, что при всех |Δλ| < δ(e) для любого t € [to — h, <о + h] будет выполнено неравенство |x(t, λ + Δλ) — x(t, λ)| < е, где x(t, λ + Δλ) — решение задачи

15. , (2.16), соответствующее f(t,x, λ + Δλ) в правой час­ти (2.15).

Вопрос 4

????????????????????

Вопрос 5

имеем поле направлений, которое можно предста­вить на плоскости tOx, поместив в соотвествующих точках области D отрезки, образующие с координатной осью Ot углы arctg/(£, х). Это поле направлений можно представить также при помощи плоских кривых, описываемых уравнением /(£, х) = к (к = const) и называемых изоклинами

. Для ОДУ dx/dt = t² + x² уравнение изоклин имеет вид t² + х² = к, т.е. они представляют собой семейство концентрических окружностей радиуса

Вопрос 6

Обыкновенное дифференциальное уравнение (ОДУ) первого порядка вида

называют ОДУ с разделяющимися переменными. Будем предполагать, что функции f1(t),f2(x) непрерывны в ин­тервалах (t1,t2) и (а, 6) соответственно, и пусть При этих предположениях для ОДУ (3.1) в области

D = {(t,x): ti<t<t2, a<x<b}

выполнены условия теоремы Коши (см. замечание 2.2).

Умножив ОДУ (3.1) на dt/f₂{x), получим уравнение

(3.2)

в котором левая и правая части зависят от разных переменных. Преобразование (3.1) к виду (3.2) называют разделением пе­ременных.

Функция φ(t, х) является однородной функцией степе­ни k, если для всякого λ > 0 выполнено равенство φ(λt, λх) = λ^kφ(t, х). При к = 0 имеем φ(λt, λх) = λ^kφ(t, х). т.е. получаем однородную функцию нулевой степени.

Например, t² + х² — tx является однородной функцией второй степени, — однородной функцией k-й степе­ни, а (2t-x)/(t + x) — однородной функцией нулевой степени.

Обыкновенное дифференциальное уравнение (ОДУ) первого порядка

(3-7)

называют однородным, если f(t,x) — однородная функция нулевой степени (к = 0), т.е. f(λt, λх)=f(t,x). Если в этом равенстве положить λ = 1 /t, то получим тождество f(t,x) = f(1,x/t). Таким образом, если ОДУ (3.7) является одно­родным, то его правая часть будет функцией лишь одного аргумента x/t.

Обыкновенное дифференциальное уравнение (ОДУ) первого порядка dx/dt = f(t,x) иногда бывает удобно записать в форме

M(i, х) dt + N(t, х) dx = 0. (3.14)

В случае выполнения равенства <315>

тождественно (на всей плоскости tOx или в некоторой ее обла­сти D) (3.14) называют ОДУ в полных дифференциалах.

Если функции М(<, ж) и ЛГ(?, х) непрерывно дифференцируемы в некоторой области D, то условие (3.15) обеспечивает для любой точки (t0,x0)€D в некоторой ее окрестности существование такой функции W(t, ж), полный дифференциал

которой является левой частью (3.14), т.е.

M(t, x) dt + N(t, x)dx = dW(t, x). (3.16)

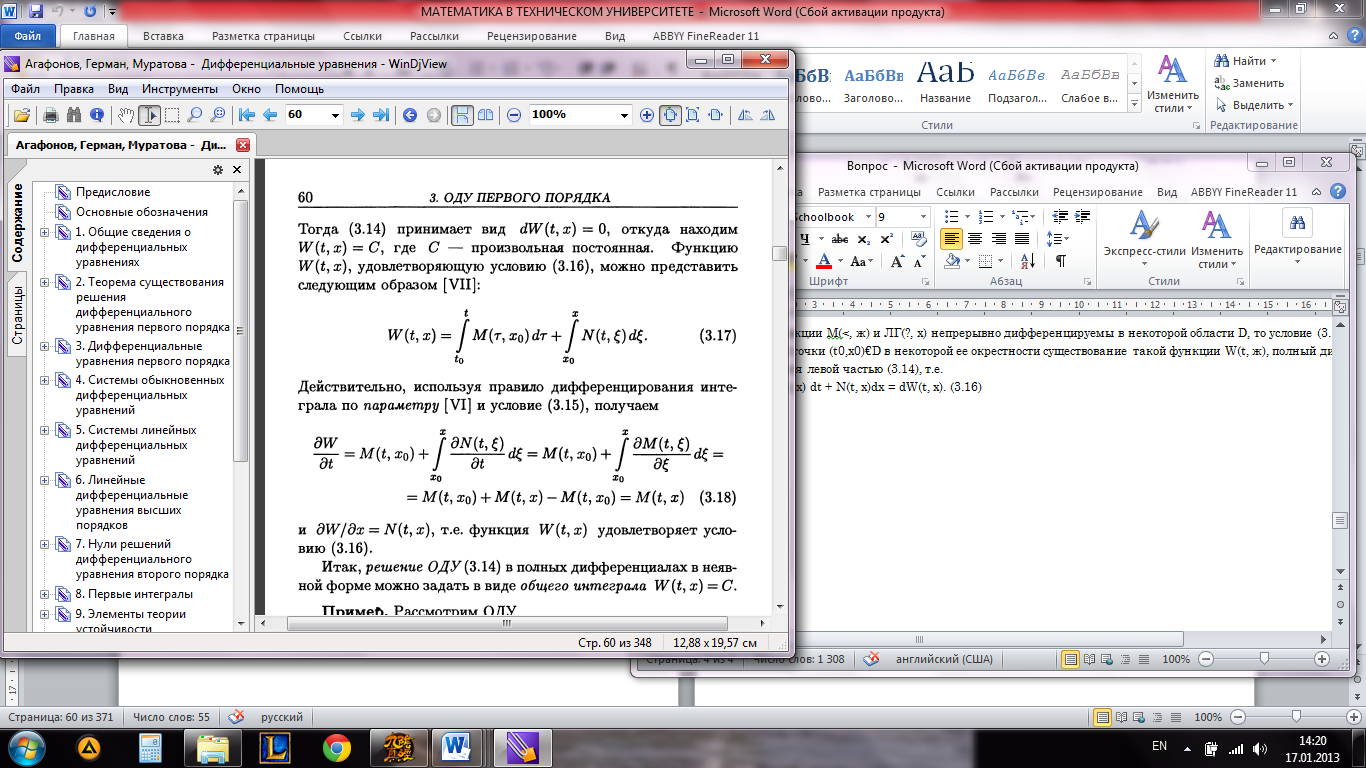
Вопрос 7

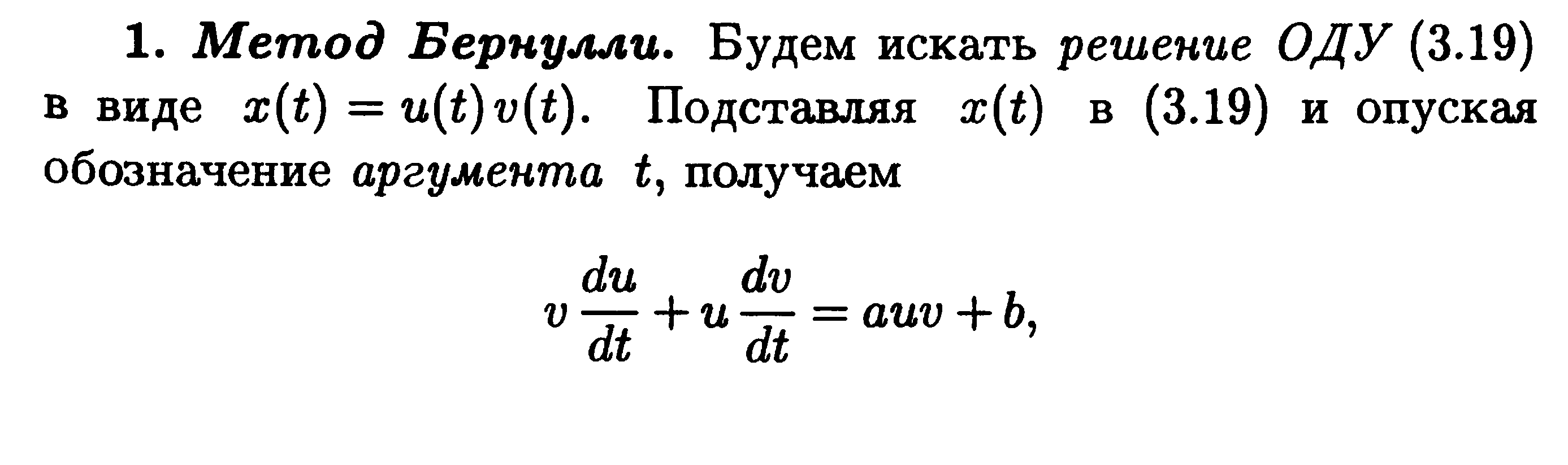
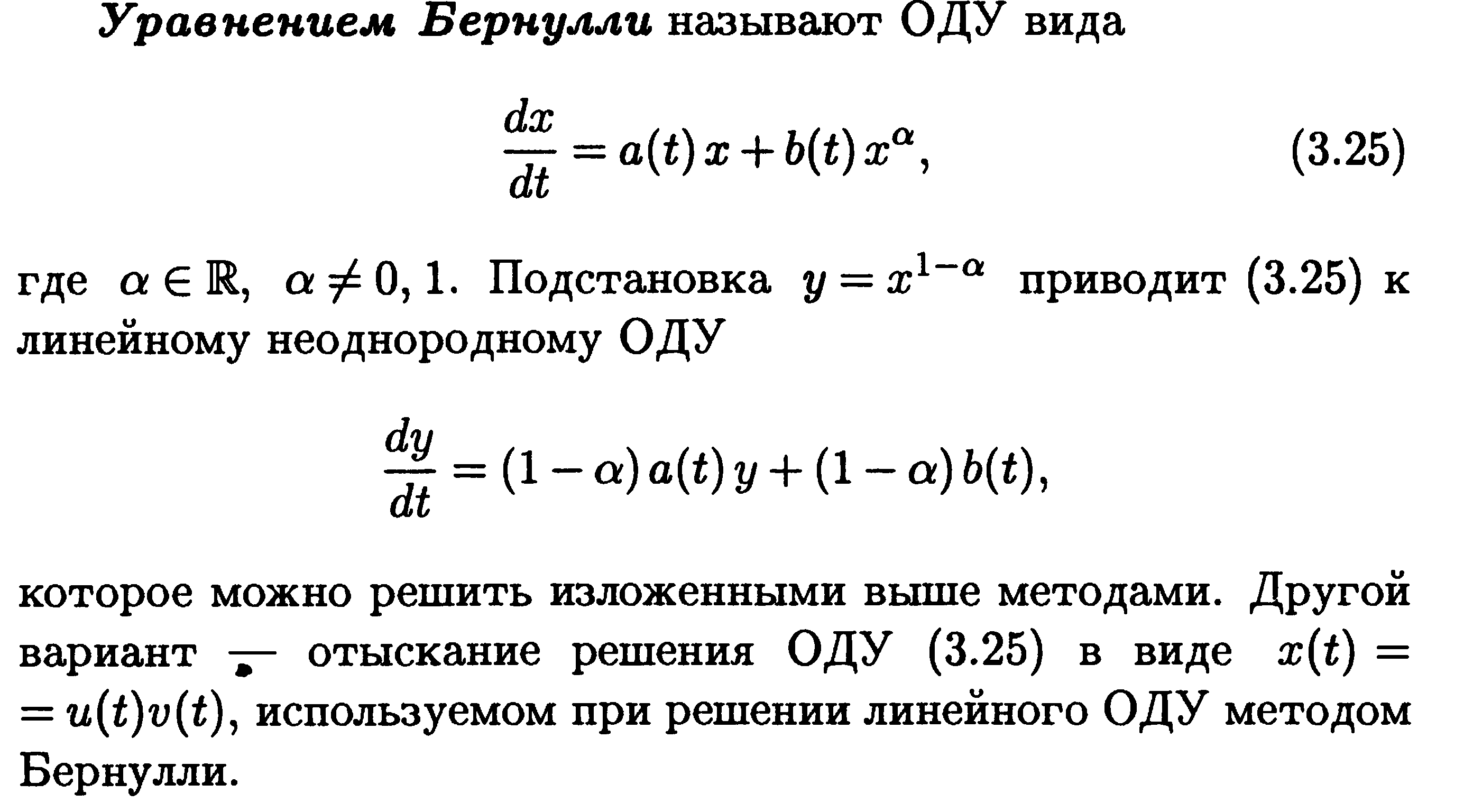
Вопрос №8

Вопрос № 9

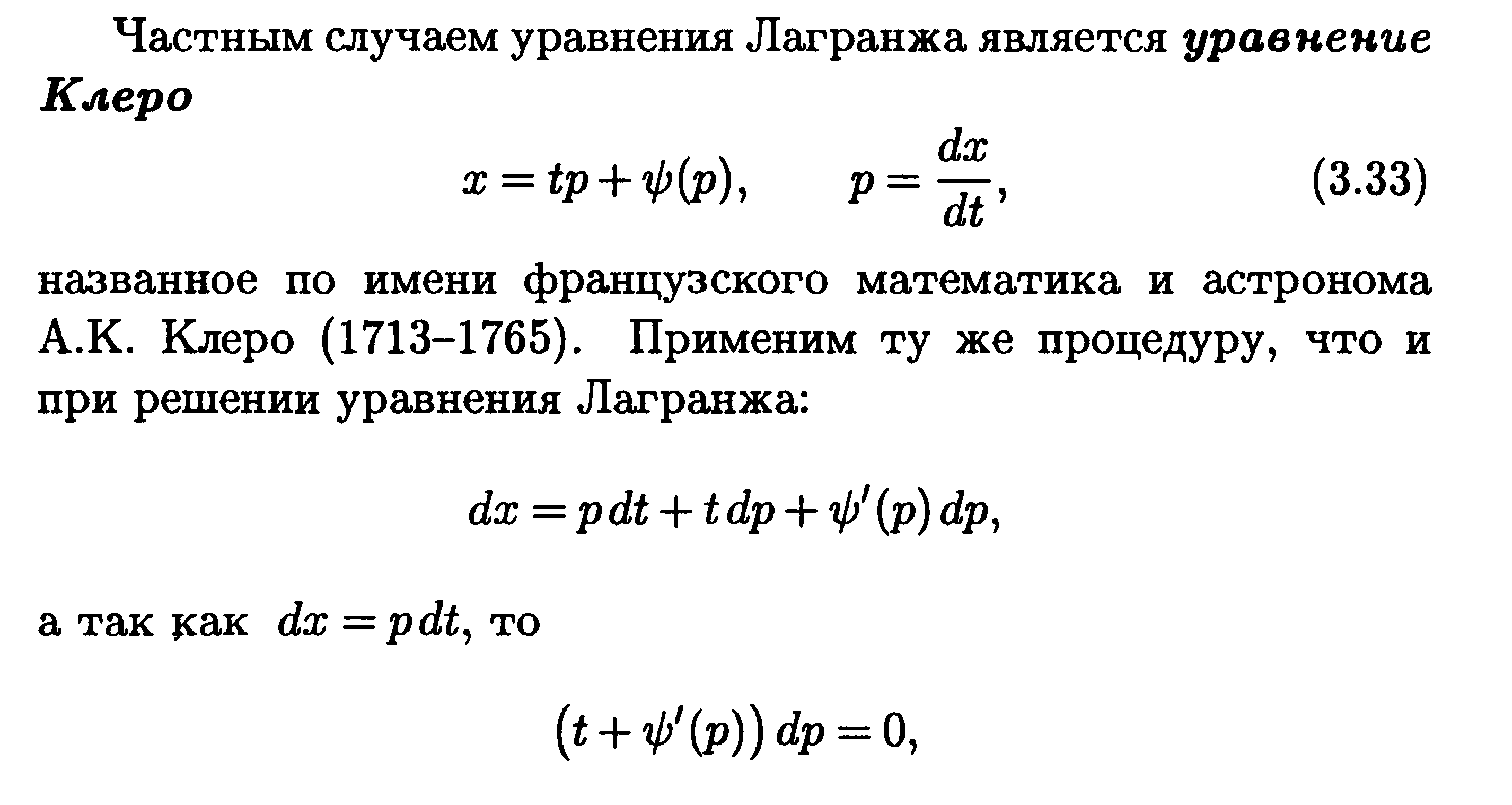
Вопрос №10

Вопрос №11

Вопрос 12

Вопрос 13

Вопрос № 14

6.5. Линейные дифференциальные уравнения второго порядка

Дифференциальное уравнение второго порядка имеет вид  . Определение. Общим решением уравнения второго порядка называется такая функция  , которая при любых значениях   и   является решением этого уравнения. Определение. Линейным однородным уравнением второго порядка называется уравнение  . Если коэффициенты   и   постоянны, т.е. не зависят от  , то это уравнение называют уравнением с постоянными коэффициентами и записывают его так:  . Уравнение   будем называть линейным неоднородным уравнением. Определение. Уравнение  , которое получается из линейного однородного уравнения заменой функции   единицей, а  и  - соответствующими степенями  , называется характеристическим уравнением. Известно, что квадратное уравнение   имеет решение, зависящее от дискриминанта  :  , т.е. если  , то корни   и  - действительные различные числа. Если  , то  . Если же  , т.е.  , то   будет мнимым числом, а корни   и  - комплексными числами. В этом случае условимся обозначать  .

Вопрос 15

?????????

Вопрос 16

Вопрос 17

Вопрос 18

Вопрос 18

Справедливо следующее утверждение ( теорема о структуре общего решения линейного однородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y₁(x),y₂(x),..., y_n(x) образуют фундаментальную систему решений этого уравнения, то общее решение уравнения имеет вид

y(x,C₁,..., C_n) = C₁ y₁(x) + C₂ y₂(x) + ... + C_n y_n(x),

где C₁,...,C_n — произвольные постоянные.

Впрос 19

Справедливо следующее утверждение ( теорема о структуре общего решения линейного неоднородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y₁(x),y₂(x),..., y_n(x) образуют фундаментальную систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид

y(x,C₁,..., C_n) = C₁ y₁(x) + C₂ y₂(x) + ... + C_n y_n(x) + y*(x),

где C₁,...,C_n — произвольные постоянные, y*(x) — частное решение неоднородного уравнения.