38. Вычисления определенных интегралов по отрезку [0,2п] от рациональной функции относительно sint и cost и несобственных интегралов с бесконечными пределами рациональных функций.
Рассмотрим интеграл вида
,
где
R(x) –
рациональная функция,
,
причем многочлен Q(x)
не обращается в нуль на вещественной
оси и его степень по крайней мере на две
единицы больше степени числителя. В
этом случае интеграл сходится и его
значение определяется по формуле
,
Вычисления определённых интегралов от тригонометрических функций
Пусть
функция
—
рациональная функция переменных
и
.
Для вычисления интегралов вида
удобно
использовать формулы Эйлера. Положив,
что
,
и произведя соответствующие преобразования,
получим:
.
39. Леммы Жордана. Несобственные интегралы по действительной оси от функций
(Лемма Жордана). Если f(z)C(Imz>0. z1,z2,...,zN) и f(z)=>0 при |z|(равномерно по argz , Imz>0), то при ReZ>0
CR
- полуокружность |z|=R
Imz>0.
Пусть R(x) - рациональная функция, не имеющая особых точек на действительной оси, для которой точка z, равная бесконечности, - нуль порядка не ниже первого.
Тогда
справедливы формулы:
40. Преобразование Лапласа. Условия на функцию - оригинал.
Пусть имеем функцию действительного переменного f(t), которая удовлетворяет следующим условиям:
1) f(t) однозначна и непрерывна вместе со своими производными n-го порядка для всех t, кроме тех, где она и ее производные имеют разрывы 1-го рода. При этом в каждом конечном интервале изменения t имеется конечное число точек разрыва;
2) f(t)=0для всех t<0;
3)
f(t)
возрастает медленнее некоторой
экспоненциальной функции
,
где М
и а-
некоторые положительные величины, т.е.
всегда можно указать такие М
и а,
чтобы при любом t>0
соблюдалось неравенство
.
В операционном исчислении функции f(t) ставится в соответствие новая функция F(p), определяемая равенством
Где p - положительное действительное число или комплексное число с положительной действительной частью.
Функция f(t) при этом называется оригиналом, а F(p)- изображением функции f(t) по Лапласу.
41 Теорема о существовании изображения и следствие из нее.
41* Второй метод исследования устойчивости Ляпунова. основные определения теории устойчивости. Т. об ассимптотичной устойчивости.
42 Изображения единичной функции, показательной, степенной, тригонометрических и гиперболических функций.
Нах-е изображения по оригиналу и наоборот наз-ся операц-м исчислением.
1.Ф-я
Хевисайда 1(t)=
F(p)=
=
,
Rep
;
1(t)
43 Линейность преобразования Лапласа, теоремы смещения и запаздывания
Линейность
-
Если f(t), g(t) -
функции-оригиналы, имеющие
изображения F(p), G(p),
то их линейная комбинация α f (t)
+ β g (t) (α =
cost, β =
const)- тоже функция-оригинал, и α f (t)
+ β g (t)
α F(p)
+ β G(p) .
ТЕОРЕМА
(смещения):Если
f(t)≑F(p),
то 
выполняется
f(t)≑F(p-
)
Смещение в области оригинала
Пусть f(t)- оригинал, тогда ф-я f(t-a) также яв-ся оригиналом с аргументом, запаздыв. на величину a. График ф-и f(t-a) не меняя своей формы получается из графика ф-и f(t) путем сдвига на a ед-ц вправо вдоль оси t.
ТЕОРЕМА
(запаздывания):
Пусть
F(t)
имеет изобр.F(p),
a>0,
тогда f(t-a)≑
44 Теорема подобия. Изображение периодического оригинала. Свертка оригиналов. Изображение свертки оригиналов
Если
f(t)≑F(p)
и
>0,
то f(λt)≑
Изображение периодического оригинала
ТЕОРЕМА:
Если f(t)-
оригинал с периодом T>0,
то F(p)=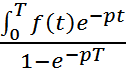
Изображение свертки оригиналов
Сверткой
2х ориг-в 
Так
при 
,
то для свертки получаем след. выр-е:
ТЕОРЕМА
(Борель):
Если
,
,то
Это равенство наз-ся ф-й умнож-я изоб-й
45 Дифференцирование и интегрирование оригинала и изображения
ТЕОРЕМА(Диф-е
оригинала): Если
оригинал и 
:если
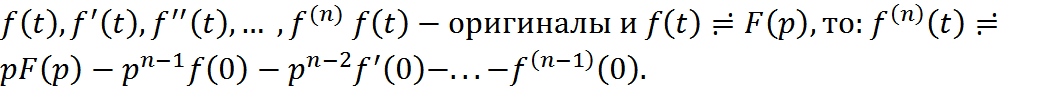
ТЕОРЕМА(Интегрирование оригинала):
Если
ТЕОРЕМА(Диф-ние изображения)
Если
ТЕОРЕМА(Интегрирование изображения)
Если
46 Обратное преобразование Лапласа (формула Меллина) Вторая теорема разложения
формула
Мелина
или обратное преобр-е Лапласа.
Интегрирование здесь ведется по любой
вертикальной прямой 
,
лежащей правее прямой 
,
т.к. 
; если F(p)-
удов-т
усл-м Леммы Жордана, то интеграл Меллина
м.б. вычислен с помощью вычета: 
2ая
теор. разлож-я.
47 Разложение для рациональных функций. Основная формула разложения.
Рас-им
случай, когда изображение F(p) пред-ет
собой правильную дробь 
; m < n, пусть 
корни
знаменателя кратности, 
соответственно (
),тогда
разложив знаменатель на множители можно
записать: 
т.е. P=pi
,
яв-ся полюсами порядка 
,
для ф-и F(p). Т.к. в это случае
основная формула разложения.
ТЕОРЕМА(разложения):Если
F(p)- анал-я ф-я в 
,
то 
и
ряд Лорана для F(p) имеет вид 
то оригиналом 
яв-ся ф-я 
сх-ся
при
t.