17 Фср лоду n-го порядка.
,
,
- const.
18 Лнду. Метод вариации произвольных постоянных.
если известно ФСР соот-его ЛОДУ 
.
Рас-им этот метод для ЛНДУ 2-го порядка
(1).
Пусть 
соот-его
ЛОДУ 
,
тогда общее решение ЛОДУ имеет вид 
.
Будем искать общее решение ЛНДУ в виде
схожем с этим общим реш-м, считая 
функ-ми от х, т.е. 
(2).
Наша задача – выбор ф-и 
,
т. о., чтобы ф-я (2) была реш-м ф-и (1). Усл-я
на ф-ии
подберем так, чтобы производная от ф-и
(2) имела такой же вид, как и при const
.
,
положим здесь: 
(3).
Тогда 
.
Поставим выражение для y,
y’
и y”
в ЛНДУ (1), и получим 
+
.
Перегруп-ем слаг-е 
)+
.
2-ая и 3-ья скобки последнего равенства
равны 0, т.к. 
ФСР ЛОДУ. Поэтому 
(4).
Объединим формулы (3) и (4) в систему
Главный
определитель системы 
-
ЛНФ-ии => система имеет един-ое реш-е.
Найдем реш-е системы по формулам Крамера
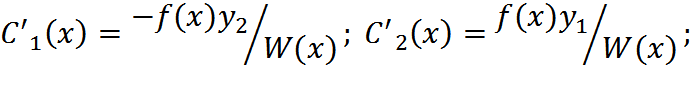Найдем
первообразные. Подставим найденные 
в формулу (2) и найдем общее реш-е ЛНДУ.
19 Структура общего решения лнду. Принцип суперпозиции решений.
ТЕОРЕМА:
Общее реш-е y
ЛНДУ пред-ет собой сумму общего реш-я
,
соот-его ЛОДУ и нек. частного реш-я ЛНДУ
y*,
т.е y=
+y*.
ТЕОРЕМА:
Принцип суперпозиции реш-й. Пусть 
-
реш-е ЛНДУ 
,
а 
-
реш-е ЛНДУ 
,
тогда y=
явл-ся
реш-м ЛНДУ 
.
20 Подбор частного решения лнду методом неопределенных коэффициентов
Правая часть ЛНДУ ф-ия f(x) может быть произвольной. В случае НДУ с пост-ми коэф-ми, когда правая часть в ур-и имеет вид
(1),
где α и β – const,
и 
- многочлены от x
n-ой
и m-ой
степени. Общее решение ЛНДУ y=
+y*,
где
-
общее реш-е ЛОДУ, y*
- частное реш-е ЛНДУ. Т.о. основная задача
заключ. в нах-и частного реш-я y*.
Y*
, когда правая часть ЛНДУ имеет вид (1),
а коэф-ты ур-я const,
ищется в виде 
,
где r-
показатель кратности корня 
харак-ого ур-я, 
– полные многочлены от x,
с неоп-ми коэф-и, причем l
равно наиб. из чисел n
и m.
Неопр-е коэф-ты можно найти из системы линейных алгебр-х ур-й, полученных отождествлением коэф-в при подобных членах в правой и левой частях исходного ур-я после подстановки в него y* вместо y.
21. Нор-ая система ДУ. Общее реш-е, з.Коши, частное реш-е. Геом. и механ. интерпретация системы 2-го порядка. Фазовая плоскость.
Норм-ой системой ДУ I порядка с m неизвестными ф-ми наз-ся система:
y’1 = f1 (x; y1; y2; …yn )
……………………….
y’n = fn (x; y1; y2; …yn )
З.Коши для системы доп-ся нач. усл-ми:
y1(x0) = y01
…………..
yn(x0) = y0n
ТЕОРЕМА (о сущ. и един. реш-я з.Коши)
Если
ф-и f1
…fn
непр-ны в окрестности т. М0(x0;y0;…y0n)
и имеют в этой точке непр. частные
производные 
, то найдётся интервал (x0
-
δ;
x0+
δ
,
на котором сущ. един. реш-е з.Коши.
Общим решением нормальной системы ур-ий яв-ся совокупность ф-й:
y1 = y1(x, C1, C2,…Cn)
…………………..
yn = yn(x, C1, C2,…Cn) каждая из которых зависит от n и const C1…Cn и удовл. усл-м:
1.Эти ф-и y1…yn яв-ся реш-ми системы при любых знач-ях произвольной const C1…Cn
2.Каковыми бы ни были нач. усл-я, найдутся такие значения C1…Cn, при которых эти ф-и удовл. данному нач. усл-ю.
Физ. смысл норм-ой системы.
Для простоты ограничимся рас-ем системы из 2 ур-й, причём независимую переменную t будем считать временем.
x’=f1(t,x,y)
y’=f2(t,x,y)
Реш-е x=φ(t); y=ψ(t) представляет собой некоторую кривую на плоскости OXY с фиксир. прямоуг-ой декартовой системой координат. Сама пл. OXY наз-ся фазовой пл-ю системы, а кривая яв-ся реш-ем системы, фазовой траекторией. Система наз-ся динамической. Динам. система яв-ся автономной, если в правую часть ур-й системы время t не входит явным образом. Динам. система опр. поле скоростей движ-ся точки в любой момент времени t. Реш-е динам. системы x=φ(t); y=ψ(t) опр. Ур-я дв-я точки. Они указ-т на положение точки в опр. момент времени t. Нач. усл-я задают положение точки в нач. м. вр. Реш-я системы также опр. траекторию движ. точки, будучи ур-ми данной кривой в параметр. форме.