20. Деление многочленов с остатком. Существование и единственность частного и остатка(без доказательства).

Если Р(х), Q(х), К(х) – такие многочлены, что Р(х)=Q(х)К(х), то говорят, что

многочлен Р(х) делится нацело на многочлен Q(х) или К(х).

Если многочлен степени n делится на многочлен степени m, то частным от

деления будет многочлен степени n-m и этот многочлен будет единственным.

21. Значение многочлена. Корень многочлена. Теорема Безу и ее важнейшее следствие.

Действительное число a называется корнем многочлена P_n (x), если P_n (a) = 0.

Теорема Безу.

Остаток от деления полинома Pn(x) на двучлен (x-a) равен значению этого полинома при x = a.

Пусть : Pn(x) – данный многочлен степени n , двучлен (x-a) - его делитель, Qn-1(x) – частное от деления Pn(x) на x-a (многочлен степени n-1 ) , R – остаток от деления ( R не содержит переменной x как делитель первой степени относительно x ).

Доказательство : Согласно правилу деления многочленов с остатком можно записать :

Pn (x) = (x-a)Qn-1(x) + R . Отсюда при x = a :

Pn (a) = (a-a)Qn-1 (a) + R =0*Qn-1(a)+R=

=0+R=R .

Значит , R = Pn (a) , т.е. остаток от деления полинома на

(x-a) равен значению этого

полинома при x=a , что и требовалось доказать .

Следствия

• Число a является корнем многочлена p(x) тогда и только тогда, когда p(x) делится без остатка на двучлен x − a.

• Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).

  • Пусть α — целый корень приведённого многочлена A(x) с целыми коэффициентами. Тогда для любого целого k число A(k) делится на α-k.

22. Схема Горнера (вывод формул).

Если то при делении f(x) на g(x) частное q(x) имеет вид

где Остаток r находится по формуле

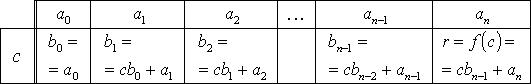
     Корни многочлена

     Корень многочлена f(x) - число , такое, что

     Число - k-кратный корень многочлена f(x), если

     Если число является k-кратным корнем многочлена f(x), то при k > 1 оно будет (k - 1)-кратным корнем первой производной этого многочлена; при k = 1 число не является корнем производной.

23. Рациональные корни многочленов с целыми коэффициентами.

Теорема о рациональных корнях многочлена

Если многочлен с целыми коэффициентами имеет рациональный корень то число p является делителем числа (свободного члена), а число q является делителем числа (старшего коэффициента).

Доказательство  

Действительно, если число является корнем многочлена то 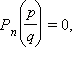а именно: Умножим обе части этого уравнения на получим: 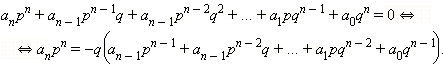Так как − целые числа, то в скобке стоит целое число. Значит, вся правая часть этого равенства делится на q , так как q входит в неё в качестве сомножителя. А значит и левая часть тождества делится на q , так как она равна правой. Число p не делится на q , так как иначе дробь была бы сократимой, значит и не делится на q . Следовательно, на q делится единственный из оставшихся сомножителей левой части, а именно Аналогично доказывается, что делится на p . Теорема доказана.