
- •Вопросы к экзамену
- •2 Курс/1cеместр
- •1.Определение предела функции в точке. Предел суммы, произведения, частного двух функций (с доказательством для суммы).
- •2.Определение производной, ее геометрический и физический смысл.
- •3.Определение касательной к графику функции. Вывод уравнения касательной к графику функции.
- •4.Теорема о непрерывности дифференцируемой функции.
- •5.Производная суммы, произведения, частного двух функций
- •Понятие сложной функции. Правило вычисления производной сложной функции.
- •Теоремы Ролля и Лагранжа(без доказательства).
- •Определение монотонной функции. Достаточное условие монотонности функции на промежутке.
- •Определение экстремума функции. Необходимое условие экстремума функции (теорема Ферма).
- •Достаточное условие экстремума функции.
- •Наибольшее и наименьшее значения функции на отрезке (теорема Вейерштрасса - без доказательства).
- •12. Асимптоты (вертикальные, наклонные) графика функции, вывод правила их нахождения.
- •Наклонная
- •13. Определение комплексных чисел. Алгебраическая форма записи комплексного числа. Модуль, сопряженные комплексные числа.
- •14. Операции над комплексными числами в алгебраической форме и их свойства. Действия над комплексными числами
- •15. Геометрическая интерпретация комплексных чисел. Геометрический смысл операций сложения и вычитания.
- •16. Тригонометрическая форма записи комплексного числа. Умножение и деление комплексных чисел, записанных в тригонометрической форме. Геометрический смысл умножения комплексных чисел.
- •17. Возведение комплексного числа в п-ю степень. Формула Муавра.
- •18. Определение комплексного корня п-й степени из комплексного числа. Формула корней из комплексного числа. Геометрический смысл комплексных корней п-й степени из единицы.
- •19. Многочлены от одной переменной. Степень многочлена. Равные многочлены. Основные свойства операций сложения и умножения многочленов.
- •20. Деление многочленов с остатком. Существование и единственность частного и остатка(без доказательства).
- •21. Значение многочлена. Корень многочлена. Теорема Безу и ее важнейшее следствие.
- •22. Схема Горнера (вывод формул).
- •23. Рациональные корни многочленов с целыми коэффициентами.
- •24.Обобщенная теорема Виета для многочлена п-й степени(без доказательства).
- •Формулировка
- •Векторы в пространстве. Сумма и разность векторов, умножение вектора на число. Коллинеарные векторы. Компланарные векторы. Угол между векторами.
- •Прямоугольная система координат в пространстве. Координаты точки. Координаты вектора. Вычисление расстояния между точками.
- •3.Вывод формул для координат точки, делящей отрезок в заданном отношении.
- •Уравнение плоскости, проходящей через заданную точку ортогонально заданному вектору.
- •6. Общее уравнение плоскости. Геометрический смысл коэффициентов общего уравнения плоскости.
- •7. Уравнение плоскости в отрезках.
- •8. Определение угла между плоскостями. Формула вычисления косинуса угла между плоскостями с выводом.
- •9. Параметрические уравнения прямой.
- •Уравнения прямой, проходящей через заданную точку параллельно заданному ненулевому вектору (канонические уравнения).
- •15. Условие перпендикулярности прямой и плоскости.
- •16. Определение угла между прямой и плоскостью. Вывод формулы вычисления синуса угла между прямой и плоскостью.
- •17. Вычисление координат точки пересечения прямой с плоскостью.
- •18. Определение расстояния от точки до плоскости. Вывод формулы вычисления расстояния от точки до плоскости.
- •20. Пересечение сферы с плоскостью.
3.Определение касательной к графику функции. Вывод уравнения касательной к графику функции.
Касательной
прямой к графику функции f в точке
x0 называется график линейной
функции, задаваемой уравнением
![]()
Рассмотрим кривую, уравнение
которой есть y=f(x). Возьмем на этой
кривой точку M(x0, y0),
и составим уравнение касательной к
данной кривой в точке M, предполагая,
что эта касательная не п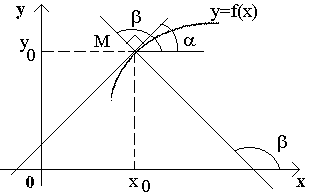 араллельна
оси Oy.
араллельна
оси Oy.
Уравнение прямой с угловым коэффициентом в общем виде есть у=kx + b. Поскольку для касательной k= f'(x0), то получаем уравнение y= f'(x0)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x0, y0). Поэтому ее координаты должны удовлетворять уравнению касательной: y0= f'(x0)·x0 + b. Отсюда b=y0– f'(x0)·x0.
Таким образом, получаем уравнение касательной y= f'(x0)·x +y0 – f'(x0)·x0 или
-
y = f '(x0)·(x – x0) + f(x0)
4.Теорема о непрерывности дифференцируемой функции.
Функция y=f(x) называется
дифференцируемой в некоторой точке
x0, если она имеет в этой точке
определенную производную, т.е. если
предел отношения
![]() существует
и конечен.
существует
и конечен.
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом, из дифференцируемости функции следует ее непрерывность.
Доказательство. Если
![]() ,
то
,
то
![]() ,
,
где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда
Δy=f '(x0) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x0)→0 при x→x0, а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать.
Таким образом, в точках разрыва функция не может иметь производной.
5.Производная суммы, произведения, частного двух функций
Пусть u=u(x), v=v(x) – две дифференцируемые функции от переменной x.
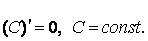
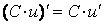 .
.
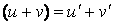 (справедлива
для любого конечного числа слагаемых).
(справедлива
для любого конечного числа слагаемых).
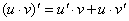 .
.
 .
.
а)
![]() .
.
б)
![]() .
.
Доказательство формулы 3.
Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx).
Тогда
Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv.
Следовательно,
![]() .
.
Понятие сложной функции. Правило вычисления производной сложной функции.
Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Областью определения функции y = f(u(x)) является либо вся область определения функции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области определения функции y= f(u).
Теорема. Если функция u=
u(x) имеет в некоторой точке x0
производную
![]() ,
а функция y= f(u) имеет в точке u0
производную y 'u= f '(u0),
то сложная функция y = f(u(x)) в указанной
точке x0 тоже имеет
производную, которая равна y 'x=
f '(u0)·u '(x0),
где вместо u должно быть подставлено
выражение u= u(x).
,
а функция y= f(u) имеет в точке u0
производную y 'u= f '(u0),
то сложная функция y = f(u(x)) в указанной
точке x0 тоже имеет
производную, которая равна y 'x=
f '(u0)·u '(x0),
где вместо u должно быть подставлено
выражение u= u(x).
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной.
Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y 'x осуществляется последовательным применением предыдущей теоремы.
По доказанному правилу имеем
y 'x= y 'u·u 'x
. Применяя эту же теорему для u 'x
получаем
![]() ,
т.е.
,
т.е.
y 'x = f 'u (u)·u 'v (v)·v 'x (x).
